RegionMeasure

RegionMeasure[reg]

領域 reg の測度を与える．

RegionMeasure[reg,d]

領域 reg の d 次元測度を与える．

RegionMeasure[{x1,…,xn},{{t1,a1,b1},…,{tk,ak,bk}}]

直交座標 xiが tjの関数であるパラメトリック式の k 測度を与える．

RegionMeasure[{x1,…,xn},{{t1,a1,b1},…,{tk,ak,bk}},chart]

xiを指定された座標チャートにおける座標として解釈する．

詳細とオプション

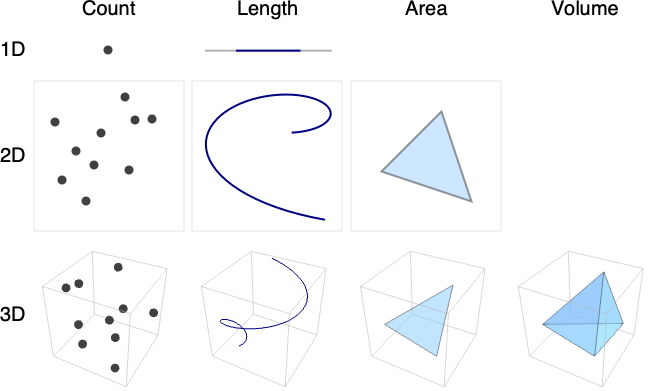
  • RegionMeasureは，数(0D)，長さ(1D)，面積(2D)，体積(3D)，ルベーグ(Lebesgue)測度としても知られている．
  • 行が埋込み次元，列が幾何学次元に相当する例
  • 領域 reg の次元が d≥0のときは，d 次元測度が使われる．
  • 零次元測度は，領域内の点の数を数える．
  • RegionMeasure[x,{{t1,a1,b1},…,{tk,ak,bk}}]では，x がスカラーならRegionMeasureは k+1次元の超曲面{t1,…,tk,x}の測度を返す．
  • RegionMeasureの第3引数における座標チャートはCoordinateChartDataの第1引数におけるのと同じ方法で3つトリプル{coordsys,metric,dim}を使って指定することができる．dim を省略した短縮形も使うことができる．
  • 次のオプションが使える．
  • AccuracyGoalInfinity目標絶対確度の桁数
    Assumptions $Assumptionsパラメータに関する仮定
    GenerateConditionsAutomaticパラメータについての条件を生成するかどうか
    PerformanceGoal$PerformanceGoalパフォーマンスのどの面について最適化するか
    PrecisionGoalAutomatic目標精度の桁数
    WorkingPrecision Automatic内部計算に使用する精度
  • 積分の記号極限は実数で順序付けられていると仮定される．記号座標チャートのパラメータはCoordinateChartDataの"ParameterRangeAssumptions"特性で与えられる範囲内の収まるものと仮定される．
  • RegionMeasureは，GeometricSceneの記号領域と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (6)

RegionMeasureは，零次元領域の点の数に相当する：

RegionMeasureは，一次元領域の曲線の長さに相当する：

RegionMeasureは，二次元領域の表面積に相当する：

RegionMeasureは，三次元領域の体積に相当する：

蝶ネクタイの形の面積：

円筒座標で表現された円筒の体積：

スコープ  (27)

特別な領域  (10)

Pointについての測度は数に相当する：

点は任意の次元で使うことができる：

Lineについての測度は弧長に相当する：

線は任意の次元で使うことができる：

Rectangleは2Dで使うことができ，この測度は面積に相当する：

Cuboidは任意の次元で使うことができる：

Simplexは，二次元では，点，線，三角形に相当し得る：

単体は任意の次元で使うことができる：

次元における標準的な単位単体の測度：

Polygonは面積を表す：

3Dで：

Diskは2Dで使うことができる：

Ballは任意の次元で使うことができる．測度は一般化された体積である：

次元における単位球体の測度：

楕円としてのDiskは2Dで使うことができる：

Ellipsoidは任意の次元で使うことができる：

Circleは2Dで使うことができる：

Cylinderは3Dで使うことができる：

Coneは3Dで使うことができる：

数式定義領域  (2)

ImplicitRegionとして表された円板の測度：

円柱の体積：

ParametricRegionとして表された円板の測度：

円板の有理パラメータ化を使う：

円柱の体積：

メッシュ領域  (2)

2DにおけるMeshRegionの測度：

3Dにおける：

BoundaryMeshRegionの測度：

3Dにおける：

派生領域  (3)

RegionIntersectionの測度：

TransformedRegionの測度：

RegionBoundaryの測度：

地理的領域  (2)

地理実体の多角形の測度：

GeoPositionを使った多角形：

GeoGridPositionを使った多角形の測度：

パラメトリック式  (8)

円弧の長さ：

極座標における有限長の無限曲線：

長半径5，短半径2のトーラスの表面積：

その内側の体積：

四次元空間に埋め込まれた「平らなトーラス」の面積：

五次元に埋め込まれた四次元球の超体積：

単位超立方体上の放物面関数グラフ の超体積：

単位球上の極間を「揺れる」曲線の長さ：

球の上のステレオ座標上の単位正方形の面積：

オプション  (4)

Assumptions  (2)

陰的領域は楕円と双曲線の両方を表すことができる：

仮定 を加えると楕円の長さのみが与えられる：

長半径が と である楕円の面積：

長半径は正であるという仮定を加えると答が簡単になる：

WorkingPrecision  (2)

機械演算を使って弧長を計算する：

30桁精度で面積を求める：

アプリケーション  (13)

点  (2)

点集合について計数測度が使われる．各点が1に数えられる：

一定した点の質量 について，測定値に を掛けて全体の質量を求める：

一定しない点の質量関数 についてはIntegrateを使う：

曲線  (4)

関数曲線の長さ：

陰的曲線の長さ：

3Dで：

ペアノ(Peano)曲線の長さについての式を求める：

一定した電荷密度 があるワイヤーに沿った総電荷を求める：

一定しない密度 の場合はIntegrateを使う：

曲面  (2)

関数曲面の面積：

矩形領域の全質量：

一様の質量密度 の場合：

で与えられる一定しない質量密度の場合はIntegrateを使う：

立体  (3)

一定した密度 のBallの全質量：

一定していない密度関数 にはIntegrateを使う：

Cone中のエタノールの質量を求める：

エタノールの密度：

円錐の体積：

円錐中のエタノールの質量：

Cylinderの質量を求める．ただし，質量の密度は一様ではなく で定義される：

円柱の密度：

円柱の体積：

円柱の質量：

高次元領域  (2)

次元単位球体の領域測度についての式を導出する：

3D超曲面の体積：

特性と関係  (10)

領域 ℛ についてのRegionMeasureは積分 で与えられる：

ArcLengthは一次元領域についてのRegionMeasureの特殊ケースである：

Areaは，二次元領域についてのRegionMeasureの特殊ケースである：

Volumeは，三次元領域についてのRegionMeasureの特殊ケースである：

使われる測度は，零次元の数を含むRegionDimensionによって決められる：

一次元についての長さ：

二次元についての面積：

三次元についての体積：

混合次元の領域については，RegionDimensionは最大の次元を与える：

次元は1なので，これは長さを計算する：

RegionMeasure[x,{t},c]はArcLength[x,t,c]に等しい：

RegionMeasure[x,{s,t},c]はArea[x,s,t,c]に等しい：

RegionMeasure[x,{s,t,u},c]はVolume[x,s,t,u,c]に等しい：

RegionCentroidは m=RegionMeasure[ℛ]のIntegrate[p,p∈ℛ]/m に等しい：

考えられる問題  (3)

RegionMeasureは，離散点については計数測度を使う：

次は，二次元ルベーグ測度を使うように指定する：

パラメトリック形式はパラメータ化を基本的なものとし，複数の被覆を数える：

パラメトリック形式の領域バージョンは画像の測度を計算する：

RegionMeasureは，厳密値による答が計算できないときは機械精度の演算を行う：

おもしろい例題  (1)

カントール(Cantor)集合の測度を求める：

最初の6回の反復の測度を計算する：

反復kの長さを求める：

極限における測度：

Wolfram Research (2014), RegionMeasure, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionMeasure.html （2019年に更新）.

テキスト

Wolfram Research (2014), RegionMeasure, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionMeasure.html （2019年に更新）.

CMS

Wolfram Language. 2014. "RegionMeasure." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/RegionMeasure.html.

APA

Wolfram Language. (2014). RegionMeasure. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionMeasure.html

BibTeX

@misc{reference.wolfram_2024_regionmeasure, author="Wolfram Research", title="{RegionMeasure}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/RegionMeasure.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionmeasure, organization={Wolfram Research}, title={RegionMeasure}, year={2019}, url={https://reference.wolfram.com/language/ref/RegionMeasure.html}, note=[Accessed: 21-November-2024 ]}