UniformDistribution
UniformDistribution
UniformDistribution[{min,max}]
min から max までの値を与える連続一様統計分布を表す．
0から1までの値を与える一様分布を表す．
UniformDistribution[{{xmin,xmax},{ymin,ymax},…}]
{{xmin,xmax},{ymin,ymax},…}の範囲上の多変量一様分布を表す．
標準的な n 次元単位超立方体上の多変量一様分布を表す．
詳細
- UniformDistributionは矩形分布としても知られている．
- 一様分布における値 x の確率密度は min≤x≤max では一定で，x<min または x>max では0である． »
- UniformDistributionでは，min と max は min<max である任意の実数でよい．
- UniformDistributionでは，min と max は単位次元が等しい任意の数量でよい． »
- UniformDistributionは，Mean，CDF，RandomVariate等の関数で使うことができる． »
予備知識
- UniformDistribution[{a,b}]は，区間
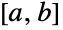内で確率変量が任意の値を取る確率が同程度である統計分布（矩形分布と呼ばれることもある）を表す．したがって，一様分布はその領域の端点によって完全にパラメータ化され，その確率密度関数は区間 
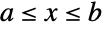で一定である．UniformDistribution[]を使って返されることがある標準一様分布は，区間
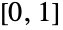にあるとみなされる．一様分布は，複数の変量にも一般化される．それぞれの変量は，同程度の確率で何らかの領域上にある． - ターゲットの確率変数の累積分布関数の逆関数を一様分布から選ばれた変量に適用することで，任意の分布からのサンプリングが可能な逆変換メソッドは，この分布の重要な応用である．他の重要な特性に，検定統計として連続分布で p 値を使った帰無仮説の検定の際に，帰無仮説が真である場合は p 値が標準一様分布に従うというものがある．
- RandomVariateを使って，1つまたは複数の機械精度あるいは任意精度（後者にはWorkingPrecisionオプションを使う）の擬似乱数変量を一様分布から与えることができる．Distributed[x,UniformDistribution[{a,b}]]は，より短縮した xUniformDistribution[{a,b}]と書くこともできるが，確率変数 x が一様分布に従って分布されていることを断言するために使うことができる．このよう断言は，Probability，NProbability，Expectation，NExpectation等の関数に使うことができる．
- 確率密度関数と累積分布関数はPDF[UniformDistribution[{a,b}],x]およびCDF[UniformDistribution[{a,b}],x]で与えられる．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って求めることができる．
- DistributionFitTestを使って与えられたデータ集合が一様分布と一致するかどうかをテストすることが，EstimatedDistributionを使って与えられたデータから一様パラメトリック分布を推定することが，FindDistributionParametersを使って一様分布にデータをフィットすることができる．ProbabilityPlotを使って，記号一様分布の累積分布関数に対するデータの累積分布関数のプロットを生成することができ，QuantilePlotを使って記号一様分布の変位値に対する指定されたデータの変位値プロットを生成することができる．
- TransformedDistributionを使って変換された一様分布を，CensoredDistributionを使って上限値と下限値の間で打ち切られた値の分布を，TruncatedDistributionを使って上下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使って，一様分布を含むより高次元の分布を構築することができ，ProductDistributionを使って一様分布を含む独立成分分布がある結合分布を計算することができる．
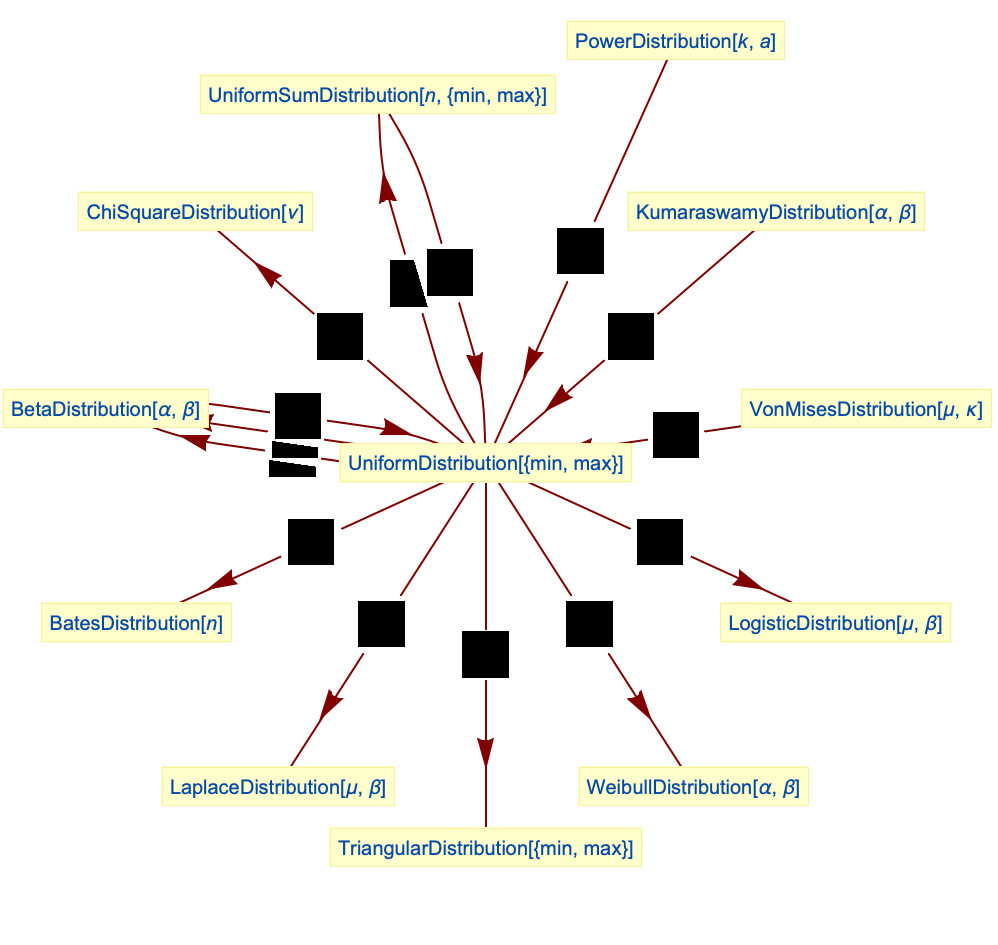
- 一様分布は他の多くの分布に関連している．例えば，UniformDistribution[]は，端点
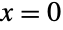および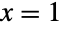 
においてモジュロを含むという意味でBetaDistributionおよびPowerDistributionの特殊ケースであり，PDF[UniformDistribution[],x]はPDF[BetaDistribution[1,1],x]とPDF[PowerDistribution[1,1],x]の両方と等しい．離散一様分布はDiscreteUniformDistributionで与えられ，UniformSumDistributionは一様分布を 
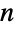個の一様確率変量の総和の分布に一般化する．2つの独立で同じように分布している一様分布の和は対称TriangularDistributionを与える．
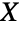が標準一様分布に従っているのであれば，
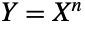はパラメータが
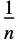と1のBetaDistributionに従う．標準一様分布（OrderDistribution[{UniformDistribution[],n},k]を使って求めることができる）からの，独立同分布に従うサンプル 
の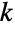 
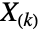の確率分布は，BetaDistribution[k,1-k+n]で与えられる．
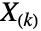の対応する期待値 （Expectation[x,xBetaDistribution[k,1-k+n]]で計算することができる） は
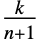で与えられる．他の緊密に関連する分布には，VonMisesDistribution，LogisticDistribution，WeibullDistribution，LaplaceDistribution，BatesDistribution，ChiSquareDistributionがある．
例題
すべて開く すべて閉じる例 (4)
Plot[Table[PDF[UniformDistribution[{0, max}], x], {max, {1, 2, 4}}]//Evaluate, {x, 0, 5}, PlotRange -> All, Filling -> Axis]PDF[UniformDistribution[{min, max}], x]Plot[Table[CDF[UniformDistribution[{0, max}], x], {max, {1, 2, 4}}]//Evaluate, {x, 0, 5}, Filling -> Axis, Exclusions -> None]CDF[UniformDistribution[{min, max}], x]Mean[UniformDistribution[{min, max}]]Variance[UniformDistribution[{min, max}]]Median[UniformDistribution[{min, max}]]スコープ (15)
Table[Plot3D[PDF[UniformDistribution[{{1, 3}, {1, d}}], {x, y}], {x, 0, 4}, {y, 0, d + 1}, AxesLabel -> Automatic, PlotLabel -> Row[{"d = ", d}]], {d, {3, 5}}]PDF[UniformDistribution[{{a, b}, {c, d}}], {x, y}]Table[Plot3D[CDF[UniformDistribution[{{1, 3}, {1, d}}], {x, y}], {x, 0, 4}, {y, 0, d + 1}, Exclusions -> None, AxesLabel -> Automatic, PlotLabel -> Row[{"d = ", d}]], {d, {3, 5}}]CDF[UniformDistribution[{{a, b}, {c, d}}], {x, y}]Mean[UniformDistribution[{{a, b}, {c, d}}]]Variance[UniformDistribution[{{a, b}, {c, d}}]]Covariance[UniformDistribution[{{a, b}, {c, d}}]]//MatrixFormdata = RandomVariate[UniformDistribution[{1, 3}], 10 ^ 4];Show[
Histogram[data, 20, "PDF"],
Plot[PDF[UniformDistribution[{1, 3}], x], {x, 0, 3}, PlotStyle -> Thick]]sample = RandomVariate[UniformDistribution[{1, 4}], 10 ^ 3];edist = EstimatedDistribution[sample, UniformDistribution[{min, max}]]サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：
Show[Histogram[sample, Automatic, "PDF"], Plot[PDF[edist, x], {x, 1, 4}, PlotStyle -> Thick]]sample = RandomVariate[UniformDistribution[{{0, 3}, {1, 4}}], 10 ^ 3];edist = EstimatedDistribution[sample, UniformDistribution[{{a, b}, {c, d}}]]Skewness[UniformDistribution[{min, max}]]Skewness[UniformDistribution[{{a, b}, {c, d}, {e, f}}]]Kurtosis[UniformDistribution[{min, max}]]Kurtosis[UniformDistribution[{{a, b}, {c, d}, {e, f}}]]Correlation[UniformDistribution[{{a, b}, {c, d}, {e, f}}]]//MatrixFormFormulaGrid[list_, type_] := Grid[...]FormulaGrid[Table[Moment[UniformDistribution[{min, max}], k], {k, 5}], M]Moment[UniformDistribution[{min, max}], r]FormulaGrid[Table[CentralMoment[UniformDistribution[{min, max}], k], {k, 5}], CM]CentralMoment[UniformDistribution[{min, max}], r]FormulaGrid[Table[FactorialMoment[UniformDistribution[{min, max}], k], {k, 5}], FM]FormulaGrid[Table[Cumulant[UniformDistribution[{min, max}], k], {k, 5}], C]Cumulant[UniformDistribution[{min, max}], r]FormulaGrid[list_, type_] := Grid[...]FormulaGrid[Table[Moment[UniformDistribution[{{a, b}, {c, d}}], {2, k}]//Simplify, {k, 1, 3}], M]Moment[UniformDistribution[{{a, b}, {c, d}}], {r, k}]FormulaGrid[Table[CentralMoment[UniformDistribution[{{a, b}, {c, d}}], {2, k}]//FullSimplify, {k, 1, 3}], CM]CentralMoment[UniformDistribution[{{a, b}, {c, d}}], {r, k}]FormulaGrid[Table[FactorialMoment[UniformDistribution[{{a, b}, {c, d}}], {2, k}]//Simplify, {k, 1, 3}], FM]FormulaGrid[Table[Cumulant[UniformDistribution[{{a, b}, {c, d}}], {2, k}]//Simplify, {k, 0, 3}], C]Cumulant[UniformDistribution[{{a, b}, {c, d}}], {r, k}]Plot[Table[HazardFunction[UniformDistribution[{0, max}], x], {max, {1, 3, 4}}]//Evaluate, {x, 0, 4}, Filling -> Axis]HazardFunction[UniformDistribution[{min, max}], x]Table[Plot3D[HazardFunction[UniformDistribution[{{1, 3}, {1, d}}], {x, y}], {x, 1, 3}, {y, 1, d}, AxesLabel -> Automatic, PlotLabel -> Row[{"d = ", d}]], {d, {3, 5}}]HazardFunction[UniformDistribution[{{a, b}, {c, d}}], {x, y}]Plot[Table[Quantile[UniformDistribution[{0, max}], q], {max, {1, 3, 5}}]//Evaluate, {q, 0, 1}, Filling -> Axis]Quantile[UniformDistribution[{min, max}], q]𝒟 = UniformDistribution[{{a, b}, {c, d}, {e, f}}];MarginalDistribution[𝒟, 1]MarginalDistribution[𝒟, {2, 3}]母数でQuantityを一貫して使うとQuantityDistributionが与えられる：
sideLength𝒟 = UniformDistribution[{Quantity[1, "Meters"], Quantity[3, "Meters"]}]Mean[TransformedDistribution[w h, {wsideLength𝒟, hsideLength𝒟}]]Quantity母数は各次元内でのみ一貫していなければならない：
heightWeight𝒟 = UniformDistribution[{{Quantity[160, "Centimeters"], Quantity[190, "Centimeters"]}, {Quantity[70, "Kilograms"], Quantity[120, "Kilograms"]}}]Mean[heightWeight𝒟]アプリケーション (12)
Probability[x < Mean[UniformDistribution[{min, max}]], xUniformDistribution[{min, max}]]//Simplify無作為に選んだ円周上の2つの点が 
より小さい角を成す確率を求める：
Probability[Abs[Mod[Subscript[θ, 1] - Subscript[θ, 2], 2Pi]] < Pi / 4, {Subscript[θ, 1]UniformDistribution[{0, 2π}], Subscript[θ, 2]UniformDistribution[{0, 2π}]}]Graphics[Point[Table[{Cos[θ], Sin[θ]}, {θ, RandomVariate[UniformDistribution[{0, 2π}], 100]}]]]invcdf[q_] = InverseCDF[ExtremeValueDistribution[2, 3], q]data = invcdf /@ RandomVariate[UniformDistribution[{0, 1}], 10 ^ 4];Show[Histogram[data, 20, "PDF"], Plot[PDF[ExtremeValueDistribution[2, 3], x], {x, -5, 30}, PlotStyle -> Thick]]速さ 
，角度 
（等しい確率で 
から 
まで変化）で水を噴き出す噴水のノズルがある．水が地面に達する地点までの予期される水平距離を求める：
Expectation[v ^ 2 2 Sin[α]Cos[α] / g, α UniformDistribution[{π / 6, π / 3}]]ランダムな長方形の辺の長さは10mから0メートルの間で一様分布に従っている：
len𝒟 = UniformDistribution[{Quantity[10, "Meters"], Quantity[20, "Meters"]}]Mean[TransformedDistribution[w h, {wlen𝒟, hlen𝒟}]]Mean[TransformedDistribution[w ^ 2, wlen𝒟]]//N正弦波信号の位相角 
は
から
までで一様分布に従っている．
が 
から 
までの間になる確率を求める：
𝒟 = UniformDistribution[{0, 2π}];Probability[π / 4 ≤ θ ≤ π / 2, θ𝒟]
Probability[θ ≤ π / 3, θ𝒟]
Mean[𝒟]
sd = StandardDeviation[𝒟]Probability[Mean[𝒟] - sd ≤ θ ≤ Mean[𝒟] + sd, θ𝒟]2台の列車が別々に駅に着き，それぞれ10分間停車する．到着時刻が一様分布に従うものとして，2台の列車が1時間以内に駅で出会う確率を求める：
trains𝒟 = UniformDistribution[{Quantity[{0, 60}, "Minutes"], Quantity[{0, 60}, "Minutes"]}]Probability[Abs[x - y] < Quantity[10, "Minutes"], {x, y}trains𝒟]RegionPlot[Abs[x - y] < 10, {x, 0, 60}, {y, 0, 60}, FrameLabel -> {"train 1", "train 2"}]直径 
の一様分布に従う軸と，内径 
の一様分布に従う軸管とが互いに無関係に生産されている．2つの直径の最適な差を
までとして，軸が軸管にフィットする確率を求める：
NProbability[dh - Quantity[0.5, "Millimeters"] < ds < dh, dsUniformDistribution[{Quantity[48.5, "Millimeters"], Quantity[50.5, "Millimeters"]}] && dhUniformDistribution[{Quantity[49, "Millimeters"], Quantity[51, "Millimeters"]}]]RegionPlot[{x^2 + y^2 < (50.5 / 2)^2, (49 / 2)^2 < x^2 + y^2}, {x, 0, 50.5 / 2}, {y, 0, 50.5 / 2}, PlotPoints -> 50]あるデバイスの寿命が一様分布に従っている．そのデバイスの信頼性を求める：
sf = SurvivalFunction[UniformDistribution[{0, max}], t]HazardFunction[UniformDistribution[{0, max}], t]rs = SurvivalFunction[UniformDistribution[{0, max1}], t]SurvivalFunction[UniformDistribution[{0, max2}], t]//PiecewiseExpandrp = 1 - (1 - SurvivalFunction[UniformDistribution[{0, max1}], t])(1 - SurvivalFunction[UniformDistribution[{0, max2}], t])//PiecewiseExpand両方の系の信頼性を max1=10，max2=15について求める：
Block[{max1 = 10, max2 = 15}, Plot[{rs, rp}, {t, 0, 15}, PlotLegends -> {"in series", "in parallel"}]]CompareHistogram3D[dist_, {xmin_, xmax_, dx_}, {ymin_, ymax_, dy_}, df_ : PDF, opts___ ? OptionQ] :=
Module[{hist, dplot},
hist = Histogram3D[RandomVariate[dist, 10 ^ 4], {{xmin, xmax, dx}, {ymin, ymax, dy}}, ToString[df], PlotRange -> {{xmin, xmax}, {ymin, ymax}, All}, ChartBaseStyle -> Opacity[0.5]];
dplot = Plot3D[df[dist, {x, y}], {x, xmin, xmax}, {y, ymin, ymax}, Mesh -> {Range[xmin, xmax, dx], Range[ymin, ymax, dy]}, PlotRange -> All, MeshStyle -> Gray, PlotStyle -> Hue[.15, .7, .8]];
Show[hist, dplot]
];𝒟 = UniformDistribution[{{ 2, 4}, {1, 3}}];CompareHistogram3D[𝒟, {1, 5, .5}, {0, 4, .5}, PDF]CompareHistogram3D[𝒟, {1, 5, .5}, {0, 4, .5}, CDF]
𝒫 = WhiteNoiseProcess[UniformDistribution[{-1, 1}]];data = RandomFunction[𝒫, {0, 70}];ListPlot[data, Filling -> Axis]特性と関係 (21)
TransformedDistribution[a * u + b, uUniformDistribution[{min, max}], Assumptions -> a > 0]TransformedDistribution[-3.4 u + b, uUniformDistribution[{min, max}]]TruncatedDistribution[{a, b}, UniformDistribution[{min, max}]]
個の一様確率変数の和はUniformSumDistributionに従う：
CharacteristicFunction[UniformDistribution[{min, max}], t] ^ nCharacteristicFunction[UniformSumDistribution[n, {min, max}], t]% - %%TransformedDistribution[(u + v + w), {u, v, w}ProductDistribution[{UniformDistribution[{0, 1}], 3}]]
個の一様変数の平均はBatesDistributionに従う：
(CharacteristicFunction[UniformDistribution[{0, 1}], t / n]) ^ nCharacteristicFunction[BatesDistribution[n], t]% - %%𝒟 = TransformedDistribution[(u + v + w) / 3, {u, v, w}UniformDistribution[3]];PDF[𝒟, x]PDF[BatesDistribution[3], x]FullSimplify[% - %%]DiscreteUniformDistributionはUniformDistributionの離散型の類似物である：
PDF[UniformDistribution[{min, max}], x]PDF[DiscreteUniformDistribution[{min, max}], x]2つの一様確率変数の平均はTriangularDistributionに従う：
𝒟 = Assuming[{a > 0}, TransformedDistribution[(u + v) / 2, {u, v}ProductDistribution[{UniformDistribution[{0, a}], 2}]]];Block[{a = 2}, Show[Histogram[RandomVariate[𝒟, 10 ^ 4], 20, "PDF"], Plot[PDF[TriangularDistribution[{0, a}], x], {x, 0, a}, PlotStyle -> Thick]]]PDF[𝒟, x]//FullSimplify[#, a > 0]&PDF[TriangularDistribution[{0, a}], x]FullSimplify[% - %%, a > 0 && 0 < x < a]CharacteristicFunction[UniformDistribution[{min, max}], t / 2] ^ 2CharacteristicFunction[TriangularDistribution[{min, max}], t]%% - %//FullSimplifyExponentialDistributionは 
が一様分布に従う 
の極限分布である：
mindist = OrderDistribution[{UniformDistribution[{0, 1}], n}, 1];CDF[mindist, x / n]Limit[CDF[mindist, x / n], n -> ∞]CDF[ExponentialDistribution[1], x]% - %%//FullSimplifyBetaDistributionは一様分布に従う変数の順序分布である：
OrderDistribution[{UniformDistribution[{0, 1}], n}, k]BetaDistributionはUniformDistributionを変換したものである：
TransformedDistribution[u ^ a, uUniformDistribution[]]ArcSinDistributionはUniformDistributionを変換したものである：
TransformedDistribution[Sin[x], xUniformDistribution[{-π, π}]]TransformedDistribution[Cos[x], xUniformDistribution[{-π, π}]]UniformDistributionはBetaDistributionを変換したものである：
TransformedDistribution[u ^ a, uBetaDistribution[a, 1]]UniformDistributionはKumaraswamyDistributionを変換したものである：
TransformedDistribution[u ^ a, uKumaraswamyDistribution[a, 1]]UniformDistributionはPowerDistributionを変換したものである：
TransformedDistribution[u ^ a, uPowerDistribution[1, a]]ChiSquareDistributionはUniformDistributionを変換したものである：
𝒟 = TransformedDistribution[-2 Log[u], uUniformDistribution[{0, 1}]];PDF[𝒟, x]//FullSimplify[#, x∈Reals]&PDF[ChiSquareDistribution[2], x]FullSimplify[% - %%, x > 0]LaplaceDistributionはUniformDistributionを変換したものである：
TransformedDistribution[Log[u / v], {u, v}ProductDistribution[{UniformDistribution[{0, a}], 2}], Assumptions -> a > 0]LogisticDistributionはUniformDistributionを変換したものである：
𝒟 = TransformedDistribution[μ + β(Log[u] - Log[1 - u]), uUniformDistribution[{0, 1}]] ;PDF[𝒟, x]//Simplify[#, β > 0]&PDF[LogisticDistribution[μ, β], x]Simplify[% - %%]UniformDistributionはVonMisesDistributionの特殊ケースである：
PDF[VonMisesDistribution[μ, 0], x]PDF[UniformDistribution[{μ - π, μ + π}], x]% - %%//SimplifyWeibullDistributionはUniformDistributionを変換したものである：
𝒟 = TransformedDistribution[β (-Log[1 - u]) ^ (1 / α), uUniformDistribution[{0, 1}]];Block[{α = 3, β = 0.6}, Show[Histogram[RandomVariate[𝒟, 10 ^ 4], 20, "PDF"], Plot[PDF[WeibullDistribution[α, β], x], {x, 0, 1.5}, PlotStyle -> Thick]]]WaringYuleDistributionはGeometricDistributionとUniformDistributionの母数混合分布である：
𝒟 = ParameterMixtureDistribution[GeometricDistribution[w^1 / a], wUniformDistribution[], Assumptions -> a > 0];PDF[𝒟, x]PDF[WaringYuleDistribution[a], x]FullSimplify[% - %%]PDF[CopulaDistribution["Product", {UniformDistribution[{a, b}], UniformDistribution[{c, d}]} ], {x, y}]PDF[UniformDistribution[{{a, b}, {c, d}}], {x, y}]% - %%//FullSimplify[#, a < x < b && c < y < d]&考えられる問題 (2)
UniformDistributionは，min あるいは max が実数ではないときは定義されない：
Mean[UniformDistribution[{3 + I, 4}]]
UniformDistributionは， min ≥ max のときは定義されない：
Mean[UniformDistribution[{8, 6}]]
Mean[UniformDistribution[{min, max}]] /. {min -> 3 + I}おもしろい例題 (1)
累積分布関数の等高線を持つ max のさまざまな値についての確率密度関数：
cdf = Function[{x, max}, Evaluate[CDF[UniformDistribution[{0, max}], x]]];
ql = {0.025, 0.10, 0.25, 0.5, 0.75, 0.90, 0.975};
cl = Table[ColorData["Rainbow"][q], {q, Join[{0.0}, ql]}];Legended[Plot3D[PDF[UniformDistribution[{0, max}], x], {x, -2, 6}, {max, 1, 5}, PlotTheme -> "Marketing", MeshFunctions -> {cdf}, Mesh -> {ql}, MeshStyle -> GrayLevel[0.8], MeshShading -> cl, AxesLabel -> Automatic, PlotPoints -> 100, BaseStyle -> Opacity[0.9], ImageSize -> 400, PlotRange -> All, Exclusions -> None], BarLegend["Rainbow", ql, LegendLabel -> "prob"]]
Wolfram Research (2007), UniformDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/UniformDistribution.html （2016年に更新）.
テキスト
Wolfram Research (2007), UniformDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/UniformDistribution.html （2016年に更新）.
CMS
Wolfram Language. 2007. "UniformDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/UniformDistribution.html.
APA
Wolfram Language. (2007). UniformDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UniformDistribution.html