UniformSumDistribution
0から1まで一様に分布した n 個の確率変数の和の分布を表す.
UniformSumDistribution[n,{min,max}]
min から max まで一様に分布した n 個の確率変数の和の分布を表す.
詳細

- UniformSumDistributionはIrwin–Hall分布としても知られている.
- 一様確率変数の和の分布における値
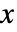 の確率密度は,
の確率密度は,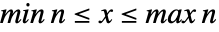 では
では 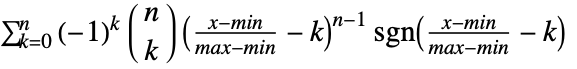 に比例し,それ以外ではゼロである.
に比例し,それ以外ではゼロである. - UniformSumDistribution[n,{min,max}]は各 xi がUniformDistribution[{min,max}]からのものであるTransformedDistribution[x1+⋯+xn,…]に等しい.
- UniformSumDistributionでは,n は任意の正の整数でよく,min と max は min<max である任意の実数でよい.
- UniformSumDistributionでは,min と max は単位次元が等しい任意の数量でよく,n は無次元量でよい. »
- UniformSumDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- UniformSumDistribution[n,{min,max}]は,min から max までの区間で定義され,正の整数 n でパラメータ化された統計分布を表す.一様確率変数の和の分布の確率密度関数(PDF)の全体的な形は,n によって著しく変わり,
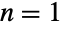 では一様,
では一様,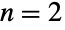 では三角,
では三角,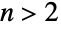 では最大値が
では最大値が 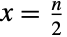 の単峰となる.1引数の形のUniformSumDistribution[n]はUniformSumDistribution[n,{0,1}]に等しく,標準化された一様確率変数の和の分布と呼ばれることがある.一様確率変数の和の分布はIrwin–Hall 分布としても知られている.
の単峰となる.1引数の形のUniformSumDistribution[n]はUniformSumDistribution[n,{0,1}]に等しく,標準化された一様確率変数の和の分布と呼ばれることがある.一様確率変数の和の分布はIrwin–Hall 分布としても知られている. - 一様確率変数の和の分布UniformSumDistribution[n]は,統計的に独立な一様分布に従う n 個の確率変数
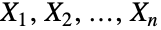 の和として定義される.つまり,XUniformSumDistribution[n]は
の和として定義される.つまり,XUniformSumDistribution[n]は 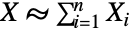 であると言うのに等しい.ただし,すべての
であると言うのに等しい.ただし,すべての 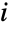 について XiUniformDistribution[]である.2引数の形のUniformSumDistribution[n,{min,max}]も,XiUniformDistribution[{min,max}]という例外を除いて同じ意味を持つ.一様確率変数の和の分布の重要な応用の1つは計算にある.歴史的に,
について XiUniformDistribution[]である.2引数の形のUniformSumDistribution[n,{min,max}]も,XiUniformDistribution[{min,max}]という例外を除いて同じ意味を持つ.一様確率変数の和の分布の重要な応用の1つは計算にある.歴史的に,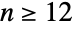 の標準化された一様確率変数の和の分布が標準正規変数の生成に使われてきた.この事実にもかかわらず,UniformSumDistribution[n]が(NormalDistributionとは違って)完全に平坦ではない点は注目に値する.これは,UniformSumDistributionのPDFが
の標準化された一様確率変数の和の分布が標準正規変数の生成に使われてきた.この事実にもかかわらず,UniformSumDistribution[n]が(NormalDistributionとは違って)完全に平坦ではない点は注目に値する.これは,UniformSumDistributionのPDFが 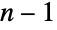 の導関数を取った後では平坦ではなくなるのからである.UniformSumDistributionは多くの工学分野での応用にも見られ,特にさまざまな工業製品の寿命のモデル化に特に役に立つ.
の導関数を取った後では平坦ではなくなるのからである.UniformSumDistributionは多くの工学分野での応用にも見られ,特にさまざまな工業製品の寿命のモデル化に特に役に立つ. - RandomVariateを使って一様確率変数の和の分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,UniformSumDistribution[n,{min,max}]](より簡略すると xUniformSumDistribution[n,{min,max}])を使って,確率変数 x が一様確率変数の和の分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[UniformSumDistribution[n,{min,max}],x]およびCDF[UniformSumDistribution[n,{min,max}],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が一様確率変数の和の分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから一様確率変数の和のパラメトリック分布を推定することが,FindDistributionParametersを使ってデータを一様確率変数の和の分布にフィットすることができる.ProbabilityPlotを使って一様確率変数の和の分布の記号分布CDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って一様確率変数の和の分布の記号分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された一様確率変数の和の分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って一様確率変数の和の分布を含む高次元分布を構築することが,ProductDistributionを使って一様確率変数の和の分布を含む独立成分分布の結合分布を計算することができる.
- UniformSumDistributionは他の数多くの分布と関連している.例えば,一様確率変数の和の分布のPDFは,
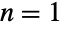 のときは厳密にUniformDistributionであり,
のときは厳密にUniformDistributionであり,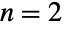 のときは厳密にTriangularDistributionである.また,大きい
のときは厳密にTriangularDistributionである.また,大きい 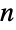 の値については,視覚的にNormalDistributionのPDFに似て見える.(この類似性は,UniformSumDistribution[n]が NormalDistribution[μ,σ]に近付くことによる.μ および σ は,それぞれUniformSumDistribution[n]の平均と標準偏差を表す).UniformSumDistributionはまた,統計的に独立の一様分布に従う確率変数の(和ではなく)平均を表すBatesDistributionと密接な関係がある.
の値については,視覚的にNormalDistributionのPDFに似て見える.(この類似性は,UniformSumDistribution[n]が NormalDistribution[μ,σ]に近付くことによる.μ および σ は,それぞれUniformSumDistribution[n]の平均と標準偏差を表す).UniformSumDistributionはまた,統計的に独立の一様分布に従う確率変数の(和ではなく)平均を表すBatesDistributionと密接な関係がある.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
KurtosisはNormalDistributionの尖度と同じであることが多い:
ハザード関数には閉形式はないが,数値的に計算することができる:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (3)
寿命が尽きるまでにA,B,Cの3段階あるデバイスがある.各段階の時間は![]() 上で一様分布に従う.段階Cが終るとデバイスは故障する.このデバイスの故障までの時間の分布を求める:
上で一様分布に従う.段階Cが終るとデバイスは故障する.このデバイスの故障までの時間の分布を求める:
このようなデバイスが最低でも20時間使用可能である確率を求める:
互いに独立のこのようなデバイス30個の故障までの時間のシミュレーションを行う:
累積分布関数もまたUniformSumDistributionから導くことができる:
特性と関係 (6)
UniformSumDistributionはスケーリングの下では閉じている:
スケーリング因子の符号あるいは数値についての仮定が必要である:
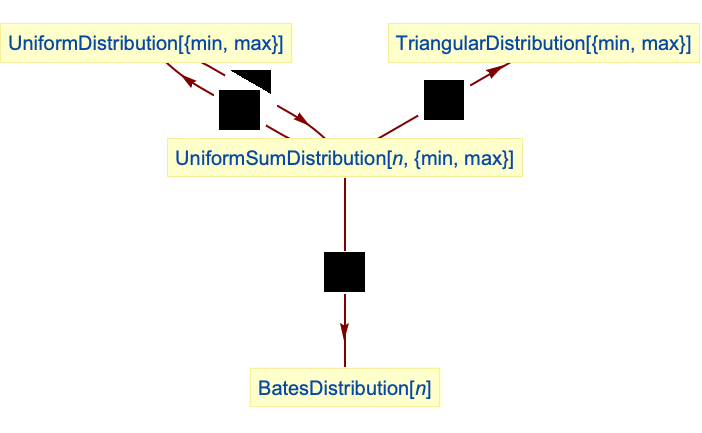
n 個の一様確率変数の和はUniformSumDistributionに従う:
n 個の一様変数の平均はBatesDistributionに従う:
2個の一様変数の平均はTriangularDistributionに従う:
UniformSumDistributionは中心極限定理を説明する:
テキスト
Wolfram Research (2010), UniformSumDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/UniformSumDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "UniformSumDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/UniformSumDistribution.html.
APA
Wolfram Language. (2010). UniformSumDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UniformSumDistribution.html