CompleteGraph

CompleteGraph[n]

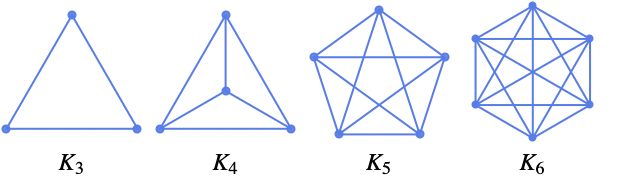
n 個の頂点を持つ完全グラフ を与える．

CompleteGraph[{n1,n2,…,nk}]

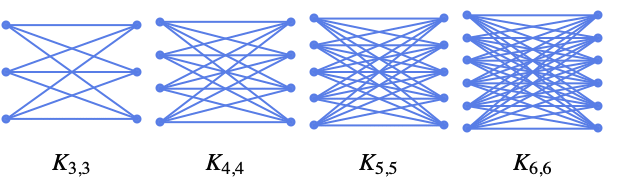
頂点数が n1+n2+⋯+nk の完全 k 部グラフ を与える．

詳細とオプション

例題

すべて開くすべて閉じる

例  (4)

最初のいくつかの完全グラフ ：

二部グラフ ：

有向完全グラフはそれぞれの無向辺に2つの有向辺を使う：

有向完全 部グラフは1つのグループから他のグループへ有向辺を使う：

オプション  (81)

AnnotationRules  (2)

頂点の注釈を指定する：

辺の注釈を指定する：

DirectedEdges  (2)

デフォルトで，無向グラフが生成される：

DirectedEdges->Trueを使って有向グラフを生成する：

有向 部グラフ：

EdgeLabels  (7)

辺12にラベルを付ける：

すべての辺に別々にラベルを付ける：

任意の式をラベルとして使う：

Placedを記号位置と一緒に使って辺に沿ったラベル位置を制御する：

ラベルを置くために明示的な座標を使う：

ラベル内で位置を変える：

複数のラベルを置く：

TooltipとStatusAreaの値から自動でラベル付けを行う：

EdgeShapeFunction  (6)

EdgeShapeFunctionの組込み設定のリストを得る：

基線を含む無向辺：

辺に異なるグリフの付いた線：

実線の矢印を含む有向辺：

線の矢印：

塗潰しのない矢印：

個別の辺に対して辺関数を指定する：

さまざまなデフォルトの辺関数と組み合せる：

プログラムを実行して辺を描画する：

EdgeShapeFunctionはEdgeStyleと組み合せることができる：

EdgeShapeFunctionはEdgeStyleより優先順位が高い：

EdgeStyle  (2)

すべての辺にスタイルを付ける：

個々の辺にスタイルを付ける：

EdgeWeight  (2)

すべての辺の重みを指定する：

任意の数式を重みとして使う：

GraphHighlight  (3)

頂点1をハイライトする：

辺23をハイライトする：

頂点と辺をハイライトする：

GraphHighlightStyle  (2)

GraphHighlightStyleの組込み設定のリストを得る：

GraphHighlightStyleの組込み設定を使う：

GraphLayout  (5)

デフォルトで，レイアウトは自動的に選ばれる：

特殊な曲線のレイアウトを指定する：

最適化の基準を満足するレイアウトを指定する：

VertexCoordinatesはGraphLayoutの座標を無効にする：

AbsoluteOptionsを使って，レイアウトアルゴリズムで計算されたVertexCoordinatesを抽出する：

PlotTheme  (4)

基本テーマ  (2)

一般的な基本テーマを使う：

白黒のテーマを使う：

特徴テーマ  (2)

大きいグラフのテーマを使う：

古典的な図表テーマを使う：

VertexCoordinates  (3)

デフォルトで，任意の頂点座標は自動的に計算される：

AbsoluteOptionsを使って結果の頂点座標を抽出する：

楕円に沿ったレイアウト関数を指定する：

これを使ってグラフの頂点座標を生成する：

VertexCoordinatesはGraphLayoutより優先順位が高い：

VertexLabels  (13)

頂点名をラベルとして使う：

個々の頂点にラベルを付ける：

すべての頂点にラベルを付ける：

任意の式をラベルとして使う：

Placedを記号位置と一緒に使って外側の位置を含むラベルの置き方を制御する：

記号的外側コーナーの位置：

記号的内側位置：

記号的内側コーナーの位置：

明示的な座標を使ってラベルの中央を位置付ける：

すべてのラベルを頂点の右上コーナーに置き，ラベル内の座標を変える：

複数のラベルを置く：

任意の数のラベルを使うことができる：

Placedの引数を使ってTooltipを含むフォーマットを制御する：

あるいはStatusAreaを含むフォーマットを制御する：

より高度のフォーマット関数を使う：

VertexShape  (5)

Graphics，Image，Graphics3Dの任意のものを頂点の形として使う：

個々の頂点の形を指定する：

VertexShapeはVertexSizeと組み合せることができる：

VertexShapeはVertexStyleの影響を受けない：

VertexShapeFunctionはVertexShapeよりも優先順位が高い：

VertexShapeFunction  (10)

組込みのVertexShapeFunctionコレクションのリストを得る：

"Basic"コレクションのVertexShapeFunctionの組込み設定を使う：

簡単な基本形：

一般的な基本形：

"Rounded"コレクションのVertexShapeFunctionの組込み設定を使う：

"Concave"コレクションのVertexShapeFunctionの組込み設定を使う：

個々の頂点を描画する：

デフォルトの頂点関数と組み合せる：

定義済みのグラフィックスを使って頂点を描画する：

プログラムを実行して頂点を描画する：

VertexShapeFunctionはVertexStyleと組み合せることができる：

VertexShapeFunctionはVertexStyleより優先順位が高い：

VertexShapeFunctionはVertexShapeと組み合せることができる：

VertexShapeFunctionはVertexShapeより優先順位が高い：

VertexSize  (8)

デフォルトで，頂点の大きさは自動的に計算される：

記号的な頂点サイズを使ってすべての頂点の大きさを指定する：

頂点座標間の最短距離との比を使う：

すべての頂点座標に全体的な対角との比を使う：

軸方向と 軸方向の両方に大きさを指定する：

個々の頂点の大きさを指定する：

VertexSizeはVertexShapeFunctionと組み合せることができる：

VertexSizeはVertexShapeと組み合せることができる：

VetexStyle  (5)

すべての頂点にスタイルを付ける：

個々の頂点にスタイルを付ける：

VertexShapeFunctionはVertexStyleと組み合せることができる：

VertexShapeFunctionはVertexStyleよりも優先順位が高い：

VertexStyleはBaseStyleと組み合せることができる：

VertexStyleはBaseStyleより優先順位が高い：

VertexShapeはVertexStyleの影響を受けない：

VertexWeight  (2)

すべての頂点について重みを設定する：

任意の数式を重みとして使う：

アプリケーション  (7)

完全グラフのGraphCenterにはすべての頂点が含まれる：

GraphPeripheryはすべての頂点を含む：

VertexEccentricityはすべての頂点について1である：

頂点離心経路をハイライトする：

GraphRadiusは1である：

半径経路をハイライトする：

GraphDiameterは1である：

直径経路をハイライトする：

から までの頂点連結性は から までの頂点独立経路の数である：

任意の頂点ペアの間に3つの頂点独立経路がある：

CompleteGraph[n]の頂点連結性は である：

CompleteGraphの頂点次数をハイライトする：

接近中心性をハイライトする：

固有ベクトル中心性をハイライトする：

特性と関係  (12)

CompleteGraph[n]の頂点の数：

CompleteGraph[n]の辺の数：

完全グラフは正則グラフである：

完全グラフの部分グラフは完全グラフである：

完全グラフの頂点の近傍はグラフ自身である：

完全グラフはそれ自身のクリークである：

辺のない完全グラフのGraphComplement：

完全グラフでは，AdjacencyMatrixの対角の外側のすべての項は1である：

完全 部グラフでは，対角ブロックの外側の項はすべて1である：

完全グラフ は巡回グラフ である：

完全グラフ は車輪グラフ である：

完全グラフ は星型グラフ の線グラフである：

おもしろい例題  (2)

完全グラフのランダムなコラージュ：

頂点が素数の完全グラフのサイクル分解に彩色する：

Wolfram Research (2010), CompleteGraph, Wolfram言語関数， https://reference.wolfram.com/language/ref/CompleteGraph.html （2020年に更新）.

テキスト

Wolfram Research (2010), CompleteGraph, Wolfram言語関数， https://reference.wolfram.com/language/ref/CompleteGraph.html （2020年に更新）.

CMS

Wolfram Language. 2010. "CompleteGraph." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/CompleteGraph.html.

APA

Wolfram Language. (2010). CompleteGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompleteGraph.html

BibTeX

@misc{reference.wolfram_2024_completegraph, author="Wolfram Research", title="{CompleteGraph}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CompleteGraph.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_completegraph, organization={Wolfram Research}, title={CompleteGraph}, year={2020}, url={https://reference.wolfram.com/language/ref/CompleteGraph.html}, note=[Accessed: 21-November-2024 ]}