ComplexContourPlot[f,{z,zmin,zmax}]
生成 f 作为 z 的函数的填充等值线图.
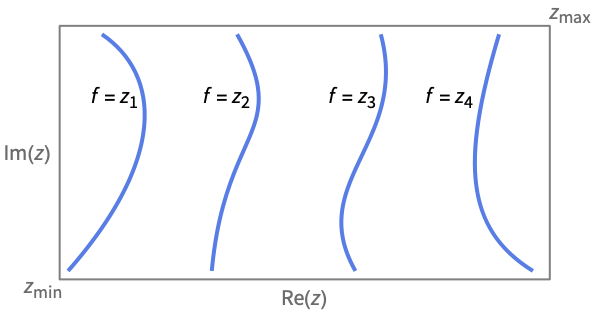
ComplexContourPlot[{f1,f2,…},{z,zmin,zmax}]
生成 f1、f2、… 的等值线.
ComplexContourPlot[f==g,{z,zmin,zmax}]
绘制 f=g 的等值线.
ComplexContourPlot[{f1==g1,f2==g2,…},{z,zmin,zmax}]
绘制 f1g1、f2=g2、… 的等值线.




ComplexContourPlot
ComplexContourPlot[f,{z,zmin,zmax}]
生成 f 作为 z 的函数的填充等值线图.
ComplexContourPlot[{f1,f2,…},{z,zmin,zmax}]
生成 f1、f2、… 的等值线.
ComplexContourPlot[f==g,{z,zmin,zmax}]
绘制 f=g 的等值线.
ComplexContourPlot[{f1==g1,f2==g2,…},{z,zmin,zmax}]
绘制 f1g1、f2=g2、… 的等值线.
更多信息和选项




- 在 f 值不为实数的位置,会留下孔,可看到等值线图的背景. 函数 f 和 g 通常会涉及如 Re、Im、Abs 和 Arg 等这样的函数,从复数中提取实部以进行比较.
- ComplexContourPlot[f,{z,n}] 等价于 ComplexContourPlot[f,{z,-n-n I,n+n I}].
- ComplexContourPlot 将变量 z 视为局部变量,相当于使用 Block.
- ComplexContourPlot 具有属性 HoldAll,在对 z 赋值后才计算 fi 和 gi. 某些情况下,先用 Evaluate 对 f 和 g 进行符号式计算效率更高.
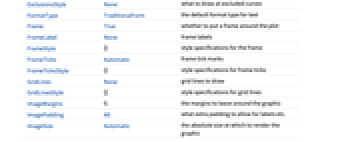
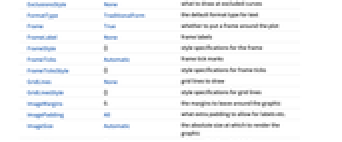
- ComplexContourPlot 和 Graphics 有相同的选项,不同之处和更多选项如下所示: [所有选项的列表]
- PlotLegends 的常见设置有:
-
None 没有图例 Automatic 自动确定图例 Placed[lspec,…] 指定图例的放置 - 当采用默认设置 ContourShading->Automatic 时,对 ComplexContourPlot[f,…] 使用色调处理,但不对 ComplexContourPlot[f=g,…] 或 ComplexContourPlot[{f1,f2,…},…] 使用色调处理.
- ComplexContourPlot[{f1==g1,f2==g2,…},…] 叠加显示与等式 fi==gi 关联的所有等值线.
- 在确定如何为等值线之间的区域进行着色时,ComplexContourPlot 首先查看 ContourShading 的显式设置,然后 查看 ColorFunction 的设置.
- 在绘制多个函数的等值线 ComplexContourPlot[{f1,f2,…},…] 时,等值线指定列表 Contours{spec1,spec2,…} 将对每个 fi 使用相应的 speci.
- ColorData["DefaultPlotColors"] 给出 ContourStyle 使用的默认颜色序列.
- ComplexContourPlot 首先在由 PlotPoints 指定的等间隔采样点组成的网格上计算 f. 然后使用一种自适应算法进行至多 MaxRecursion 次子划分,来产生平滑的等值线.
- 应该认识到由于使用的采样点数量有限,ComplexContourPlot 可能会丢失函数的部分特征. 为确保结果正确,可以尝试增大 PlotPoints 和 MaxRecursion 的设置.
- 对于 PerformanceGoal 的某些设置,其它特定选项设置可能会被屏蔽.
- 为 MeshFunctions 和 RegionFunction 中的函数提供的参数为 z、f.
- 只为 ColorFunction 提供一个参数,默认情况下为相邻等值线的缩放过的 f 值的平均值.
- 当采用默认设置 Exclusions->Automatic 和 ExclusionsStyle->None 时,ComplexContourPlot 在它检测到的所有不连续曲线处打破其采样的连续性. 仅当不连续性跳离特定等值线时,该不连续性才立即可见.
- ScalingFunctions 的可能设置包括:
-
sf 缩放 f 值 {sRe,sIm} 缩放实轴和虚轴 {sRe,sIm,sf} 缩放实轴、虚轴及 f 值
所有选项的列表


范例
打开所有单元 关闭所有单元范围 (18)
采样 (6)
用 PlotRange 选取感兴趣的区域:
用 PlotPoints 和 MaxRecursion 控制自适应采样:
用 RegionFunction 将曲面限制在不等式给定的区域上:
用 Exclusions 控制有断点时是否及在何处切割:
选项 (138)
AspectRatio (4)
Axes (4)
BoundaryStyle (3)
BoundaryStyle 也适用于由 RegionFunction 切割出的洞,但不适用于 Exclusions 造成的切割:
用 ExclusionsStyle 替代:
ColorFunctionScaling (1)
ColorFunction 可以使用缩放过的或未经缩放的坐标:
Contours (9)
ContourShading (5)
如果采用自动色调设置,则在数值较小处颜色较深,在数值较大处颜色较浅:
用 None 只显示等值线:
ContourStyle (7)
用 None 隐去等值线:
EvaluationMonitor (2)
Frame (4)
FrameTicks (9)
使用 All 可在所有边上添加刻度标签:
ImageSize (7)
PlotLegends (12)
PlotLegends 自动与颜色函数匹配:
PlotLegendsAutomatic 用占位符值标注等值线:
PlotLegends"Expressions" 用相应的函数标注等值线:
PlotLegendsAutomatic 用占位符值标注隐式曲线:
PlotLegends"Expressions" 用实际的方程式作为图例:
用 Placed 改变图例的位置:
用 BarLegend 改变图例的外观:
ScalingFunctions (5)
Ticks (9)
应用 (23)
Basic Applications (7)
Conformal Maps (6)
倒函数 ![]() 将以原点为中心的圆映射为以原点为中心的圆,并将穿过原点的直线映射为穿过原点的直线,但 Abs[w] 在
将以原点为中心的圆映射为以原点为中心的圆,并将穿过原点的直线映射为穿过原点的直线,但 Abs[w] 在 ![]() 附近变大:
附近变大:
对于保角映射 ![]() ,在
,在 ![]() 平面的交点处正交的曲线在
平面的交点处正交的曲线在 ![]() 平面上的相应交点处也正交:
平面上的相应交点处也正交:
用 InverseFunction 显示保角映射:
Function Growth (1)
Filter and Transfer Functions (4)
具有粘性阻尼的谐振子的微分方程为 y''+γ y'+y=f(t),其中 γ 为阻尼系数,f(t) 为施加的力. 转移函数为 y 的拉普拉斯变换的倒数:
用 ComplexContourPlot 在 ![]() 平面的子集上绘制转移函数,注意两组等高线在
平面的子集上绘制转移函数,注意两组等高线在 ![]() 附近的快速变化:
附近的快速变化:
绘制滤波器的幅值,并观察到滤波器分布在单位圆上的极点之间的间距相等,为 ![]() :
:
属性和关系 (9)
ComplexContourPlot 是 ContourPlot 的特殊情形:
如果有两个或更多函数,ComplexContourPlot 自动隐去着色:
ComplexRegionPlot 在复平面上绘制区域:
ComplexPlot 使用颜色显示函数的自变量和幅值:
使用 ComplexPlot3D 用 ![]() 轴作为幅值:
轴作为幅值:
用 ComplexArrayPlot 绘制复数数组:
使用 ReImPlot 和 AbsArgPlot 在实数上绘制复数值:
使用 ComplexListPlot 显示复数在平面上的位置:
ComplexStreamPlot 和 ComplexVectorPlot 将复数视为方向:
可能存在的问题 (1)
由于 Arg[f] 不能大于 ![]() ,ComplexContourPlot 通常不对分支切割进行渲染:
,ComplexContourPlot 通常不对分支切割进行渲染:
相关指南
-
▪
- 复数可视化
文本
Wolfram Research (2020),ComplexContourPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ComplexContourPlot.html.
CMS
Wolfram 语言. 2020. "ComplexContourPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ComplexContourPlot.html.
APA
Wolfram 语言. (2020). ComplexContourPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ComplexContourPlot.html 年
BibTeX
@misc{reference.wolfram_2025_complexcontourplot, author="Wolfram Research", title="{ComplexContourPlot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ComplexContourPlot.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_complexcontourplot, organization={Wolfram Research}, title={ComplexContourPlot}, year={2020}, url={https://reference.wolfram.com/language/ref/ComplexContourPlot.html}, note=[Accessed: 03-March-2026]}