Expectation
Expectation[expr,xdist]
假定 x 服从概率分布 dist,给出 expr 的期望值.
Expectation[expr,xdata]
假定 x 服从由 data 给定的概率分布,给出 expr 的期望值.
Expectation[expr,{x1,x2,…}dist]
假定 {x1,x2,…} 服从多元分布 dist,给出 expr 的期望值.
Expectation[expr,{x1dist1,x2dist2,…}]
假定 x1、x2、… 独立且服从分布 dist1、dist2、…,给出 expr 的期望值.
Expectation[exprpred,…]
已知 pred,给出 expr 的条件期望值.
更多信息和选项

- Expectation 也称为期望值.
- xdist 可以用 x
 dist
dist dist 或 x \[Distributed]dist 输入.
dist 或 x \[Distributed]dist 输入. - exprpred 可以用 expr
 cond
cond pred 或 expr \[Conditioned]pred 输入.
pred 或 expr \[Conditioned]pred 输入. - 对于一个连续分布 dist,expr 的概率由
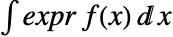 给出,其中
给出,其中 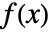 是 dist 的概率密度函数,并且积分在 dist 的定义域上进行.
是 dist 的概率密度函数,并且积分在 dist 的定义域上进行. - 对于一个离散分布 dist,expr 的概率由
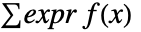 给出,其中
给出,其中 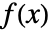 是 dist 的概率密度函数,并且加和在 dist 的定义域上进行.
是 dist 的概率密度函数,并且加和在 dist 的定义域上进行. - 对于数据集 data,expr 的期望值由 Sum[expr,{x,data}]/Length[data] 给出.
- 一元数据以值 {v1,v2,…} 的列表形式给出,多元数据以向量 {{v11,…,v1m},{v21,…,v2m},…} 的列表形式给出.
- Expectation[expr,{x1dist1,x2dist2}] 对应于Expectation[Expectation[expr,x2dist2],x1dist1],因此最后一个变量首先进行加和或积分.
- 如果无法得到符号式期望值,N[Expectation[…]] 将调用 NExpectation. »
- 可以给定下列选项:
-
Assumptions $Assumptions 对参数所做的假定 » GenerateConditions False 是否生成关于参数的条件 Method Automatic 使用何种方法 » TargetUnits Automatic 输出中所显示的单位 »
背景
- Expectation[expr,x] 给出了包含随机变量 x 的表达式 expr 的期望值,假设 x 要么服从一个指定的概率分布(即 是像 NormalDistribution、BinomialDistribution、ChiSquareDistribution 之类的的分布)要么是从给定的数据集中取样(即 是一个数据集)而其中 是 Distributed 的简写. Expectation 的输出可能是一个数或是包含了输入参数的符号表达式.
- Expectation 也可用于多元分布,支持无参数分布如 EmpiricalDistribution、HistogramDistribution 和 KernelMixtureDistribution,以及衍生分布如 TransformedDistribution 和 ProductDistribution. Expectation 也可用于随机过程,包括由 ContinuousMarkovProcess、DiscreteMarkovProcess、WienerProcess 和 PoissonProcess 定义的那些.
- 传入 Expectation 的表达式可以包含线性和非线性的表达式,以及实变量或复变量的函数. Expectation 能计算条件期望,使用形如 exprpred 的表达式即可,其中 是 Conditioned 的简写. Expectation 可以使用许多选项,包括 Assumptions、GenerateConditions 和 Method. Expectation 提供的输出是由包括了符号积分及求和的精确方法计算得出的. 对应的涉及数值方法的结果可用 NExpectation 求得.
- 根据定义,服从分布 的随机变量 x 的期望 Expectation[x,x] 等于其一阶原点矩 Moment[,1] 也因此等于其均值 Mean[]. 此外,配对使用 Expectation 和 Boole 构造得到的 Expectation 的结果也可用 Probability 求得. 例如,Expectation[Boole[1<x<3],xNormalDistribution[]] 其实等价于 Probability[1<x<3, xNormalDistribution[]].
范例
打开所有单元关闭所有单元范围 (31)
基本用途 (9)
如果符号式计算失效,应用 N[Expectation[…]] 来调用 NExpectation:
若无 Assumptions,生成条件:
使用 Assumptions,返回在给定假设下有效的一个结果:
用于数量 (5)
求出使用 QuantityDistribution 指定的期望值:
使用 QuantityMagnitude 计算期望值:
计算由 Quantity 数据给出的分布的期望:
由 QuantityArray 给定的分布:
非参数分布 (4)
使用一个单变量 EmpiricalDistribution,计算期望值:
使用单变量 HistogramDistribution:
使用一个单变量 KernelMixtureDistribution:
使用具有 SurvivalDistribution 的删截数据:
导出分布 (9)
使用 TransformedDistribution 计算期望:
使用 ProductDistribution 求期望值:
选项 (6)
Assumptions (1)
在无 Assumptions 时,生成条件:
如果有 Assumptions,将返回给定假设条件下的有效结果:
Method (4)
利用 Expectation 的积分定义进行运算,速度较慢:
利用 Expectation 作为符号式加和的定义可以得到结果:
求 TukeyLambdaDistribution 中函数的期望值:
期望值可以利用 Quantile 计算:
该例子使用 Integrate:
使用 Activate 计算结果:
TargetUnits (1)
应用 (20)
分布属性 (5)
利用 ParameterMixtureDistribution 直接获得相同的结果:
精算学 (5)
一保险单偿付损失的限额最多为10. 保单持有人的损失 ![]() 所服从分布的密度函数在
所服从分布的密度函数在 ![]() 时为
时为 ![]() ,其它时候为 0. 求该保险单损失支付的期望值:
,其它时候为 0. 求该保险单损失支付的期望值:
一保险公司的月索赔额用一个连续正随机变量 ![]() 模拟,其概率密度函数在
模拟,其概率密度函数在 ![]() 时与
时与 ![]() 成比例. 求该公司月索赔额的期望值:
成比例. 求该公司月索赔额的期望值:
投保房屋的风灾索赔额是相互独立的随机变量,具有的共同密度函数为 ![]() 时为
时为 ![]() ,其余时候为 0,其中
,其余时候为 0,其中 ![]() 是以1000为单位的索赔额. 求最大的三次索赔的期望值:
是以1000为单位的索赔额. 求最大的三次索赔的期望值:
令 ![]() 表示发生事故的一辆投保汽车的年龄. 令
表示发生事故的一辆投保汽车的年龄. 令 ![]() 表示车主在发生事故时对汽车投保的时间长度.
表示车主在发生事故时对汽车投保的时间长度. ![]() 和
和 ![]() 具有联合概率密度函数
具有联合概率密度函数 ![]() (当
(当 ![]() 且
且 ![]() 时),0 (其它情况). 计算发生事故的投保汽车的期望年龄:
时),0 (其它情况). 计算发生事故的投保汽车的期望年龄:
在损失再保险协议的免赔限度下,仅当索赔超出一定金额时,承保人与再承保人共同承担索赔支付. 否则,承保人支付全部索赔. 假定索赔服从参数为 ![]() 和
和 ![]() 的对数正态分布. 计算当保留水平为
的对数正态分布. 计算当保留水平为 ![]() 时,承保人和再承保人索赔金额的期望值
时,承保人和再承保人索赔金额的期望值 ![]() 和
和 ![]() . 求承保人索赔支付的期望值:
. 求承保人索赔支付的期望值:
金融 (2)
计算在时刻 ![]() 支付的1美元死亡恤金的期望时值,其中
支付的1美元死亡恤金的期望时值,其中 ![]() 服从 Gompertz–Makeham分布:
服从 Gompertz–Makeham分布:
求通常在保险单年度的开始支付的年保费,使得 ![]() 期支付流的期望时值等于净整付保费(其中
期支付流的期望时值等于净整付保费(其中 ![]() 服从 Gompertz–Makeham 分布):
服从 Gompertz–Makeham 分布):
股票价格在时刻 ![]() (单位为年)的比例变化
(单位为年)的比例变化 ![]() 假定为参数为
假定为参数为 ![]() 和
和 ![]() 的对数正态分布:
的对数正态分布:
假设投资者可以股息收益率 ![]() ,复利年利率为
,复利年利率为 ![]() 无风险地连续投资一年,风险中性定价条件要求:
无风险地连续投资一年,风险中性定价条件要求:
考虑一个一年后以固定价格 ![]() 购买该股票的期权. 期权的价值等于:
购买该股票的期权. 期权的价值等于:
我们再来考虑一年后以固定价格 ![]() 卖出该股票的期权. 期权的价值为:
卖出该股票的期权. 期权的价值为:
假定利率 ![]() 为 5%,股息收益率为2%,波动参数
为 5%,股息收益率为2%,波动参数 ![]() 为 0.087,每支股票的初始价格为200美元,行使价为每股190美元,则 Black–Scholes 看涨看跌期权价格为:
为 0.087,每支股票的初始价格为200美元,行使价为每股190美元,则 Black–Scholes 看涨看跌期权价格为:
可以将上述结果与 FinancialDerivative 进行比较:
随机试验 (2)
连续分布 ![]() 中样本量为10的随机样本以升序排列. 生成一个新的随机数. 求第11个样本落在排序列表的第4个和第5个最小值之间的概率:
中样本量为10的随机样本以升序排列. 生成一个新的随机数. 求第11个样本落在排序列表的第4个和第5个最小值之间的概率:
求最大的三个值之和的期望值. 利用恒等式 ![]() 和所得到的 Expectation 的线性关系:
和所得到的 Expectation 的线性关系:
属性和关系 (10)
使用 NExpectation 求期望的数值:
利用 Expectation 得到相同的结果:
如果符号计算失败,N[Expectation[…]] 等价于 NExpectation:
用 AsymptoticExpectation 求期望的渐近近似:
用 Asymptotic[Expectation[…]] 获取同样的结果:
Mean、Moment、Variance 和其他属性由期望值定义:
包括 MomentGeneratingFunction 在内的母函数均由期望值定义:
对于一个由列表指定的分布,Expectation 等价于使用 Mean:
可能存在的问题 (1)
默认情况下,Integrate 的 GenerateConditions 设置为 False,Expectation 可能会给出错误的结果:
将 GenerateConditions 设置为 True 以确保正确的结果:
文本
Wolfram Research (2010),Expectation,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Expectation.html (更新于 2016 年).
CMS
Wolfram 语言. 2010. "Expectation." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/Expectation.html.
APA
Wolfram 语言. (2010). Expectation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Expectation.html 年