ExtremeValueDistribution
表示定位参数为 α、尺度参数为 β 的极值分布.
表示一个本地参数为0且尺度参数为1的极值分布.
更多信息

- 极值分布给出从诸如正态分布等分布中抽取的样本中最大值的渐近分布.
- 在极值分布中,值
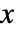 的概率密度和
的概率密度和 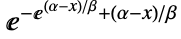 成正比. »
成正比. » - 最小值的渐近分布,有时也称为极值分布,这在 Wolfram 语言中用 GumbelDistribution 实现. »
- ExtremeValueDistribution 中 α 可以为任意实数,β 可以为任意正实数.
- ExtremeValueDistribution 允许 α 和 β 可为任何有相同单位维度的数量. »
- ExtremeValueDistribution 可以和诸如 Mean、CDF 以及 RandomVariate 等函数联用. »
背景
- ExtremeValueDistribution[α,β] 表示一个定义于实数集合上的连续统计分布,参数为实数 α,被称为“定位参数”,以及正实数 β,被称为“尺度参数”. 极值分布的概率密度函数(PDF)的整体行为是光滑的和单峰的,参数 α 和 β 分别决定了 PDF 的水平位置、整体高度和陡峭程度. 此外,对于较大的
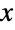 值,由于 PDF 指数式减小,而不是代数式减小,PDF 的尾显得较“细”. (通过分析分布的 SurvivalFunction,这种行为可被定量确定.)极值分布也可以被称为 I 型极值分布、双指数分布(不要与 LaplaceDistribution 相混淆,它也可被称为双指数)、对数韦伯分布 (WeibullDistribution),或是 Gumbel 型分布(不要与 GumbelDistribution 相混淆).
值,由于 PDF 指数式减小,而不是代数式减小,PDF 的尾显得较“细”. (通过分析分布的 SurvivalFunction,这种行为可被定量确定.)极值分布也可以被称为 I 型极值分布、双指数分布(不要与 LaplaceDistribution 相混淆,它也可被称为双指数)、对数韦伯分布 (WeibullDistribution),或是 Gumbel 型分布(不要与 GumbelDistribution 相混淆). - 尽管 ExtremeValueDistribution 有时被冠名为极值分布,但实际上它只是“极值分布”这个大标题所包含的四个分布(其它三个为 GumbelDistribution、FrechetDistribution 和 WeibullDistribution)中的一个. 极值分布是不断增大的随机样本中最大值的极限分布,因为 PDF 的双指数特性(其形式为 Exp[-Exp[…]]),分布的图形呈现出分布中独一无二的属性——更夸张的特征(比如更高的尖峰、更细的尾). 在二十世纪二十年代早期,天文学观测中出现一些比较偏的数据,那么,是利用还是丢弃这些数据,为了解决这个问题推出了极值分布. 该领域中重要的里程碑是极值理论,极值分布被广泛应用于描述“极不可能”的情况(数据集中包含极度偏离中位数的值),比如,特大洪涝灾害、灾难性的保险损失以及大规模的野火. 而且,在生物学中,极值分布作为一种工具,还可以用来对进化过程中的基因突变进行建模.
- RandomVariate 可用来给出一个或更多机器精度或任意精度(后者可通过设置 WorkingPrecision 选项获得)的极值分布中的伪随机变数. Distributed[x,ExtremeValueDistribution[α,β]],更简洁的式子为 xExtremeValueDistribution[α,β],可用来断定随机变量 x 服从极值分布. 它也可以被用在诸如 Probability、NProbability、Expectation 和 NExpectation 这样的函数中.
- 通过使用 PDF[ExtremeValueDistribution[α,β],x] 和 CDF[ExtremeValueDistribution[α,β],x],可以得到极值分布的概率密度和累积分布函数. 可以用 Mean、Median、Variance、Moment 和 CentralMoment 来分别计算均值、中位数、方差、原始矩和中心矩.
- 可以用 DistributionFitTest 来检测一个数据集是否符合极值分布,根据给定数据,用 EstimatedDistribution 来估计参数化极值分布,而 FindDistributionParameters 则可用来将数据拟合成极值分布. 用 ProbabilityPlot 指令可以产生给定数据的 CDF 与符号式极值分布的 CDF 的比较图,QuantilePlot 则能绘制给定数据的分位数和符号式极值分布的分位数的比较图.
- 可以用 TransformedDistribution 来表示转换过的极值分布,用 CensoredDistribution 表示截尾后位于上限和下限值之间的数据的分布,而 TruncatedDistribution 则表示删失后位于上限和下限值之间的数据的分布. CopulaDistribution 可用来构建包含极值分布的高维分布, ProductDistribution 可以计算由独立分布为极值分布所得的联合分布.
- 极值分布与许多其它分布相关. 如前所述,ExtremeValueDistribution 是用来描述极不可能发生的事件的分布之一,其它几个分布包括 GumbelDistribution、FrechetDistribution 和 WeibullDistribution. 这种性质上的关系也包含数量上的成分,ExtremeValueDistribution[α,β] 的 PDF 实际上与 TransformedDistribution[-u,u GumbelDistribution[-α,β]] 和TransformedDistribution[-β α Log[u/β]+α,u WeibullDistribution[α,β]] 的 PDF 一样. ExtremeValueDistribution 可由 ExponentialDistribution 和 MinStableDistribution 转换而来,是 MaxStableDistribution 的一个特例,因为 ExtremeValueDistribution[α,β] 和 MaxStableDistribution[α,β,0] 有相同的 PDF. ExtremeValueDistribution 还与 ExpGammaDistribution、ExponentialDistribution 和 LogisticDistribution 有关.
范例
打开所有单元关闭所有单元范围 (7)
持续在参数中使用 Quantity 会产生 QuantityDistribution:
应用 (3)
ExtremeValueDistribution 可用于模拟月最大风速. 麻省波士顿从 1950 年 1 月至 2009 年 12 月记录的月最大风速(km/h):
属性和关系 (16)
当平移并且使用一个正因子为比例进行缩放时,新生成的分布仍然是极值分布:
偏度是 GumbelDistribution 偏度的负值:
ExtremeValueDistribution 向右偏移,而 GumbelDistribution 向左偏移:
峰度与 GumbelDistribution 相同:
在 Max 下,所得分布仍然是 ExtremeValueDistribution:
ExtremeValueDistribution 的 CDF 求解稳定公设方程:
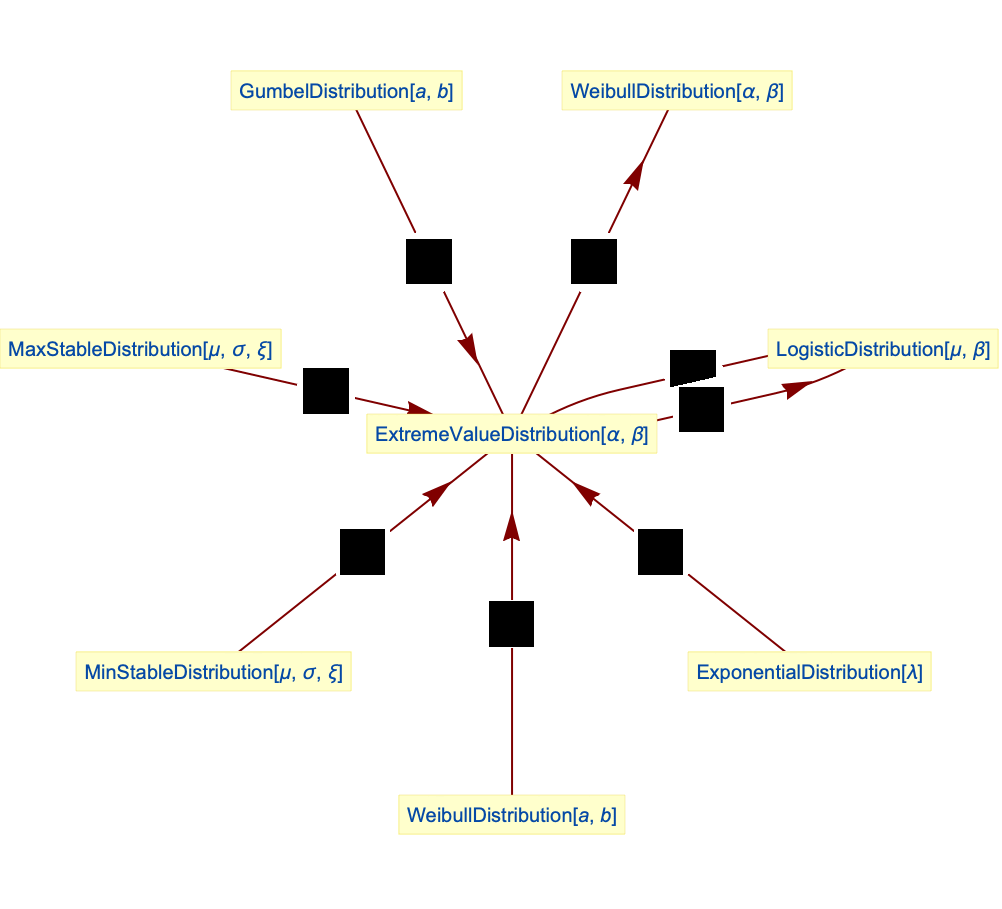
ExtremeValueDistribution 是负的 GumbelDistribution:
ExtremeValueDistribution 是 WeibullDistribution 的一种变换:
WeibullDistribution 是极值分布的一种变换:
极值分布是 MaxStableDistribution 的一个特例:
极值分布是 MinStableDistribution 的一种变换:
极值分布是 ExponentialDistribution 的一种变换:
两个服从极值分布的变量之差所服从的分布与两个服从 GumbelDistribution 的变量之差所服从的分布相同,即 LogisticDistribution:
极值分布和 GumbelDistribution 之和服从 LogisticDistribution:
LogisticDistribution 是一个极值分布的 ParameterMixtureDistribution:
ExponentialDistribution 和 ExtremeValueDistribution 的最大值服从 ShiftedGompertzDistribution:
可能存在的问题 (3)
ExtremeValueDistribution 给出最大值的分布:
GumbelDistribution 给出最小值的分布:
当 α 不是实数时,ExtremeValueDistribution 没有定义:
当 β 不是正实数时,ExtremeValueDistribution 没有定义:
文本
Wolfram Research (2007),ExtremeValueDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2007. "ExtremeValueDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html.
APA
Wolfram 语言. (2007). ExtremeValueDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html 年