FourierTransform
FourierTransform[expr,t,ω]
gives the symbolic Fourier transform of expr.
FourierTransform[expr,{t1,t2,…},{ω1,ω2,…}]
gives the multidimensional Fourier transform of expr.
Details and Options

- The Fourier transform of a function
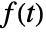 is by default defined to be
is by default defined to be 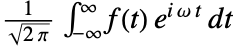 .
. - The multidimensional Fourier transform of a function
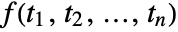 is by default defined to be
is by default defined to be 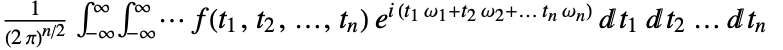 .
. - Other definitions are used in some scientific and technical fields.
- Different choices of definitions can be specified using the option FourierParameters.
- With the setting FourierParameters->{a,b} the Fourier transform computed by FourierTransform is
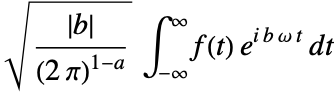 .
. - Some common choices for {a,b} are {0,1} (default; modern physics), {1,-1} (pure mathematics; systems engineering), {-1,1} (classical physics), and {0,-2Pi} (signal processing).
- The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters FourierParameters {0,1} parameters to define the Fourier transform GenerateConditions False whether to generate answers that involve conditions on parameters - FourierTransform[expr,t,ω] yields an expression depending on the continuous variable ω that represents the symbolic Fourier transform of expr with respect to the continuous variable t. Fourier[list] takes a finite list of numbers as input, and yields as output a list representing the discrete Fourier transform of the input.
- In TraditionalForm, FourierTransform is output using ℱ. »
Examples
open allclose allScope (6)
Piecewise functions and distributions:
TraditionalForm formatting:
Options (3)
Assumptions (1)
The Fourier transform of BesselJ is a piecewise function:
FourierParameters (1)
GenerateConditions (1)
Use GenerateConditions->True to get parameter conditions for when a result is valid:
Applications (4)
The power spectrum of a damped sinusoid:
The Fourier transform of a radially symmetric function in the plane can be expressed as a Hankel transform. Verify this relation for the function defined by:
Compute its Fourier transform:
Obtain the same result using HankelTransform:
Generate a gallery of Fourier transforms for a list of radially symmetric functions:
Compute the Hankel transforms for these functions:
Generate the gallery of Fourier transforms as required:
Calculate power spectrum of a stationary OrnsteinUhlenbeckProcess:
Properties & Relations (4)
Use Asymptotic to compute an asymptotic approximation:
FourierTransform and InverseFourierTransform are mutual inverses:
FourierTransform and FourierCosTransform are equal for even functions:
FourierTransform and FourierSinTransform differ by for odd functions:
Possible Issues (1)
Text
Wolfram Research (1999), FourierTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierTransform.html.
CMS
Wolfram Language. 1999. "FourierTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FourierTransform.html.
APA
Wolfram Language. (1999). FourierTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierTransform.html