FourierTransform

FourierTransform[expr,t,ω]

给出 expr 的符号傅里叶变换.

FourierTransform[expr,{t1,t2,…},{ω1,ω2,…}]

给出 expr 的多维傅里叶变换.

更多信息和选项

  • 在缺省情况下，函数 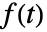的傅里叶变换的定义为 .
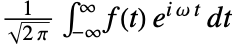  • 缺省情况下，函数 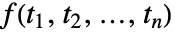的多维傅立叶变换被定义为 .
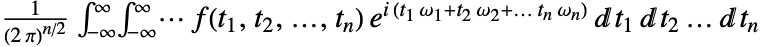  • 其它定义用在一些科学和技术领域中.
  • 不同的定义选择可以使用选项 FourierParameters 指定.
  • 设置 FourierParameters->{a,b}，由 FourierTransform 计算的傅里叶变换是 .
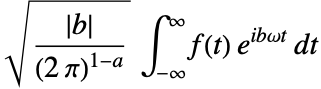  • {a,b} 的某些通用表示形式：{0,1} (缺省：现代物理)，{1,-1} (纯数学；系统工程)， {-1,1} (传统物理)， 以及 {0,-2Pi} (信号处理).
  • 可以给出下列选项：
  • Assumptions $Assumptions所做的参数假定
    FourierParameters {0,1}定义的傅里叶转换的参数
    GenerateConditions False是否产生关于参数条件的结果
  • FourierTransform[expr,t,ω] 产生一个依赖连续变量 ω 的表达式. 该变量表示 expr 的相对于连续变量 t 的符号傅里叶变换. Fourier[list] 取有限数列表作为输入，并产生结果当输出一个表示输入的离散傅里叶变换的列表.
  • 在 TraditionalForm 中，FourierTransform 用 ℱ 输出. »

范例

打开所有单元关闭所有单元

基本范例  (2)

范围  (6)

初等函数：

特殊函数：

分段函数和分布：

周期函数：

多变量函数：

TraditionalForm 格式：

选项  (3)

Assumptions  (1)

BesselJ 的傅里叶变换是分段函数：

FourierParameters  (1)

缺省的现代物理惯例：

纯数学，系统工程的惯例：

传统物理的惯例：

信号处理的惯例：

GenerateConditions  (1)

当结果是有效时，用 GenerateConditions->True 来获得参数条件：

应用  (4)

阻尼正弦曲线的幂频谱：

平面中径向对称函数的傅立叶变换可以表示为汉克尔变换. 验证由下面定义的函数的这种关系：

绘制函数：

计算它的傅立叶变换：

用 HankelTransform 得到同样的结果：

绘制傅立叶变换：

生成一组径向对称函数的傅立叶变换图集：

计算这些函数的汉克尔变换：

生成要求的傅立叶变换图集：

计算平稳 OrnsteinUhlenbeckProcess 的功率谱：

属性和关系  (4)

用 Asymptotic 计算渐近逼近：

FourierTransform 和 InverseFourierTransform 是互逆的：

对奇函数，FourierTransform 和 FourierCosTransform 是相等的：

对偶函数，FourierTransform 和 FourierSinTransform 的差异为 ：

可能存在的问题  (1)

一个逆傅里叶变换的结果可能和初始不相同：

巧妙范例  (1)

加权的 Hermite 多项式的傅里叶变换有非常简单的形式：

Wolfram Research (1999)，FourierTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FourierTransform.html.

文本

Wolfram Research (1999)，FourierTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FourierTransform.html.

CMS

Wolfram 语言. 1999. "FourierTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FourierTransform.html.

APA

Wolfram 语言. (1999). FourierTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FourierTransform.html 年

BibTeX

@misc{reference.wolfram_2024_fouriertransform, author="Wolfram Research", title="{FourierTransform}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/FourierTransform.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fouriertransform, organization={Wolfram Research}, title={FourierTransform}, year={1999}, url={https://reference.wolfram.com/language/ref/FourierTransform.html}, note=[Accessed: 05-November-2024 ]}