IdentityMatrix
nn の恒等行列を与える.
IdentityMatrix[{m,n}]
mn の恒等行列 を与える.
詳細とオプション


- 恒等行列は,正方行列の乗算の単位元である.
- 恒等行列
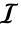 の成分は
の成分は ![I〚i,j〛=TemplateBox[{{i, ,, j}}, KroneckerDeltaSeq] I〚i,j〛=TemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]](Files/IdentityMatrix.ja/3.png) で与えられる.つまり,対角成分が1でそれ以外は0ということである.
で与えられる.つまり,対角成分が1でそれ以外は0ということである. - nn 恒等行列 ℐ は,任意の nn 行列 m について,関係 m.ℐ=ℐ.m=m を満足する.
- nn 等行列は,対称,正定値,ユニタリ行列であり,mn 恒等行列はユニタリ行列である.
- IdentityMatrixは,デフォルトで,厳密な整数を含む行列を作る.
- IdentityMatrix[…,SparseArray]は,恒等行列をSparseArrayオブジェクトとして与える.
- 次は,使用可能なオプションである.
-
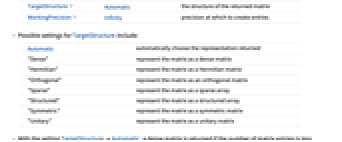
TargetStructure Automatic 返される行列の構造 WorkingPrecision Infinity 成分を作成する際の精度 - 次は,TargetStructureの可能な設定である.
-
Automatic 返す際の表現を自動選択する "Dense" 行列を密な行列として表す "Hermitian" 行列をエルミート(Hermite)行列として表す "Orthogonal" 行列を直交行列として表す "Sparse" 行列を疎な行列として表す "Structured" 行列を構造化配列として表す "Symmetric" 行列を対称行列として表す "Unitary" 行列をユニタリ行列として表す - TargetStructureAutomaticの設定では,行列の成分数が設定された閾値未満の場合は密な行列が返され,それ以外の場合は構造化配列が返される.
- 恒等行列は,構造化配列として返される場合は,効率的な格納とDet,Dot,Inverse,LinearSolve等のより効率的な操作を可能にする.
- 次は,IdentityMatrixで加速される操作である.
-
Det 時間 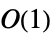
Dot 時間 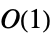
Inverse 時間 
LinearSolve 時間 
- 構造化されたIdentityMatrix id は,次の特性"prop"に id["prop"]でアクセスできる.
-
"WorkingPrecision" 内部精度 "Properties" サポートされる特性のリスト "Structure" 構造化配列の型 "StructuredData" 構造化配列で保存されている内部データ "StructuredAlgorithms" 構造化配列に対して特別なメソッドを持つ関数のリスト "Summary" Datasetとして表される要約情報 - Normal[IdentityMatrix[…]]は恒等行列を通常の行列として与える.

例題
すべて開くすべて閉じるスコープ (6)
オプション設定TargetStructure"Sparse"を使って疎な恒等行列を構築する:
大きい行列の場合,疎な表現を使うとメモリが大幅に節約できる:
オプション設定TargetStructure"Structured"を使って構造化恒等行列を生成する:
IdentityMatrixオブジェクトは配列についての情報を与える特性がある:
"WorkingPrecision"は行列成分の精度を与える:
オプション (7)
TargetStructure (5)
TargetStructureAutomaticの設定のときは,小さい次元については密な行列が返される:
アプリケーション (3)
IdentityMatrixを使って標準基底を![]() 上にすばやく定義する:
上にすばやく定義する:
IdentityMatrixを使って固有多項式を計算する:
CharacteristicPolynomialを使って直接計算したものと比較する:
拡大行列の行を削減するとInverse[m]で拡大された恒等行列が与えられる:
r の右半分が真にInverse[m]であることを確認する:
特性と関係 (15)
正方恒等行列はそれ自身の逆行列であり,それ自身の転置でもある:
恒等行列の ![]()
![]() ,
, ![]()
![]() 番目の項目はKroneckerDelta[i,j]で与えられる:
番目の項目はKroneckerDelta[i,j]で与えられる:
IdentityMatrix[n]の ![]() 番目の行または列はUnitVector[n,i]である:
番目の行または列はUnitVector[n,i]である:
IdentityMatrix[{n,m}]については,i≤Min[n,m]のとき行はUnitVector[m,i]である:
IdentityMatrixは構造化DiagonalMatrixに変換できる:
一般的な対角行列にDiagonalMatrixを使う:
可逆な n×n 行列 m については,Inverse[m].m==m.Inverse[m]==IdentityMatrix[n]である:
n×m 行列 a については,a.PseudoInverse[a]==IdentityMatrix[n]である:
非特異 n×n 行列 m については,MatrixPower[m,0]==IdentityMatrix[n]である:
行列と恒等行列のKroneckerProductはブロック対角行列である:
WorkingPrecisionオプションは行列を作り次にNを適用するのと等しい:
IdentityMatrix が正方行列なら,PermutationMatrixに変換できる:
テキスト
Wolfram Research (1988), IdentityMatrix, Wolfram言語関数, https://reference.wolfram.com/language/ref/IdentityMatrix.html (2024年に更新).
CMS
Wolfram Language. 1988. "IdentityMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/IdentityMatrix.html.
APA
Wolfram Language. (1988). IdentityMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IdentityMatrix.html