InverseFourierCosTransform

InverseFourierCosTransform[expr,ω,t]

给出 expr 的符号傅立叶余弦逆变换.

InverseFourierCosTransform[expr,{ω1,ω2,…},{t1,t2,…}]

给出 expr 的多维傅立叶余弦逆变换.

更多信息和选项

  • The Fourier cosine transform is a particular way of viewing the Fourier transform without the need for complex numbers or negative frequencies.
  • Joseph Fourier designed his famous transform using this and the Fourier sine transform, and they are still used in applications like signal processing, statistics and image and video compression.
  • The inverse Fourier cosine transform of the frequency domain function 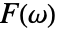is the time domain function 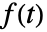for :
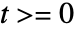  • 一个函数 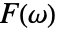的傅立叶余弦逆变换在缺省情况下定义成 .
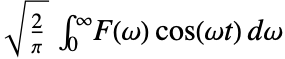  • The multidimensional inverse Fourier cosine transform of a function 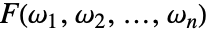is by default defined as 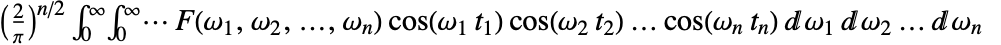or when using vector notation, (2/pi)^(n/2)int_(omega in TemplateBox[{}, PositiveReals]^n)F(omega) cos(omega t)domega.
  • 不同的定义选择可以用选项 FourierParameters 指定.
  • The integral is computed using numerical methods if the third argument, 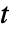, is given a numerical value.
  • The asymptotic inverse Fourier cosine transform can be computed using Asymptotic.
  • There are several related Fourier transformations:
  • FourierTransforminfinite continuous-time functions (FT)
    FourierSequenceTransforminfinite discrete-time functions (DTFT)
    FourierCoefficientfinite continuous-time functions (FS)
    Fourierfinite discrete-time functions (DFT)
  • The inverse Fourier cosine transform is an automorphism in the Schwartz vector space of functions whose derivatives are rapidly decreasing and thus induces an automorphism in its dual: the space of tempered distributions. These include absolutely integrable functions, well-behaved functions of polynomial growth and compactly supported distributions.
  • Hence, InverseFourierCosTransform not only works with absolutely integrable functions on 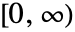, but it can also handle a variety of tempered distributions such as DiracDelta to enlarge the pool of functions or generalized functions it can effectively transform.
  • The lower limit of the integral is effectively taken to be TemplateBox[{0, -}, Superscript], so that the inverse Fourier cosine transform of the Dirac delta function 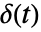is equal to . »
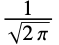  • The following options can be given:
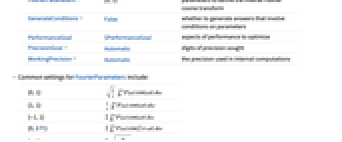
  • AccuracyGoal Automaticdigits of absolute accuracy sought
    Assumptions $Assumptionsassumptions to make about parameters
    FourierParameters {0,1}parameters to define the inverse Fourier cosine transform
    GenerateConditions Falsewhether to generate answers that involve conditions on parameters
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoal Automaticdigits of precision sought
    WorkingPrecision Automaticthe precision used in internal computations
  • Common settings for FourierParameters include:
  • {0,1}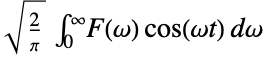
    {1,1}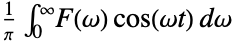
    {-1,1}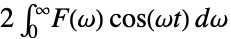
    {0,2Pi}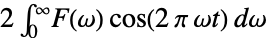
    {a,b}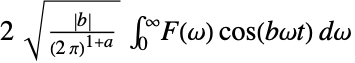

范例

打开所有单元关闭所有单元

基本范例  (6)

Compute the inverse Fourier cosine transform of a function:

Plot the function and its inverse cosine transform:

Inverse Fourier cosine transform of reciprocal square root:

For a different convention, change the parameters:

Inverse Fourier cosine transform of a Gaussian is another Gaussian:

Plot both Gaussians:

Compute the inverse Fourier cosine transform of a multivariate function:

Plot the result:

Compute the inverse transform at a single point:

范围  (43)

Basic Uses  (3)

Inverse Fourier cosine transform of a function for a symbolic parameter :

Inverse Fourier cosine transforms involving trigonometric functions:

Plot the transform:

Plot the transform for :

Evaluate the inverse Fourier cosine transform for a numerical value of the parameter :

Algebraic Functions  (4)

Inverse Fourier cosine transform of power functions:

For integer , the result is a derivative of DiracDelta:

Inverse cosine transforms for rational functions:

Plot the transform:

Plot the transform:

Inverse Fourier cosine transform of a quotient of two nonlinear polynomials:

Plot the transform:

Inverse Fourier cosine transform of a quotient of quadratic and quartic polynomials:

Plot the transform:

Exponential and Logarithmic Functions  (4)

Inverse Fourier cosine transforms of exponential functions:

Transform for :

Plot the transform:

Inverse Fourier cosine transform of a Gaussian being itself:

Plot the transform:

Inverse Fourier cosine transforms of products of exponential and trigonometric functions:

Plot the transform for and :

Plot the transform:

Inverse cosine transforms of logarithmic functions:

Plot the transform:

Plot the transform:

Plot the transform:

Plot the transform:

Trigonometric Functions  (5)

Expressions involving trigonometric functions:

Plot the transform:

Composition of elementary functions:

Plot the transform for :

Ratio of sine and product of exponential and linear functions:

Plot the transform:

Inverse Fourier cosine transforms of arctangent functions:

Plot the transform:

Plot the transform:

Inverse Fourier cosine transform of Sech is another Sech:

Plot the transform:

Special Functions  (9)

Sinc function:

Plot the transform:

Inverse Fourier cosine transforms of expressions involving ExpIntegralEi:

Plot the transform:

Plot the transform:

Expression involving Erfc:

Plot the transform for :

Expression involving SinIntegral:

Plot the transform:

CosIntegral:

Plot the transform:

Inverse cosine transforms for BesselJ functions:

Plot the transform for :

Plot the transform for and :

Plot the transform for and :

Plot the transform:

Cosine transforms for BesselY functions:

Plot the transform for :

Plot the transform for and :

Cosine transform for a BesselK function:

Plot the transform:

Inverse cosine transform for a hypergeometric function is a BesselK function:

Plot the transform:

Piecewise Functions and Distributions  (4)

Inverse Fourier cosine transform of a piecewise function:

Restriction of a sine function to a half-period:

Triangular function:

Transforms in terms of FresnelC:

Plot the transform:

Plot the transform:

Periodic Functions  (2)

Inverse Fourier cosine transform of cosine:

Inverse Fourier cosine transform of SquareWave:

Generalized Functions  (4)

Inverse Fourier cosine transforms of expressions involving HeavisideTheta:

Inverse Fourier cosine transform involving DiracDelta:

Plot the transform:

Plot the transform:

Plot the transform:

Inverse Fourier cosine transform involving HeavisideLambda:

Inverse Fourier cosine transform involving HeavisidePi:

Multivariate Functions  (3)

Inverse Fourier cosine transform of rational function in two variables:

Plot of both:

Inverse Fourier cosine transform of exponential in two variables:

Plot of both:

Inverse Fourier cosine transform of product of exponential and SquareWave:

Formal Properties  (3)

Inverse Fourier cosine transform of a first-order derivative:

Inverse Fourier cosine transform of a second-order derivative:

Inverse Fourier cosine transform threads itself over equations:

Numerical Evaluation  (2)

Calculate the inverse Fourier cosine transform at a single point:

Alternatively, calculate the Fourier cosine transform symbolically:

Then evaluate it for specific value of :

选项  (8)

AccuracyGoal  (1)

The option AccuracyGoal sets the number of digits of accuracy:

With default settings:

Assumptions  (1)

用 Assumptions 定来指定感兴趣的参数区域：

FourierParameters  (3)

Inverse Fourier cosine transform for the unit box function with different parameters:

不同定义的变换，用非缺省的转换：

To get the original function back, use the same FourierParameters setting:

Set up your particular global choice of parameters to work once per session:

Restore defaults:

GenerateConditions  (1)

当结果有效时，用 GenerateConditions->True 获得参数条件：

PrecisionGoal  (1)

The option PrecisionGoal sets the relative tolerance in the integration:

With default settings:

WorkingPrecision  (1)

If a WorkingPrecision is specified, the computation is done at that working precision:

With default settings:

应用  (4)

Ordinary Differential Equations  (1)

Consider the following ODE with initial condition :

Apply the Fourier cosine transform to the ODE:

Solve for the Fourier cosine transform of :

Find the inverse Fourier cosine transform with and :

Compare with DSolveValue:

Partial Differential Equations  (1)

Solve the heat equation for , : with initial condition for and Neumann boundary condition for :

Apply the Fourier cosine transform to the ODE on :

With and , solve this ODE:

Compute the inverse cosine transform of the exponential functions:

Convolution property gives the inverse cosine transform of the first summand to get the solution:

Consider the special case with , and :

Compare with DSolveValue:

Plot the initial conditions and solutions for different values of .

Evaluation of Integrals  (2)

Calculate the following definite integral:

Inverse Fourier cosine transform preserves integration of products over :

Solve the definite integral:

Compare with Integrate:

Calculate the following definite integral for :

Compute inverse fourier cosine transform of the square root of the integrand:

Apply Parseval's identity:

Or equivalently:

Solve for the definite integral:

Compare with Integrate:

属性和关系  (4)

By default, the inverse Fourier cosine transform of is:

For , the definite integral becomes:

Compare with InverseFourierCosTransform:

用 Asymptotic 计算渐近近似：

FourierCosTransform 和 InverseFourierCosTransform 是互逆的：

For even functions results are identical to InverseFourierTransform:

结果对于 是一致的：

可能存在的问题  (1)

The result from a Fourier cosine transform may not have the same form as the original:

傅立叶余弦逆变换可能需要类似 DiracDelta 的广义函数：

巧妙范例  (2)

Inverse Fourier cosine transform as a Meijer function:

Create a table of basic inverse Fourier cosine transforms:

Wolfram Research (1999)，InverseFourierCosTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/InverseFourierCosTransform.html （更新于 2025 年）.

文本

Wolfram Research (1999)，InverseFourierCosTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/InverseFourierCosTransform.html （更新于 2025 年）.

CMS

Wolfram 语言. 1999. "InverseFourierCosTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2025. https://reference.wolfram.com/language/ref/InverseFourierCosTransform.html.

APA

Wolfram 语言. (1999). InverseFourierCosTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InverseFourierCosTransform.html 年

BibTeX

@misc{reference.wolfram_2025_inversefouriercostransform, author="Wolfram Research", title="{InverseFourierCosTransform}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/InverseFourierCosTransform.html}", note=[Accessed: 31-January-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_inversefouriercostransform, organization={Wolfram Research}, title={InverseFourierCosTransform}, year={2025}, url={https://reference.wolfram.com/language/ref/InverseFourierCosTransform.html}, note=[Accessed: 31-January-2025 ]}