MoonPosition

✖
`MoonPosition`

✖

MoonPosition[]

gives the position of the Moon for the current date and location.

✖

MoonPosition[datespec]

gives the position of the Moon for the specified date.

✖

MoonPosition[locationspec]

gives the position of the Moon for the specified location.

✖

MoonPosition[locationspec,datespec]

gives the position of the Moon for the specified date and location.

✖

MoonPosition[{{location₁,date₁},{location₂,date₂},…}]

gives the positions of the Moon for all specified locations on the specified dates.

✖

MoonPosition[locationspec,datespec,func]

uses func to determine what to return for extended locations.

Details and Options

MoonPosition returns the coordinates of the Moon on the celestial sphere as observed on any date from any location on Earth.
MoonPosition[] makes use of $GeoLocation and $TimeZone to determine your location and time zone.
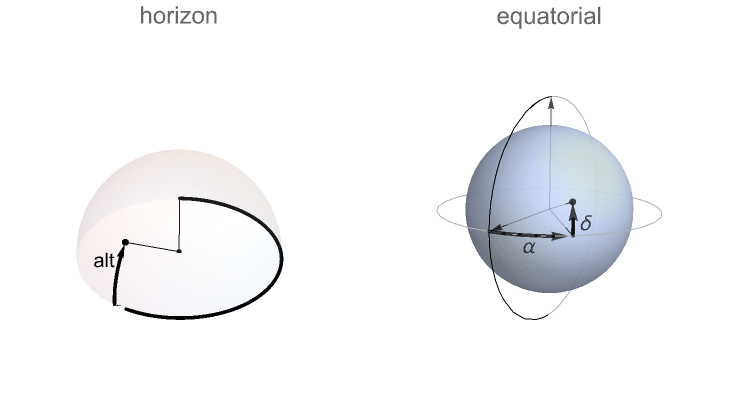
The default form of the results is in the form {azimuth,altitude}.
Locations can be specified as Entity objects, assuming they represent objects with geographic coordinates or GeoGraphics primitives, or they can be latitude/longitude pairs, assuming degrees as units.
datespec can be a DateObject expression, a TimeObject expression, a date string or a {y,m,d,h,m,s} date list.
datespec is assumed to be in $TimeZone, unless it is a DateObject or TimeObject expression with an explicit TimeZone option value.
locationspec and datespec can be either individual items or lists of individual items.
If datespec is a list of dates, then the results will contain TimeSeries objects.
datespec can be specified as {start,end,increment} for compatibility with DateRange specifications.
MoonPosition[…,func] is used to specify the format of output when locations are specified.
Possible settings for func include:

	Automatic	returns intervals for extended locations only
	Interval	returns intervals for all specified locations
	Mean	returns mean value for extended locations
	Min	returns minimum values for extended locations
	Max	returns maximum values for extended locations
	StandardDeviation	returns standard deviation for extended locations

MoonPosition[CelestialSystem->"Equatorial"] gives the right ascension and declination of the Moon.
MoonPosition can accept the following options:

	AltitudeMethod	"ApparentAltitude"	whether to take atmospheric refraction into account when computing altitude
	CelestialSystem	"Horizon"	whether to return azimuth/altitude or right ascension/declination

Possible settings for CelestialSystem include:
"Horizon" returns results as a pair of azimuth/altitude (az/alt) values

"Equatorial" returns results as a pair of right ascension/declination (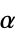/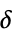) values

Possible settings for AltitudeMethod include:

	"ApparentAltitude"	take atmospheric refraction into account for altitude computations
	"TrueAltitude"	assume no atmospheric refraction for altitude computations

Examples

open allclose all

Basic Examples (5)Summary of the most common use cases

Compute the current position of the Moon for your location:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-etsbfd

Out[1]=1

Compute the position of the Moon for a specified date:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-dans15

Out[1]=1

Compute the current position of the Moon for a specified location:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-19a7o

Out[1]=1

Compute the position of the Moon for a specified latitude/longitude and date:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-k5huuj

Out[1]=1

Compute the position of the Moon for a specified city and date:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-bild8d

Out[1]=1

Scope (8)Survey of the scope of standard use cases

Dates (3)

Dates can be specified as a DateObject:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-slp3xb

Out[1]=1

Dates can be specified as a date string:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-zbahi

Out[1]=1

Generate the Moon's position for a range of dates:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-glueuf

Out[1]=1

Locations (5)

Locations can be latitude/longitude pairs:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-mmgexd

Out[1]=1

Cities are treated as single, specific locations:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-gzg19x

Out[1]=1

Results for extended locations are intervals, by default:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-dtmpwg

Out[1]=1

The form of the results for extended locations can be overridden:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-i1bmkv

Out[1]=1

Find the Moon's position for multiple locations:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-bkoy4c

Out[1]=1

Options (2)Common values & functionality for each option

CelestialSystem (1)

Find the right ascension and declination of the Moon for your location:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-ckrn5

Out[1]=1

AltitudeMethod (1)

The default setting for AltitudeMethod simulates atmospheric refraction:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-bb4dj

Out[1]=1

Allow for no atmospheric refraction when computing the altitude of the Moon:

In[2]:=2

✖

https://wolfram.com/xid/0d6er9h0a6-dmkuu1

Out[2]=2

Applications (4)Sample problems that can be solved with this function

The Moon's orbit is tilted with respect to the Earth's equator:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-gsnuda

Out[1]=1

Plot the angular distance between the Sun and Moon over a month:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-b9odho

In[2]:=2

✖

https://wolfram.com/xid/0d6er9h0a6-8lc3s

In[3]:=3

✖

https://wolfram.com/xid/0d6er9h0a6-j33fj5

In[4]:=4

✖

https://wolfram.com/xid/0d6er9h0a6-il47d

In[5]:=5

✖

https://wolfram.com/xid/0d6er9h0a6-d9u6ck

Out[5]=5

Reconstruct the Moon's orbital period using the position of the Moon over several months:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-bf0irw

Extract the positions where the Moon's right ascension suddenly goes from 24 hours to 0 hours and find the mean period where this transition happens:

In[2]:=2

✖

https://wolfram.com/xid/0d6er9h0a6-f3kpab

Out[2]=2

Compare this to the actual value of the Moon's orbital period:

In[3]:=3

✖

https://wolfram.com/xid/0d6er9h0a6-fvyqvy

Out[3]=3

Plot the position of the Sun and Moon on the celestial sphere:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-brlq2l

In[2]:=2

✖

https://wolfram.com/xid/0d6er9h0a6-b8wfwc

Out[2]=2

Properties & Relations (4)Properties of the function, and connections to other functions

By default, location is specified by $GeoLocation and the date is specified by the current date:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-x72irg

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0d6er9h0a6-cx7drs

Out[2]=2

Results are in the form of a TimeSeries when a range of dates is specified:

In[1]:=1

✖

https://wolfram.com/xid/0d6er9h0a6-rfwbr

Out[1]=1

Results are multivalued for each date specification, so plotting the results using DateListPlot will result in two curves, one for azimuth and one for altitude:

In[1]:=1