NMinimize
NMinimize[f,x]
x について f の数値的最小値を求める.
NMinimize[f,{x,y,…}]
x, y, …について f の数値的最小値を求める.
NMinimize[{f,cons},{x,y,…}]
制約条件 cons 下で f の数値的最小値を求める.
NMinimize[…,x∈rdom]
x が領域 rdom 内にあるように制限する.
詳細とオプション




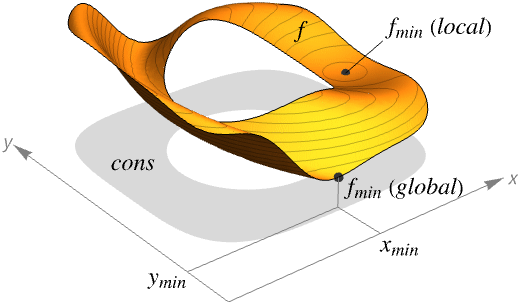
- NMinimizeは大域的最適化(GO)としても知られている.
- NMinimizeは,与えられた制約条件に従って常に f の最小値を求めようとする.
- NMinimizeは,通常,制約が与えられた場合に可能な最小値を求めるために使われる.分野によっては,最適な戦略,最良適合,最適な構成等と呼ばれることがある.
- NMinimizeは{fmin,{x->xmin,y->ymin,…}}の形のリストを返す.
- f および cons が線形または凸のとき,NMinimizeが与える結果は実数および整数値の両方の上で最小値になる.それ以外の場合は結果が単に極小値であるかもしれない.
- NMinimizeが制約条件を満足できないと判断した場合は{Infinity,{x->Indeterminate,…}}が返される.
- NMinimizeは,目的関数 f と制約条件 cons がスカラー変数またはベクトル変数に依存する式で与えられるモデリング言語をサポートする.f と cons は,一般に,非常に効率的な形に解析されるが,f と cons の項が変数の数値に対して数値を与える限りNMinimizeはしばしば解を求めることができる.
- 制約条件 cons は以下の論理結合でよい.
-
lhs==rhs 等式 lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs 不等式 (LessEqual, …) lhsrhs, lhsrhs, lhsrhs, lhsrhs ベクトル不等式 (VectorLessEqual, …) {x,y,…}∈reg 領域指定 - NMinimize[{f,cons},x∈rdom]は,事実上,NMinimize[{f,cons&&x∈rdom},x]に等しい.
- x∈rdom については,Indexed[x,i]を使って別の座標に言及することができる.
- 次は,使用可能な領域 rdom である.
-
Reals 実数スカラー変数 Integers 整数スカラー変数 Vectors[n,dom] 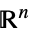 のベクトル変数
のベクトル変数Matrices[{m,n},dom] 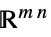 の行列変数
の行列変数ℛ 幾何学領域 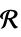 に制限されたベクトル変数
に制限されたベクトル変数 - デフォルトでは,すべての変数が実数であると仮定される.
- 指定可能なオプション
-
AccuracyGoal Automatic 目標となる最終確度桁数 EvaluationMonitor None f が評価されたときに常に評価される式 MaxIterations Automatic 使用する最大反復回数 Method Automatic 使用されるアルゴリズム PrecisionGoal Automatic 目標となる最終精度桁数 StepMonitor None ステップを取るたびに常に評価される式 WorkingPrecision MachinePrecision 内部計算に使用する精度 - AccuracyGoalとPrecisionGoalの設定で最小値の位置の値と最小になったときの関数の値の両方で目標とする桁数を指定する.
- NMinimizeはAccuracyGoalとPrecisionGoalで指定された目標値のどちらかが達成されるまで計算を続ける.
- NMinimizeのためのメソッドには2つのクラスがある.最初のクラスは問題の特性を使うので,メソッドが収束する際に求まった最小値は大域的であることが保証される.2番目のクラスは発見的なメソッドで,複数の局所探索を使うことがあるが,一般的には確率論によって調整され,大域的最小値に焦点が当てられる.このメソッドもしばしば大域的な最小値を求めるが,必ずそうするとは保証されない.
- 次は,解に収束する場合に最小値を与えることが保証されているメソッドである.
-
"Convex" 凸法だけを使う "MOSEK" 凸問題用の商用MOSEKライブラリを使う "Gurobi" 凸問題用の商用Gurobiライブラリを使う "Xpress" 凸問題用の商用Xpressライブラリを使う - 次は,発見的な方法である.
-
"NelderMead" Nelder・Meadのシンプレックス法 "DifferentialEvolution" 差分進化を使う "SimulatedAnnealing" 焼きなまし法を使う "RandomSearch" 複数のランダムな初期点から始めて求まった最良の極小値を使う "Couenne" 非凸混合整数非線形問題にCouenneライブラリを使用する
例題
すべて開くすべて閉じるスコープ (40)
基本的な用法 (12)
いくつかの線形不等式条件はVectorGreaterEqualで表すことができる:
![]() v>=
v>=![]() または \[VectorGreaterEqual]を使ってベクトル不等式の記号を入力する:
または \[VectorGreaterEqual]を使ってベクトル不等式の記号を入力する:
![]() にスレッディングの可能性があるので,不等式
にスレッディングの可能性があるので,不等式 ![]() は
は ![]() とは等しくないかもしれない:
とは等しくないかもしれない:
![]() での意図しないスレッディングを避けたければInactive[Plus]を使うとよい:
での意図しないスレッディングを避けたければInactive[Plus]を使うとよい:
定数パラメータを持つ方程式を使って ![]() での意図しないスレッディングを回避する:
での意図しないスレッディングを回避する:
VectorGreaterEqualは"NonNegativeCone"についての錐不等式を表す:
円錐の次元を明示的に指定したければ,{"NonNegativeCone",n}を使うとよい:
"NormCone"で錐不等式を使って制約条件 ![]() を指定する:
を指定する:
Indexedを使ってベクトル変数の成分(例:![]() )にアクセスする:
)にアクセスする:
ベクトル変数の次元と領域が曖昧なときはVectors[n,dom]を使って指定する:
NonNegativeReals (![]() )を使って非負の制約条件を指定する:
)を使って非負の制約条件を指定する:
NonPositiveReals (![]() )を使って非正の制約条件を指定する:
)を使って非正の制約条件を指定する:
Orという条件を指定することができる:
領域制約1 (4)
Integersを使って整数領域の制約を指定する:
Vectors[n,Integers]を使ってベクトル変数に整数領域の制約を指定する:
NonNegativeIntegers (![]() )を使って非負の整数領域の制約を指定する:
)を使って非負の整数領域の制約を指定する:
NonPositiveIntegers (![]() )を使って非正の整数領域の制約を指定する:
)を使って非正の整数領域の制約を指定する:
領域制約2 (5)
Circumsphereを使うと,同じ結果が直接与えられる:
線形問題 (5)
線形の目的関数と制約条件がある場合は,最小値が見付かるとそれは大域的になる:
Equalを使っていくつかの等式制約を一度に表現する:
VectorLessEqualを使っていくつかのLessEqual不等式制約を一度に表現する:
Intervalを使って変数の境界を指定する:
凸問題 (7)
凸に変換可能 (4)
面積が1で縦が最大でも横の1/2になるようにして長方形の外周を最小化する:
この問題は対数凸関数で,変換{hExp[],wExp[ ]}を行なって対数を取って凸問題を得ることで解くことができる:
不等式制約とノルム制約に従って擬似凸関数![]() を最小化する.目的関数は領域上の非負の関数と非正の関数の積なので,擬似凸関数である:
を最小化する.目的関数は領域上の非負の関数と非正の関数の積なので,擬似凸関数である:
擬似凸問題はパラメータ ![]() についてのパラメトリック凸最適化問題として解くことができる:
についてのパラメトリック凸最適化問題として解くことができる:
制約条件![]() に従って
に従って ![]() を最小化する.目的関数は凸関数ではないが凸関数の差
を最小化する.目的関数は凸関数ではないが凸関数の差 ![]() で表すことができる.ただし,
で表すことができる.ただし,![]() と
と ![]() は凸関数である:
は凸関数である:
制約条件![]() に従って
に従って ![]() を最小化する.制約条件
を最小化する.制約条件![]() が凸ではないが凸制約条件
が凸ではないが凸制約条件 ![]() の差で表すことができる.ただし,
の差で表すことができる.ただし,![]() と
と ![]() は凸関数である:
は凸関数である:
オプション (10)
AccuracyGoalとPrecisionGoal (2)
Method (5)
StepMonitor (1)
古典的なRosenbrock関数の最小値を求める際にNMinimizeが取ったステップ:
WorkingPrecision (1)
作業精度を![]() にする.デフォルトでAccuracyGoalとPrecisionGoalは
にする.デフォルトでAccuracyGoalとPrecisionGoalは![]() に設定されている:
に設定されている:
アプリケーション (19)
幾何学の問題 (4)
![]() と
と ![]() を中心とする半径1の2つの円板間の最短距離を求める.
を中心とする半径1の2つの円板間の最短距離を求める.![]() を円板1の上の点,
を円板1の上の点,![]() 円板2の上の点とする.目的は制約条件
円板2の上の点とする.目的は制約条件![]() に従って
に従って![]() を最小化することである:
を最小化することである:
包み込む最小の球はBoundingRegionを使って効率的に求めることができる:
3Dの点集合を体積を最小にして包み込む,![]() とパラメータ化できる最小の楕円体を求める:
とパラメータ化できる最小の楕円体を求める:
境界楕円体(体積は必ずしも最小ではない)もBoundingRegionを使って求めることができる:
半径 ![]() (
(![]() )の重なり合ない
)の重なり合ない ![]() 個の円が入る最小の正方形を求める.円の数と各円の半径を指定する:
個の円が入る最小の正方形を求める.円の数と各円の半径を指定する:
データフィッティング問題 (3)
与えられた行列 a とベクトル b について,![]() を制約条件
を制約条件 ![]() に従って最小にする:
に従って最小にする:
データの最初と最後の点が曲線上にあるようにして,三次曲線を離散データにフィットする:
DesignMatrixを使って行列を構築する:
最初と最後の点が必ず曲線上にあるように,制約条件を定義する:
分類問題 (5)
分離するためには,集合1は ![]() を,集合2は
を,集合2は ![]() を満足しなければならない:
を満足しなければならない:
目的は ![]() と
と ![]() の間の厚みの2倍を与える
の間の厚みの2倍を与える![]() を最小化することである:
を最小化することである:
DesignMatrixを使って2つの集合のための二次多項式データ行列を構築する:
分離するためには,集合1は ![]() を集合2は
を集合2は ![]() を満足しなければならない:
を満足しなければならない:
与えられた点集合 ![]() を分離して別の集合にする.これは,
を分離して別の集合にする.これは,![]() を最小化して各群の中心
を最小化して各群の中心 ![]() を求めることで行える.ただし,
を求めることで行える.ただし,![]() は与えられた局所カーネル,
は与えられた局所カーネル,![]() は与えられたペナルティパラメータである:
は与えられたペナルティパラメータである:
カーネル ![]() は,
は,![]() でそれ以外は
でそれ以外は ![]() となるような
となるような ![]() -最近傍 (
-最近傍 (![]() ) 関数である.この問題のために
) 関数である.この問題のために ![]() の最近傍が選択されている:
の最近傍が選択されている:
各データ点に対応する中心がある.同じ群に属するデータは同じ中心値を持つ:
正の整数のリストを与えられたときに,このリストを重なり合ない2つの部分集合に分割する.ただし,2つの部分集合の合計の差を最小にしなければならない.リストを定義する:
値が–1か1であるバイナリ変数を定義する.リストの要素が部分集合1に属するなら,これに関連付けられたバイナリ変数の値は–1になる.部分集合2に関連付けられたバイナリ変数は1である:
重さが異なるオブジェクトの集合と2つの袋が与えられたとして,袋の可搬重量を超えない範囲で合計重量が最大になるように2つの袋に入れられるオブジェクトを求める.オブジェクトの数と重さを求める:
オブジェクトを袋1に入れるか,袋2に入れるか,あるいはどちらでもないかを決定するためにバイナリ変数を使用する:
目的は,2つの袋に入るオブジェクトの重さを最大にすることである:
バイナリ変数 ![]() は袋1に入るオブジェクトに関連付けられる.変数
は袋1に入るオブジェクトに関連付けられる.変数 ![]() は
は ![]() の補集合である.袋に入ったオブジェクトの重さは以下の通りである:
の補集合である.袋に入ったオブジェクトの重さは以下の通りである:
画像処理 (1)
施設の場所の問題 (1)
ポートフォリオの最適化 (1)
リスクが最小でリターンが最大になるような,資本 ![]() の6つの株式への投資配分を求める:
の6つの株式への投資配分を求める:
リターンは ![]() で与えられる.ただし,
で与えられる.ただし,![]() は個別の株式の予想収益の値のベクトルである:
は個別の株式の予想収益の値のベクトルである:
リスクは ![]() で与えられる.
で与えられる.![]() はリスク回避パラメータであり,
はリスク回避パラメータであり,![]() である:
である:
目的は,指定されたリスク回避パラメータについてリスクを最小にしつつリターンを最大にすることである:
重み ![]() はどれも0より大きくなければならず,重みに市場影響コストを加えたものは1でなければならない:
はどれも0より大きくなければならず,重みに市場影響コストを加えたものは1でなければならない:
リスク回避パラメータの範囲について,利益と対応するリスクを計算する:
範囲 ![]() での最適な
での最適な ![]() は,リスクとリターンのトレードオフの上界包絡線を与える:
は,リスクとリターンのトレードオフの上界包絡線を与える:
市場コストを説明することで,低リスク回避のための多様化したポートフォリオが得られるが,リスク回避が高い場合は,多様化されていない株式を購入するため,市場への影響コストが支配的になる:
軌道最適化 (1)
製造問題 (3)
指定された歯車比を生成するために,ギア ![]() に必要な歯車
に必要な歯車 ![]() の数を求める:
の数を求める:
圧力釜の製造コストを最小にする.釜は長さ ![]() ,半径
,半径 ![]() の円柱形シェルで,円柱の両端に半球のキャップが付いている:
の円柱形シェルで,円柱の両端に半球のキャップが付いている:
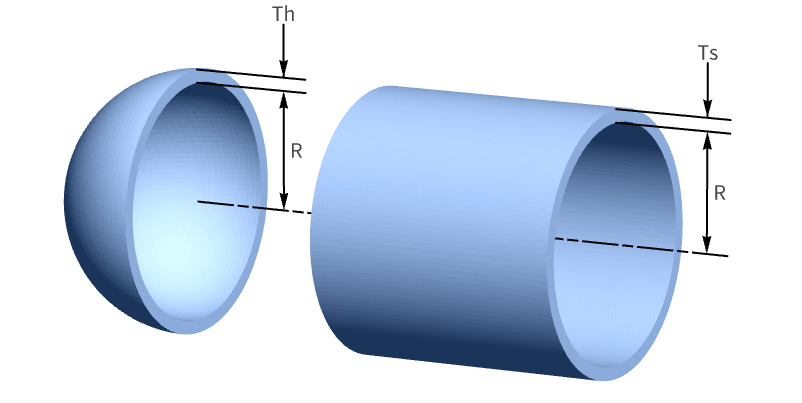
シェルの厚さは ![]() で半球キャップの厚さは
で半球キャップの厚さは ![]() である.シェルとキャップの厚さには上限と下限が指定されており,半径との比よりも大きくなければならない:
である.シェルとキャップの厚さには上限と下限が指定されており,半径との比よりも大きくなければならない:
シェルとキャップの材料の密度は ![]() である.材料コストは以下の通りである:
である.材料コストは以下の通りである:
軸荷重をに依存する,巻き径 ![]() ,線バネ径
,線バネ径![]() ,バネコイル
,バネコイル ![]() の最小体積の圧縮コイルバネを設計する:
の最小体積の圧縮コイルバネを設計する:
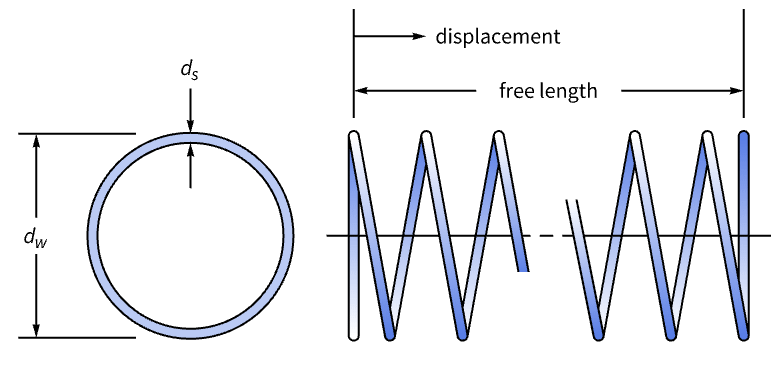
バネにかかる剪断応力は,最大許容軸荷重 ![]() に依存し,最大許容応力
に依存し,最大許容応力 ![]() より低くなければならない:
より低くなければならない:
巻き径 ![]() は,バネコイルがキツく巻かれすぎないようにするために,少なくとも線バネ径
は,バネコイルがキツく巻かれすぎないようにするために,少なくとも線バネ径 ![]() の3倍でなければならない.
の3倍でなければならない.
たわみと事前荷重によって生じる荷重 ![]() は,最大荷重
は,最大荷重 ![]() を超えてはならない:
を超えてはならない:
バネコイルはミュージックワイヤー スプリング鋼ASTM A228から製造され,ワイヤーの直径は一連の所定の直径から選択する必要がある:
特性と関係 (9)
NMinimizeは最小値と,変数の値を最小にする規則を与える:
NArgMinは最小化する値のリストを与える:
NMinValueは最小値だけを与える:
凸問題については,ConvexOptimizationを使って追加的な解の特性が得られるかもしれない:
パラメータがある凸問題についてParametricConvexOptimizationを使うとParametricFunctionが与えられる:
ParametricFunctionはパラメータの値について評価できる:
NMinimizeを使ってパラメトリック問題についての関数を定義する:
ParametricFunctionの導関数も計算できる:
RobustConvexOptimizationは,パラメータ制約がある凸問題についてはパラメータの可能なすべての値について有効な最適値を求める:
NMinimizeはパラメータの特定の値についてより小さい値を求めるかもしれない:
このミニマイザは α と β の使用可能なすべての値についての制約条件は満足しない:
パラメータの特定の値について求まった最小値はロバストな最小値以下である:
NMinimizeは大域的である最小値を求めようとするのに対し,FindMinimumは極小値(局所的な最小値)を求めようとする:
FindFitはNMinimizeを使って大域的最適フィットを求めることができる.次でそのモデルを設定する:
デフォルトで,FindFitは局所的最適フィットしか求めない:
NMinimizeメソッドを使うと大域的最適フィットが求まる:
RegionDistanceとRegionNearestを使って距離と最近点を計算する:
どちらもNMinimizeを使って計算することができる:
RegionBoundsを使って境界ボックスを計算する:
考えられる問題 (3)
非線形の関数の場合は,NMinimizeは,メソッドによっては極小値しか見付けられないことがある:
NMinimizeは,メソッドによっては円板上で二次元関数の極小値を求める:
この関数を記号パラメータに適用するとNIntegrateからメッセージが生成される:
この関数をNMinimizeのような他の数値関数と一緒に使っても同じように警告が出る:
メッセージが出るのを避けるために,引数が数値のときにだけ評価する関数を定義する:
これで,この関数をNMinimizeのような他の数値関数と一緒に使えるようになった:
テキスト
Wolfram Research (2003), NMinimize, Wolfram言語関数, https://reference.wolfram.com/language/ref/NMinimize.html (2024年に更新).
CMS
Wolfram Language. 2003. "NMinimize." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/NMinimize.html.
APA
Wolfram Language. (2003). NMinimize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NMinimize.html