NestGraph
NestGraph
詳細とオプション
- NestGraphは，Crawlグラフあるいは木の成長としても知られている．
- expr は，式または式のリスト，あるいはグラフでよい．
- NestGraph[f,expr]はNestGraph[f,expr,1]に等しい．
- NestGraph[f,expr]は辺が{exprexpr1,…,exprexprk}のグラフを与える．f[expr]を評価すると{expr1,…,exprk}になる．
- NestGraph[f,{expr1,expr2,…}]はNestGraph[f,expr1]とNestGraph[f,expr2],…のグラフ和集合を与える．
- NestGraph[f,graph]は，graph とNestGraph[f,{v1,…}]の和集合である．viは graph の頂点である．
- NestGraph[f,graph,n]は NestGraph[f,graph,n-1]とNestGraph[f,{v1,…}]の和集合である．viは NestGraph[f,graph,n-1]の頂点である．
- NestGraph[f,expr,n]はNestGraph[f,graph,n]に等しい．graph は唯一の頂点 expr を持ち辺はないシングルトングラフである．
- NestGraphはGraphと同じオプションを取る．
- オプションDirectedEdgesを使って有向グラフと無向グラフのどちらを構築するかを制御することができる．
全オプションのリスト
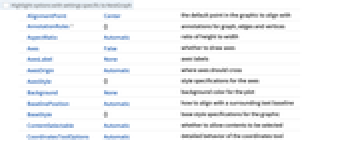
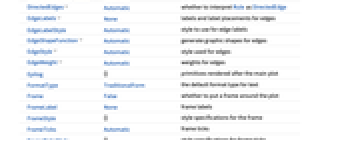
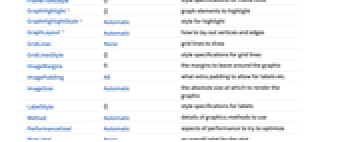
例題
すべて開く すべて閉じる例 (4)
x から始め，f を連続的に3回適用することでグラフを構築する：
NestGraph[f, x, 3, VertexLabels -> Automatic, ImagePadding -> 40]NestGraph[Mod[# ^ 2 + 1, 10]&, Range[0, 9], VertexLabels -> Automatic]NestGraph[{f[#], g[#]}&, x, 3, VertexLabels -> Automatic]NestGraph[#["BorderingCountries"]&, ["switzerland"], 2, VertexLabels -> Automatic]スコープ (3)
NestGraphは式を含む任意の関数に使うことができる：
NestGraph[f, x, 3]NestGraph[Mod[# ^ 2 + 1, 10]&, Range[0, 9], 2]NestGraphは，整数を含む任意の式に使うことができる：
NestGraph[Mod[# ^ 2 + 1, 10]&, {1, 2, 3, 4, 5}, 2]NestGraph[WordData[#, "Synonyms", "List"] &, "tree", 2]NestGraph[WordData[#, "Synonyms", "List"] &, [image], 2]NestGraph[WordData[#, "Synonyms", "List"] &, "tree", 3]オプション (80)
AnnotationRules (2)
DirectedEdges (1)
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 4], 2]DirectedEdges->Falseを使って無向グラフを生成する：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 4], 2, DirectedEdges -> False]EdgeLabels (7)
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> {12 -> "Hello"}]el = EdgeList[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2]]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], EdgeLabels -> Table[el[[i]] -> Subscript["e", i], {i, Length[el]}]]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> {01 -> [image], 12 -> [image], 20 -> [image]}]Placedを記号的な位置と一緒に使って辺に沿ったラベルの置き方を制御する：
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> {12 -> Placed["■■■", p]}, PlotLabel -> p], {p, {"Start", "Middle", "End"}}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> {12 -> Placed["■■■", p]}, PlotLabel -> p, BaselinePosition -> Bottom], {p, {0, 1 / 4, 1 / 3}}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> {12 -> Placed["■■■", {1 / 2, p}]}, PlotLabel -> p, BaselinePosition -> Bottom], {p, {{0, 0}, {1 / 2, 1 / 2}, {1, 1}}}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> {12 -> Placed[{"lbl1", "lbl2"}, {"Start", "End"}]}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> {12 -> Placed[{"lbl1", "lbl2", "lbl3"}, {"Start", "Middle", "End"}]}]TooltipとStatusAreaからの値によって自動ラベル付けを行う：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> Placed["Name", Tooltip]]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeLabels -> Placed["Name", StatusArea]]EdgeShapeFunction (6)
EdgeShapeFunctionについての組込み設定のリストを得る：
ResourceData["EdgeShapeFunction"]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeShapeFunction -> "Line"]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeShapeFunction -> {{ef, "ArrowSize" -> 0.1}}, PlotLabel -> ef], {ef, {"BoxLine", "DiamondLine", "DotLine"}}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeShapeFunction -> {{ef, "ArrowSize" -> 0.1}}, PlotLabel -> ef], {ef, ResourceData["EdgeShapeFunction", "FilledArrow"]}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeShapeFunction -> {{ef, "ArrowSize" -> 0.1}}, PlotLabel -> ef], {ef, ResourceData["EdgeShapeFunction", "UnfilledArrow"]}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeShapeFunction -> {{ef, "ArrowSize" -> 0.1}}, PlotLabel -> ef], {ef, ResourceData["EdgeShapeFunction", "CarvedArrow"]}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeShapeFunction -> {12 -> "DotLine"}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeShapeFunction -> {12 -> "BoxLine", "DotLine"}]ef[pts_List, e_] :=
Block[{s = 0.015, g = [image]}, {Arrowheads[{{s, 0.33, g}, {s, 0.67, g}}], Arrow[pts]}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeShapeFunction -> ef]EdgeShapeFunctionはEdgeStyleと組み合せることができる：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeStyle -> Blue, EdgeShapeFunction -> (Line[#1]&)]EdgeShapeFunctionはEdgeStyleより優先順位が高い：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeStyle -> Blue, EdgeShapeFunction -> ({Red, Line[#1]}&)]EdgeStyle (2)
EdgeWeight (2)
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeWeight -> RandomInteger[5, 3]]WeightedAdjacencyMatrix[%]//MatrixFormNestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, EdgeWeight -> {a, b, c}]WeightedAdjacencyMatrix[%]//MatrixFormGraphHighlight (3)
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> Tiny, GraphHighlight -> {1}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> Tiny, GraphHighlight -> {12}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> Tiny, GraphHighlight -> {1, 2, 01, 12}]GraphHighlightStyle (2)
GraphHighlightStyleについての組込み設定のリストを得る：
ResourceData["GraphHighlightStyle"]GraphHighlightStyleについての組込み設定を使う：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, GraphHighlight -> {1, 12}, VertexSize -> Small, GraphHighlightStyle -> #, PlotLabel -> #]& /@ Select[ResourceData["GraphHighlightStyle"], # =!= Automatic&]GraphLayout (5)
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 10], 2, GraphLayout -> Automatic]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 10], 2, GraphLayout -> l, PlotLabel -> l], {l, {"CircularEmbedding", "SpiralEmbedding"}}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 20], 2, GraphLayout -> l, PlotLabel -> l], {l, {"SpringEmbedding", "SpringElectricalEmbedding", "HighDimensionalEmbedding"}}]VertexCoordinatesはGraphLayout座標を上書きする：
{NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 5], 2, GraphLayout -> "SpringElectricalEmbedding"],
WheelGraph[5, GraphLayout -> "SpringElectricalEmbedding", VertexCoordinates -> Table[{i, i}, {i, 0, 4}]]}AbsoluteOptionsによってレイアウトアルゴリズムを使って計算されたVertexCoordinatesを抽出する：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 5], 2]AbsoluteOptions[%, VertexCoordinates]PlotTheme (4)
基本テーマ (2)
VertexCoordinates (3)
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2]AbsoluteOptionsを使って結果の頂点座標を抽出する：
AbsoluteOptions[%, VertexCoordinates]ellipseLayout[n_, {a_, b_}] := Table[{a Cos[2Pi / n u], b Sin[2Pi / n u]}, {u, 1, n}]Graphics[Point[ellipseLayout[20, {2, 1}]]]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 19], 2, VertexCoordinates -> ellipseLayout[20, {2, 1}]]VertexCoordinatesはGraphLayoutより優先順位が高い：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 3], 2, VertexCoordinates -> Table[{i, i}, {i, 4}], GraphLayout -> "CircularEmbedding"]VertexLabels (13)
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> "Name"]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> {2 -> "one"}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> Table[i -> Subscript[v, i], {i, 0, 2}]]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> {1 -> [image], 2 -> [image], 0 -> [image]}, ImagePadding -> 20]Placedを記号的な位置と一緒に使って，外側位置を含むラベルの置き方を制御する：
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.1, VertexShapeFunction -> "Square", VertexLabels -> Table[i -> Placed["■■■", p], {i, 0, 2}], PlotLabel -> p, ImagePadding -> 20], {p, {Before, After, Below, Above}}]pl = {{Before, Below}, {After, Below}, {Before, Above}, {After, Above}};Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.1, VertexShapeFunction -> "Square", ImagePadding -> 20, VertexLabels -> Table[i -> Placed["■■■", p], {i, 0, 2}], PlotLabel -> p], {p, pl}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.45, VertexLabels -> Table[i -> Placed["■■■", p], {i, 0, 2}], VertexShapeFunction -> "Square", PlotLabel -> p], {p, {Left, Top, Right, Bottom}}]pl = {{Left, Bottom}, {Right, Bottom}, {Left, Top}, {Right, Top}};Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.45, VertexShapeFunction -> "Square", VertexLabels -> Table[i -> Placed["■■■", p], {i, 0, 2}], PlotLabel -> p], {p, pl}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.25, VertexShapeFunction -> "Square", VertexLabels -> Table[i -> Placed[[image], p], {i, 0, 2}], PlotLabel -> p, BaselinePosition -> Bottom], {p, {{0, 0}, {1 / 2, 1 / 2}, {1, 1}}}]すべてのラベルを頂点の右上コーナーに置き，ラベル内の座標を変える：
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.35, VertexShapeFunction -> "Square", VertexLabels -> Table[i -> Placed[[image], {{1, 1}, p}], {i, 0, 2}], PlotLabel -> p, BaselinePosition -> Bottom], {p, {{0, 0}, {1 / 2, 1 / 2}, {1, 1}}}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> {1 -> Placed[{"lbl1", "lbl2"}, {Above, Below}]}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> {1 -> Placed[{"lbl1", "lbl2", "lbl3", "lbl4"}, {Above, After, Below, Before}]}]日木津雨Placedを使ってTooltipを含むフォーマットを制御する：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> Placed["Name", Tooltip]]あるいはStatusAreaを使って：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> Placed["Name", StatusArea]]rotateLabel[lbl_] := Rotate[lbl, 45Degree]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> Table[i -> Placed["xxx", Below, rotateLabel], {i, 0, 2}]]panelLabel[lbl_] := Panel[lbl, FrameMargins -> 0, Background -> StandardYellow]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> Table[i -> Placed["xxx", Center, panelLabel], {i, 0, 2}]]hyperlinkLabel[lbl_] := Hyperlink[lbl, "http://www.wolfram.com"]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexLabels -> Table[i -> Placed["xxx", Center, hyperlinkLabel], {i, 0, 2}]]VertexShape (5)
任意のGraphics，ImageあるいはGraphics3Dを頂点の形として使う：
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShape -> s, VertexSize -> Medium], {s, {[image], [image], [image]}}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShape -> {2 -> [image]}, VertexSize -> Medium]VertexShapeはVertexSizeと組み合せることができる：
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> s, VertexShape -> [image], PlotLabel -> s], {s, {Small, Large}}]VertexShapeはVertexStyleの影響を受けない：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.2, VertexShape -> [image], VertexStyle -> Blue]VertexShapeFunctionはVertexShapeより優先順位が高い：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.2, VertexShapeFunction -> "Square", VertexShape -> [image]]VertexShapeFunction (10)
VertexShapeFunctionの組込みコレクションのリストを得る：
ResourceData["VertexShapeFunction"]"Basic"コレクション中のVertexShapeFunctionの組込み設定を使う：
ResourceData["VertexShapeFunction", "Basic"]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> vf, VertexSize -> 0.2, PlotLabel -> vf], {vf, {"Triangle", "Square", "Rectangle", "Pentagon", "Hexagon", "Octagon"}}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> vf, VertexSize -> 0.2, PlotLabel -> vf], {vf, {"DownTrapezoid", "UpTrapezoid", "Parallelogram", "FiveDown", "Circle", "Diamond", "Star", "Capsule"}}]"Rounded"コレクション中のVertexShapeFunctionの組込み設定を使う：
ResourceData["VertexShapeFunction", "Rounded"]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> vf, VertexSize -> 0.2, PlotLabel -> vf], {vf, ResourceData["VertexShapeFunction", "Rounded"]}]"Concave"コレクション中のVertexShapeFunctionの組込み設定を使う：
ResourceData["VertexShapeFunction", "Concave"]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> vf, VertexSize -> 0.2, PlotLabel -> vf], {vf, ResourceData["VertexShapeFunction", "Concave"]}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> { 1 -> "Square"}, VertexSize -> 0.2]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> { 1 -> "Square", "Triangle"}, VertexSize -> 0.2]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> (Inset[[image], #]&)]vf[{xc_, yc_}, name_, {w_, h_}] :=
Block[{xmin = xc - w, xmax = xc + w, ymin = yc - h, ymax = yc + h},
Polygon[{{xmin, ymin}, {xmax, ymax}, {xmin, ymax}, {xmax, ymin}}]
];NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> vf, VertexSize -> 0.2]VertexShapeFunctionはVertexStyleと組み合せることができる：
vf1[{xc_, yc_}, name_, {w_, h_}] := Rectangle[{xc - w, yc - h}, {xc + w, yc + h}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.2, VertexStyle -> Blue, VertexShapeFunction -> vf1]VertexShapeFunctionはVertexStyleより優先順位が高い：
vf2[{xc_, yc_}, name_, {w_, h_}] := {Red, Rectangle[{xc - w, yc - h}, {xc + w, yc + h}]}NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.2, VertexStyle -> Blue, VertexShapeFunction -> vf2]VertexShapeFunctionはVertexSizeより優先順位が高い：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexShapeFunction -> "Star", VertexSize -> {1 -> Small, Medium}]VertexShapeFunctionはVertexShapeより優先順位が高い：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.3, VertexShapeFunction -> "Star", VertexShape -> [image]]VertexSize (8)
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> Automatic]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> s, PlotLabel -> s], {s, {Tiny, Small, Medium, Large}}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> s, PlotLabel -> s], {s, 0.1, 1, 0.3}]Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> {"Scaled", s}, PlotLabel -> {"Scaled", s}], {s, 0.1, 1, 0.3}]
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> s, PlotLabel -> s], {s, {{0.1, 0.2}, {0.2, 0.1}}}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> {1 -> 0.2, 2 -> 0.3}]VertexSizeはVertexShapeFunctionと組み合せることができる：
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> s, VertexShapeFunction -> "Square", PlotLabel -> s], {s, {0.05, 0.1, 0.2}}]VertexSizeはVertexShapeと組み合せることができる：
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> s, VertexShape -> [image], PlotLabel -> s], {s, {0.1, 0.2, 0.4}}]VertexStyle (5)
Table[NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexStyle -> style, VertexSize -> 0.3, PlotLabel -> style], {style, {Yellow, EdgeForm[Dashed]}}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexStyle -> {1 -> Blue, 2 -> Red}, VertexSize -> 0.2]VertexShapeFunctionはVertexStyleと組み合せることができる：
vf1[{xc_, yc_}, name_, {w_, h_}] := Rectangle[{xc - w, yc - h}, {xc + w, yc + h}]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.2, VertexStyle -> Blue, VertexShapeFunction -> vf1]VertexShapeFunctionはVertexStyleより優先順位が高い：
vf2[{xc_, yc_}, name_, {w_, h_}] := {Red, Rectangle[{xc - w, yc - h}, {xc + w, yc + h}]}NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.2, VertexStyle -> Blue, VertexShapeFunction -> vf2]VertexStyleはBaseStyleと組み合せることができる：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexStyle -> LightBlue, BaseStyle -> EdgeForm[Dotted], VertexSize -> 0.2]VertexStyleはBaseStyleより優先順位が高い：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexStyle -> LightBlue, BaseStyle -> Gray, VertexSize -> 0.2]VertexShapeはVertexStyleの影響は受けない：
NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexSize -> 0.2, VertexShape -> [image], VertexStyle -> Blue]VertexWeight (2)
WheelGraph[4, VertexWeight -> {2, 3, 4, 5}]AnnotationValue[{%, 1}, VertexWeight]NestGraph[Mod[# ^ 2 + 1, 5]&, Range[0, 2], 2, VertexWeight -> {a, b, c}]AnnotationValue[{%, 1}, VertexWeight]アプリケーション (2)
Wolfram言語中の「近隣」関数のネットワークを生成する：
NestGraph[WolframLanguageData[#, EntityProperty["WolframLanguageSymbol", "RelatedSymbols"]]&, Entity["WolframLanguageSymbol", "Nest"], 2, VertexLabels -> "Name"]NestGraph[FileNames["*", #] &, $InstallationDirectory, 3, VertexLabels -> Placed["Name", Tooltip]]特性と関係 (5)
VertexCountとEdgeCountを使って頂点と辺を数える：
g = NestGraph[Mod[# ^ 2 + 1, 10]&, {1, 2, 3, 4, 5}, 2]{VertexCount[g], EdgeCount[g]}VertexListとEdgeListを使って頂点と辺を標準的な順序で列挙する：
g = NestGraph[WordData[#, "Synonyms", "List"] &, "tree", 2]{VertexList[g], EdgeList[g]}グラフからAdjacencyMatrixを計算する：
g = NestGraph[f, x, 3];AdjacencyMatrix[g]//MatrixFormNeighborhoodGraphはNestGraphを使って求めることができる：
g = GridGraph[{4, 4}];g1 = NeighborhoodGraph[g, 1, 2]g2 = NestGraph[Rest@VertexOutComponent[g, #, 1]&, 1, 2, DirectedEdges -> False]//SimpleGraphIsomorphicGraphQ[g1, g2]NestList[{f[#], g[#]}&, x, 3]NestGraph[{f[#], g[#]}&, x, 3, VertexLabels -> "Name"]おもしろい例題 (1)
「math」で始まる長さ等しい最も近くの単語を表示するネストしたグラフを作成する：
word = "math";words = Select[WordList[], StringLength[#] == StringLength[word]&];SmallestEditDistances[word_] := Nearest[Complement[words, {word}], word]HighlightGraph[NestGraph[SmallestEditDistances, word, 2, VertexLabels -> All], word]
An Elementary Introduction to the Wolfram Language
Wolfram Research (2015), NestGraph, Wolfram言語関数， https://reference.wolfram.com/language/ref/NestGraph.html.
テキスト
Wolfram Research (2015), NestGraph, Wolfram言語関数， https://reference.wolfram.com/language/ref/NestGraph.html.
CMS
Wolfram Language. 2015. "NestGraph." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NestGraph.html.
APA
Wolfram Language. (2015). NestGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NestGraph.html