NoncentralBetaDistribution
NoncentralBetaDistribution[α,β,δ]
表示形状参数为 α 与 β、非中心参数为 δ 的非中心 β 分布.
更多信息
- 在非中心 β 分布中,当
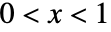 时,值
时,值 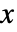 的概率密度与
的概率密度与 ![x^(alpha-1)(1-x)^(beta-1) TemplateBox[{{alpha, +, beta}, alpha, {{(, {x, , delta}, )}, /, 2}}, Hypergeometric1F1] x^(alpha-1)(1-x)^(beta-1) TemplateBox[{{alpha, +, beta}, alpha, {{(, {x, , delta}, )}, /, 2}}, Hypergeometric1F1]](Files/NoncentralBetaDistribution.zh/3.png) 成正比,当
成正比,当 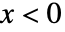 或
或 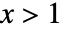 时为零.
时为零. - NoncentralBetaDistribution 允许 α、β 和 δ 为任意正实数.
- NoncentralBetaDistribution 允许 α、β 和 δ 为无量纲量.
- NoncentralBetaDistribution 可与 Mean、CDF 以及 RandomVariate 等函数联合使用.
背景
- NoncentralBetaDistribution[α,β,δ] 表示定义在区间
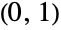 上的连续统计分布,由正实数 α、β 和 δ(分别是两个“形状参数”和一个"非中心化参数")作为参数,共同决定其概率密度函数(PDF)的整体行为. NoncentralBetaDistribution 是 BetaDistribution (有时称作中心化贝塔分布)或许倾斜的推广,尽管它最常被称为非中心贝塔分布,也存在一些其它贝塔分布的非中心推广.
上的连续统计分布,由正实数 α、β 和 δ(分别是两个“形状参数”和一个"非中心化参数")作为参数,共同决定其概率密度函数(PDF)的整体行为. NoncentralBetaDistribution 是 BetaDistribution (有时称作中心化贝塔分布)或许倾斜的推广,尽管它最常被称为非中心贝塔分布,也存在一些其它贝塔分布的非中心推广. - NoncentralBetaDistribution 是比值
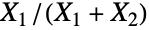 的分布,其中
的分布,其中 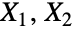 中恰好有一个是非中心卡方(NoncentralChiSquareDistribution)随机变元. 因此,它与 BetaDistribution 类似,后者模拟的是卡方(ChiSquareDistribution)随机变元
中恰好有一个是非中心卡方(NoncentralChiSquareDistribution)随机变元. 因此,它与 BetaDistribution 类似,后者模拟的是卡方(ChiSquareDistribution)随机变元 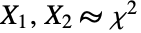 的比值
的比值 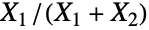 . 尽管该分布在20 世纪 20 年代就被推导出来,但它的详细属性直到20 世纪 50 年代才由统计学家J. L. Hodges首次研究. 自那时起,该分布被用于模拟各种现象,包括信号分析中的信号对之间的一致性,以及金融领域的资产交换收益等.
. 尽管该分布在20 世纪 20 年代就被推导出来,但它的详细属性直到20 世纪 50 年代才由统计学家J. L. Hodges首次研究. 自那时起,该分布被用于模拟各种现象,包括信号分析中的信号对之间的一致性,以及金融领域的资产交换收益等. - RandomVariate 可用于给出一个或多个机器精度或任意精度(后者通过 WorkingPrecision 选项)的非中心贝塔分布的伪随机变元. Distributed[x,NoncentralBetaDistribution[α,β,δ]],更简洁的表示为xNoncentralBetaDistribution[α,β,δ],可用于声明随机变量 x 服从非中心贝塔分布. 然后这类声明可用于诸如 Probability、NProbability、Expectation 和 NExpectation 等函数中.
- 非中心贝塔分布的概率密度和累积分布函数可以通过使用PDF[NoncentralBetaDistribution[α,β,δ],x] 和CDF[NoncentralBetaDistribution[α,β,δ],x] 给出. 均值、中位数、方差、原始矩和中心矩可以分别使用 Mean、Median、Variance、Moment 和 CentralMoment 计算.
- DistributionFitTest 可用于检验给定的数据集是否与非中心贝塔分布相一致,EstimatedDistribution 可用于通过给定数据估计非中心贝塔参数分布,而FindDistributionParameters 可用于将数据拟合为非中心贝塔分布. ProbabilityPlot 可用于生成已知数据相对于符号式非中心贝塔分布的 CDF 图形,而QuantilePlot 可用于生成已知数据相对于符号式非中心贝塔分布的分位数的分位数图形.
- TransformedDistribution 可用于表示非中心贝塔分布的变换,CensoredDistribution 可用于表示在上限和下限值之间删失值的分布,TruncatedDistribution 可用于表示在上限和下限值之间截断值的分布. CopulaDistribution 可用于构建包含非中心贝塔分布的更高维分布,而 ProductDistribution 可用于计算独立分量分布涉及非中心贝塔分布的联合分布.
- NoncentralBetaDistribution 与若干其他统计分布相关. NoncentralBetaDistribution[α,β,δ] 的 PDF 在 δ→0 时趋向于BetaDistribution[α,β] 的 PDF,在这种意义上,它是 BetaDistribution 的直接推广 . NoncentralBetaDistribution 可以通过 NoncentralFRatioDistribution 和 NoncentralChiSquareDistribution 的变换得到,也与 PERTDistribution、PearsonDistribution、ChiSquareDistribution、GammaDistribution、FRatioDistribution 和 BetaPrimeDistribution 密切相关.
范例
打开所有单元关闭所有单元范围 (6)
属性和关系 (4)
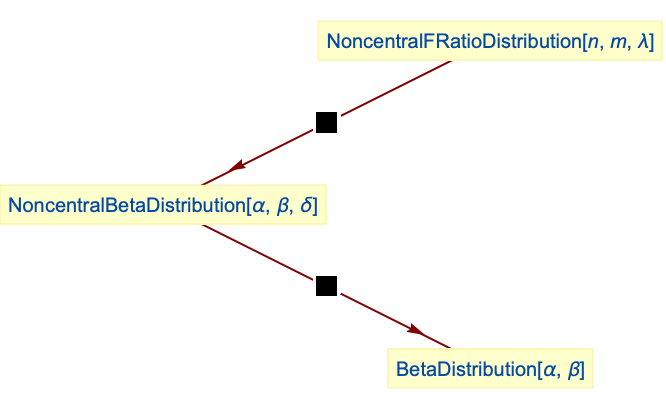
当非中心参数 δ 变为 0 时,这是 BetaDistribution:
NoncentralBetaDistribution 是 NoncentralFRatioDistribution 的一个变换:
NoncentralBetaDistribution 可以作为 ChiSquareDistribution 和NoncentralChiSquareDistribution 的一个变换得到:
Wolfram Research (2010),NoncentralBetaDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html (更新于 2016 年).
文本
Wolfram Research (2010),NoncentralBetaDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2010. "NoncentralBetaDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html.
APA
Wolfram 语言. (2010). NoncentralBetaDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html 年