Quantile

Quantile[data,p]

给出估计的 data 的第 p 分位数 .

Quantile[data,{p1,p2,…}]

给出分位数列表 p1,p2,….

Quantile[data,p,{{a,b},{c,d}}]

使用参数 a、b、c、d 指定的分位数定义.

Quantile[dist,p]

给出分布 dist 的分位数.

更多信息

  • Quantile 亦称为风险值 (VaR) 或分位值.
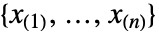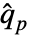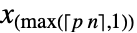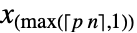  • 当 VectorQ data 被排序为 时，分位数估计值 由 给出.
  • 对于 MatrixQ data，针对每个列向量计算分位数，Quantile[{{x1,y1,…},{x2,y2,…},…},p] 等价于 {Quantile[{x1,x2,…},p],Quantile[{y1,y2,…},p]}. »
  • 对于 ArrayQ data，分位数等价于 ArrayReduce[Quantile,data,1]. »
  • Quantile[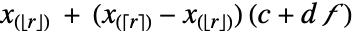{x_1,...,x_n},p,{{a,b},{c,d}}] 由 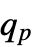给出， r=a+(n+b)p，⌊r⌋= Floor[r]，⌈r⌉=Ceiling[r] 和 =FractionalPart[r]. 如果索引超出范围，将其视为 1 或 n. »
  • 参数 {{a,b},{c,d}} 的常见选择包括：
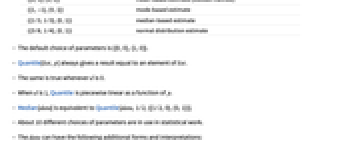
  • {{0,0},{1,0}}逆经验 CDF（默认）
    {{0,0},{0,1}}线性插值（California 法）
    {{1/2,0},{0,0}}编号最接近 p n 的元素
    {{1/2,0},{0,1}}线性插值（水文学法）
    {{0,1},{0,1}}基于均值的估计（Weibull 法）
    {{1,-1},{0,1}}基于众数的估计
    {{1/3,1/3},{0,1}}基于中位数的估计
    {{3/8,1/4},{0,1}}正态分布估计
  • 参数的默认选择为 {{0,0},{1,0}}.
  • 统计工作中使用了大约 10 种不同的参数选择.
  • Quantile[list,p] 总是给出等于 list 的一个元素的结果.
  • d 为 0 时同样成立.
  • d 为 1 时，Quantile 是 p 的分段线性函数.
  • Median[data] 等价于 Quantile[data,1/2,{{1/2,0},{0,1}}].
  • data 可以有以下其他形式和解释：
  • Association数值（键被忽略） »
    SparseArray数组，相当于 Normal[data] »
    QuantityArray量组成的数组 »
    WeightedData基于 EmpiricalDistribution »
    EventData基于 SurvivalDistribution »
    TimeSeries, TemporalData, …向量或数值组成的数组（忽略时间戳） »
    Image,Image3DRGB 通道的值或灰度的强度值 »
    Audio所有通道的幅值 »
    DateObject, TimeObject日期列表或时间列表 »
  • Quantile[dist,p] 等价于 InverseCDF[dist,p].
  • Quantile[dist,p] 是一组数字 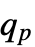q_(p) 的最小值，使得 Probability[x≤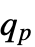q_(p),xdist]≥p 和 Probability[x≥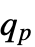q_(p),xdist]≥p. »
  • 对于随机过程 proc，可计算时间 t 处切片分布 SliceDistribution[proc,t] 的分位数函数，即 Quantile[SliceDistribution[proc,t], p]. »
  • 值 p 可以是符号和任意位于 0 和 1 之间的数字. »

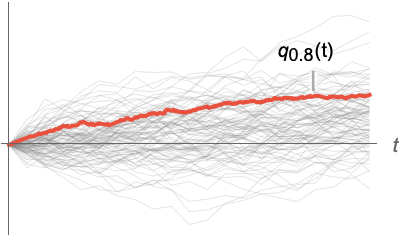
范例

打开所有单元关闭所有单元

基本范例  (7)

找出一个列表中的中间值：

求列表的 20% 和 80% 分位数：

列表的最高分位数：

日期列表的分位数：

正态分布的 q 分位数：

连续单元分布的分位数函数：

离散单元分布的分位数函数：

范围  (33)

基本用法  (7)

Quantile 适用于任何实数：

获取任意精度的结果：

用其他参数化计算结果：

求 WeightedData 的分位数：

求 EventData 的分位数：

求 TimeSeries 的分位数：

分位数只取决于值：

求含有量的数据的分位数：

数组数据  (6)

求每一列元素的分位数：

求每一列元素的多个分位数：

张量的分位数给出第一级的列的分位数：

计算大型向量或矩阵的分位数：

当输入为 Association 时，Quantile 只作用于值：

计算 SparseArray 的分位数：

求 QuantityArray 的分位数：

图像和音频数据  (2)

按通道计算的 RGB 图像的 30% 分位数：

灰度图的强度值的 30% 分位数：

所有通道的幅值的 30% 分位数：

日期和时间  (5)

计算日期的分位数：

计算日期的加权分位数：

计算以不同的日历给出的日期的分位数：

以输入的一种日历格式给出分位数：

计算时间的分位数：

计算以不同的时区规范给出的时间的分位数：

参数分布  (5)

获得确切的数值解：

获得机器精度的结果：

获得连续分布任何精度的结果：

获得分位数的符号表达式：

Quantile 依次作用于列表的每个元素：

非参数分布  (2)

非参数分布的 Quantile：

与底层参数分布比较值：

为直方图分布绘制分位数：

导出分布  (4)

截断分布的 Quantile：

指数分布的二次变换：

删截分布：

含有量的分布的分位数：

随机过程  (2)

随机过程的四分位函数：

求某些时间 t=0.5 处，TemporalData 的四分位数：

求所有的模拟和相应的四分位函数：

应用  (7)

间隔均匀的 个分位数组将数值划分为 个尺寸相同的组：

计算一组分位数：

根据分位数的数值将概率密度函数绘制为5个区：

将分位数作为网格函数使用：

绘制列表的第 q 分位数的曲线：

绘制线性内插分位数的曲线：

使用四分位数 计算期望值:

在 Expectation 中使用该方法:

通过非均匀分布的分位数函数转化均匀分布，生成非均匀分布的随机数：

比较样本的直方图和期待分布的概率密度函数：

计算某些数据的平移四分位数：

使用长度为 .1 的窗：

计算随机过程路径集合切片的选择分位数：

选择一些切片时间：

在这些路径上绘制分位数图线：

计算一个班级孩子们的身高的分位数：

属性和关系  (9)

使用 Quantile 求解分布的分位数：

直接计算分位数：

在默认参数下，Quantile 总是返回列表框中的一个元素：

Quartiles 给出列表的线性内插 Quantile 值：

InterquartileRange 是列表的线性内插 Quantile 值的差值：

QuartileDeviation 是列表的线性内插 Quantile 值的差值的一半：

QuartileSkewness 把线性内插 Quantile 值法作为偏差量的测量方法：

Quantile 对于分布数来说和 InverseCDF 等效：

QuantilePlot 绘制列表或者分布的四分位数图线：

BoxWhiskerChart 显示数据的特定四分位数：

可能存在的问题  (4)

如果对数据进行计算，p 可以是 0 到 1 之间的任意数字：

对于某些分布，可能存在符号解析式：

对于某些分布不存在符号闭合形式：

但可以进行数值计算：

把无效的值带入符号输出，得出的结果没有意义：

作为参数代入，则不进行计算：

通过 Quantile 计算的数据的四分位数与通过 Quartiles 计算的结果并不总是一致：

直接计算分位数：

指定 Quantile 中的线性插值参数：

巧妙范例  (1)

在 20、100 和 300 个样本时的 Quantile 估计值分布：

Wolfram Research (2003)，Quantile，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Quantile.html （更新于 2024 年）.

文本

Wolfram Research (2003)，Quantile，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Quantile.html （更新于 2024 年）.

CMS

Wolfram 语言. 2003. "Quantile." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Quantile.html.

APA

Wolfram 语言. (2003). Quantile. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Quantile.html 年

BibTeX

@misc{reference.wolfram_2024_quantile, author="Wolfram Research", title="{Quantile}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Quantile.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_quantile, organization={Wolfram Research}, title={Quantile}, year={2024}, url={https://reference.wolfram.com/language/ref/Quantile.html}, note=[Accessed: 21-November-2024 ]}