RandomGraph

RandomGraph[{n,m}]

n 個の頂点と m 本の辺を持つ擬似ランダムグラフを返す．

RandomGraph[{n,m},k]

k 個の擬似ランダムグラフのリストを返す．

RandomGraph[gdist,…]

ランダムグラフ分布 gdist からのサンプルを返す．

詳細とオプション

RandomGraph[{n,m}]はRandomGraph[UniformGraphDistribution[n,m]]に等しい．
RandomGraphは，Wolfram言語を実行するたびに擬似ランダムグラフの異なる数列を返す．SeedRandomを使うと繰返し可能な数列が得られる．
頂点は整数 1, …, n であるとみなされる．
SeedRandomのメソッドオプションで，使用する擬似乱数ジェネレータが指定できる．
RandomGraph[dist,{n₁,n₂,…}]はグラフの n₁×n₂×…配列を返す．
RandomGraphにはGraphと同じオプションが使える．

全オプションのリスト

AlignmentPoint	Center	整列の基準となるグラフィックス内のデフォルトの点
AnnotationRules	{}	グラフ，辺，頂点の注釈
AspectRatio	Automatic	縦横比
Axes	False	座標軸を描くか描かないか
AxesLabel	None	座標軸のラベル
AxesOrigin	Automatic	座標軸の交点
AxesStyle	{}	座標軸のスタイル指定
Background	None	プロットの背景色
BaselinePosition	Automatic	周囲のテキストのベースラインとの揃え方
BaseStyle	{}	グラフィックスのベーススタイル指定
ContentSelectable	Automatic	コンテンツの選択を許容するかどうか
CoordinatesToolOptions	Automatic	座標ツールの細かな動作
DirectedEdges	Automatic	RuleをDirectedEdgeとして解釈するかどうか
EdgeLabels	None	辺のラベルとその置き方
EdgeLabelStyle	Automatic	辺のラベルのスタイル
EdgeShapeFunction	Automatic	辺のグラフィックス形状を生成する
EdgeStyle	Automatic	辺のスタイル
EdgeWeight	Automatic	辺の重み
Epilog	{}	主となるプロットの後に描くプリミティブ
FormatType	TraditionalForm	テキストのデフォルトの書式
Frame	False	プロットの周囲に枠を描くか描かないか
FrameLabel	None	枠のラベル
FrameStyle	{}	枠線のスタイル指定
FrameTicks	Automatic	枠の目盛
FrameTicksStyle	{}	枠目盛のスタイル指定
GraphHighlight	{}	ハイライトするグラフ要素
GraphHighlightStyle	Automatic	ハイライトするスタイル
GraphLayout	Automatic	辺と頂点をどのように配置するか
GridLines	None	描画する格子線
GridLinesStyle	{}	格子線のスタイル指定
ImageMargins	0.	グラフィックスの周囲に残す余白
ImagePadding	All	ラベル等に余分な充填をどの程度許すか
ImageSize	Automatic	描画するグラフィックスの絶対的サイズ
LabelStyle	{}	ラベルのスタイル指定
Method	Automatic	使用するグラフィックスメソッドの詳細
PerformanceGoal	Automatic	パフォーマンスのどの面について最適化するか
PlotLabel	None	全体的なプロットのラベル
PlotRange	All	含める値の範囲
PlotRangeClipping	False	プロット範囲で切り取るかどうか
PlotRangePadding	Automatic	値の範囲をどの程度充填するか
PlotRegion	Automatic	塗り潰す最終的な表示領域
PlotTheme	$PlotTheme	グラフの全体的なテーマ
PreserveImageOptions	Automatic	同じ画像を新たに描画する際に画像のもとのオプションを保存するかどうか
Prolog	{}	主となるプロットに先駆けて描かれるプリミティブ
RotateLabel	True	枠の y 軸に与えられているラベルを回転させるかどうか
Ticks	Automatic	座標軸の目盛
TicksStyle	{}	座標軸の目盛のスタイル指定
VertexCoordinates	Automatic	頂点座標
VertexLabels	None	頂点のラベルとその置き方
VertexLabelStyle	Automatic	頂点ラベルのスタイル
VertexShape	Automatic	頂点のグラフィックスの形状
VertexShapeFunction	Automatic	頂点のグラフィックス形状を生成する
VertexSize	Medium	頂点の大きさ
VertexStyle	Automatic	頂点のスタイル
VertexWeight	Automatic	頂点の重み

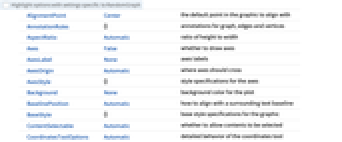
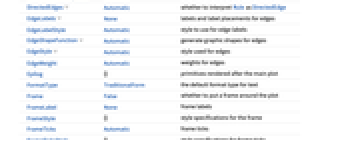
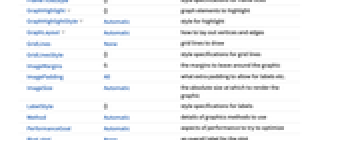
例題

すべて開くすべて閉じる

例 (2)

5個の頂点と6本の辺のランダムグラフを生成する：

グラフ特性の分布のシミュレーションを行う：

スコープ (12)

指定された頂点と辺の数で擬似乱数グラフを生成する：

有向擬似ランダムグラフ：

さまざまなサイズと次数の配列を生成する：

グラフの配列：

Barabasi–Albertモデルに基づいた分布に従うランダムグラフを生成する：

ベルヌーイ(Bernoulli)分布に従うランダムグラフを生成する：

一様分布に従うランダムグラフを生成する：

指定された次数列でランダムグラフを生成する：

ランダム空間グラフを生成する：

Priceモデルによる分布に従うランダムグラフを生成する：

Watts–Strogatzモデルによる分布に従うランダムグラフを生成する：

大きいサイズのランダムグラフを生成する：

オプション (70)

DirectedEdges (1)

デフォルトで，無向グラフが生成される：

DirectedEdges->Trueを使って有向グラフを生成する：

EdgeLabels (6)

辺12にラベルを付ける：

すべての辺にラベルを付ける：

Placedを記号位置と一緒に使って辺に沿ったラベルの置き方を制御する：

明示的な座標を使ってラベルを置く：

ラベル内で位置を変えてみる：

複数のラベルを置く：

TooltipとStatusAreaからの値を使って自動的にラベルを付ける：

EdgeShapeFunction (6)

EdgeShapeFunctionの組込み設定のリストを得る）：

基線を含む無向辺：

辺に異なるグリフがある線グラフ：

実線の矢印を含む有向辺：

線分の矢印：

塗り潰されていない矢印：

個々の辺に辺関数を指定する：

別のデフォルトの辺関数と組み合せる：

プログラムを実行して辺を描画する：

EdgeShapeFunctionはEdgeStyleと組み合せることができる：

EdgeShapeFunctionはEdgeStyleより優先順位が高い：

EdgeStyle (2)

すべての辺にスタイルを付ける：

個々の辺にスタイルを付ける：

GraphHighlight (3)

頂点1をハイライトする：

辺23をハイライトする：

頂点と辺をハイライトする：

GraphHighlightStyle (2)

GraphHighlightStyleの組込み設定のリストを得る：

GraphHighlightStyleの組込み設定を使う：

GraphLayout (4)

デフォルトでレイアウトは自動的に選ばれる：

特殊な曲線のレイアウトを指定する：

最適化基準を満足するレイアウトを指定する：

AbsoluteOptionsを使ってレイアウトアルゴリズムを使って計算されたVertexCoordinatesを抽出する：

PlotTheme (4)

基本テーマ (2)

一般的な基本テーマを使う：

白黒のテーマを使う：

特徴テーマ (2)

大きいグラフのテーマを使う：

古典的な図表テーマを使う：

VertexCoordinates (3)

デフォルトで，任意の頂点座標が自動的に計算される：

AbsoluteOptionsを使って結果の頂点座標を抽出する：

楕円に沿ったレイアウト関数を指定する：

これを使ってグラフの頂点座標を生成する：

VertexCoordinatesはGraphLayoutより優先順位が高い：

VertexLabels (13)

頂点名をラベルとして使う：

個々の頂点にラベルを付ける：

すべての頂点にラベルを付ける：

任意の式をラベルとして使う：

Placedを記号位置と一緒に使って外側の位置も含むラベルの置き方を指定する：

記号的外側コーナー位置：

記号的内側位置：

記号的内側コーナー位置：

明示的な座標を使ってラベルの中心を置く：

すべてのラベルを頂点の右上コーナー位置に置き，ラベル内の座標を変化させる：

複数のラベルを置く：

任意の数のラベルが使える：

Placedの引数を使ってTooltipを含むフォーマットを制御する：

あるいはStatusAreaを含むフォーマットを制御する：

より高度なフォーマット関数を使う：

VertexShape (5)

Graphics，Image，Graphics3Dの任意のものを頂点の形として使う：

個々の頂点の形を指定する：

VertexShapeはVertexSizeと組み合せることができる：

VertexShapeはVertexStyleの影響を受けない：

VertexShapeFunctionはVertexShapeより優先順位が高い：

VertexShapeFunction (9)

組込みのVertexShapeFunctionコレクションのリストを得る：

"Basic"コレクションのVertexShapeFunctionの組込み設定を使う：

簡単な基本形：

一般的な基本形：

"Rounded"コレクションのVertexShapeFunctionの組込み設定を使う：

"Concave"コレクションのVertexShapeFunctionの組込み設定を使う：

個々の頂点を描画する：

デフォルトの頂点関数と組み合せる：

プログラムを実行して頂点を描画する：

VertexShapeFunctionはVertexStyleと組み合せることができる：

VertexShapeFunctionはVertexStyleよりも優先順位が高い：

VertexShapeFunctionはVertexShapeと組み合せることができる：

VertexShapeFunctionはVertexShapeより優先順位が高い：

VertexSize (8)

デフォルトで，頂点の大きさは自動的に計算される：

記号的な頂点サイズを使ってすべての頂点の大きさを指定する：

頂点座標間の最短距離との割合を使う：

すべての頂点座標に対して全体的な対角の割合を使う：

方向と方向の両方に大きさを指定する：

個々の頂点の大きさを指定する：

VertexSizeはVertexShapeFunctionと組み合せることができる：

VertexSizeはVertexShapeと組み合せることができる：

VetexStyle (4)

すべての頂点にスタイルを付ける：

個々の頂点にスタイルを付ける：

VertexShapeFunctionはVertexStyleと組み合せることができる：

VertexShapeFunctionはVertexStyleより優先順位が高い：

VertexStyleはBaseStyleと組み合せることができる：

VertexStyleはBaseStyleより優先順位が高い：

アプリケーション (3)

グラフ分布特性のランダムなでデータを生成し，そのヒストグラムと確率密度関数を比較する：

ベルヌーイ(Bernoulli)グラフの頂点次数が二項分布に従うことを証明する：

各ノードのグループ内のインタラクション数が既知であるとして，インタラクションネットワークのシミュレーションを行う：

特性と関係 (10)

RandomGraphは整数の頂点を使う：

VertexReplaceを使ってグラフの頂点を置換する：

SeedRandomを使って反復可能なランダムグラフを得る：

BlockRandomを使ってRandomGraphの使用が他に影響することを防ぐ：

RandomVariateは確率分布から変量を生成する：

RandomIntegerは離散一様分布に従う確率変量を生成する：

RandomRealは連続一様分布に従う変量を生成する：

RandomChoiceはリストから置き換えるものを選ぶ無作為選択を生成する：

RandomSampleはリストからの置き換えのない無作為選択を生成する：

RandomPrimeはランダムな素数を生成する：

RandomImageはランダムな画像を生成する：

考えられる問題 (1)

n 個の頂点の単純グラフの辺の数は以下である：

RandomGraph[{n,Binomial[n,2]}]は常に n 個の頂点の完全グラフを返す：

おもしろい例題 (1)

ランダムな星座を生成する：

トップへ