TruncatedDistribution

TruncatedDistribution[{xmin,xmax},dist]

表示通过截断 dist 中的值，使之位于 xmin 和 xmax 之间所获得的分布.

TruncatedDistribution[{{xmin,xmax},{ymin,ymax},…},dist]

表示通过截断多变量分布 dist 中的值，使之位于 xmin 和 xmax、ymin 和 ymax、……之间所获得的分布.

更多信息

  • 当 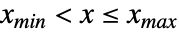时，TruncatedDistribution[{xmin,xmax},dist] 的概率密度为 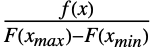，其中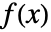 为 概率密度函数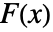， 为 dist 的累积分布函数，其它时候概率密度为零.
  • {xmin,xmax} 的常见情形包括：
  • {-∞,xmax}从上端截断
    {xmin,∞}从下端截断
    {xmin,xmax}双边截断
    {-∞,∞},None不截断
  • TruncatedDistribution 可与 Mean、CDF 和 RandomVariate 等函数联合使用.

背景

  • TruncatedDistribution[{xmin,xmax},dist] 表示一种对数据建模的统计分布，该数据是区间 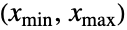中所有 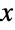的单变量分布 dist 的常数倍数，并且对于 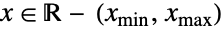恒定为 0. 术语非截断、下截断、上截断和双截断分别用于描述 {xmin,xmax} 具有 {-∞,∞}、{xmin,∞}、{-∞,xmax} 和 {xmin,xmax} 形式的单变量截断，而单变量 dist 可以是连续的（例如 NormalDistribution、GammaDistribution 或 BetaDistribution）或离散的（例如 PoissonDistribution、BinomialDistribution 或 BernoulliDistribution），并且可以根据已知分布的变换、删失或截断（分别通过 TransformedDistribution、CensoredDistribution 和 TruncatedDistribution）来定义.
  • 多变量 TruncatedDistribution[{{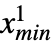,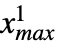},… ,{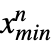,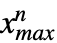}},dist] 的定义与此类似，因此表示从多变量分布 dist 中获取的向量 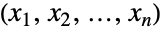的分布，其第 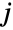个分量 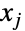被截断为位于区间 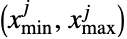内. 与单变量情况一样，多变量 dist 也可以是连续的（例如 MultinormalDistribution）或离散的（例如 MultivariateHypergeometricDistribution），也可以定义为已知分布的 copula 或乘积（分别使用 CopulaDistribution 和ProductDistribution）.
  • 截断分布在数据集包含的值超出“可接受”区间时出现. 例如，如果从 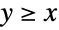名纳税人中选取前 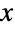名申报所得税的人进行审计，那么对审计后的申报表进行的任何统计分析都将以截断数据的形式出现，前提是没有存储关于避免审计的 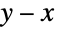名纳税人的信息. 这种数据在生存分析、金融、精算科学和经济学等领域很常见，并且存在各种专门的统计工具（如截断回归）来分析此类数据集.
  • TruncatedDistribution（截断分布）经常与 CensoredDistribution（删失分布）混淆，尽管这两者本质上是不同的，因为截断将概率分布在截断区间内，而删失将全部概率置于删失区间的端点. 根据定义，CensoredDistribution[{xmin,xmax},dist] 等价于 TransformedDistribution[g,xdist]，其中 g 由 Piecewise[{{0,x<=xmin},{h,xmin<x<xmax},{0,x>=xmax}}] 给出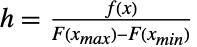，，其中 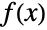是概率密度函数，而 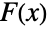是 dist 的累积分布函数.

范例

打开所有单元关闭所有单元

基本范例  (3)

简单的截断分布：

定义一个单变量截断分布：

定义一个多变量截断分布：

范围  (35)

基本用途  (9)

定义单变量连续分布的各种截断：

所得到的概率密度函数在截断区域以外为0：

定义单变量离散分布的各种截断：

不包括左端点，但包括右端点：

定义一个右截断分布：

比较 PDF：

定义一个左截断分布：

比较概率密度函数：

比较均值：

比较标准差：

定义一个双截断分布：

比较均值：

比较方差：

定义一个截断的多变量连续分布：

计算该分布下一个表达式的期望：

求矩量：

定义一个截断的多变量离散分布：

比较截断区域外的点的概率：

生成随机样本：

比较均值：

定义一个截断的多变量离散分布：

比较偏度：

比较峰度：

利用 EstimatedDistribution 估计截断区间：

拟合截断正态分布：

参数分布  (7)

定义一个左截断连续分布：

比较概率密度函数：

截断指数分布的累积分布函数：

统计度量：

与原始分布比较：

定义一个右截断离散分布：

比较概率密度函数：

截断分布与下面相同：

定义 UniformDistribution 的截断：

概率密度函数：

与定义在截断区间上的均匀分布比较：

定义 DiscreteUniformDistribution 的截断：

概率密度函数：

与定义在截断区间上的均匀分布比较：

截断不包括左端点，因此得到的离散分布如下：

定义一个截断的双正态分布：

比较双正态分布与截断分布的概率密度函数：

截断的双正态分布的概率密度函数：

特征函数：

定义一个离散多变量截断分布：

对该分布进行统计运算：

由截断分布生成一组伪随机数：

比较直方图与概率密度函数：

非参数分布  (3)

截断一个 SmoothKernelDistribution：

比较概率密度函数：

定义一个截断的 EmpiricalDistribution：

比较累积分布函数：

定义一个截断的 HistogramDistribution：

概率密度函数：

导出分布  (10)

定义一个截断的 TruncatedDistribution：

求概率密度函数：

识别截断分布：

定义一个截断的 CopulaDistribution：

定义一个截断的 MixtureDistribution：

比较概率密度函数：

定义一个截断的 OrderDistribution：

已知一个泊松样本大于5，求该样本的最大值大于6的概率：

如果没有大于5的假定条件，求该样本的最大值大于6的概率：

定义一个截断的 TransformedDistribution：

比较 与截断正态分布的变换：

定义一个截断的 ParameterMixtureDistribution：

比较概率密度函数：

求两种分布的最大可能值的概率：

定义一个截断的 ProductDistribution：

比较概率密度函数：

比较截断分布乘积的概率密度函数：

定义一个截断的 MarginalDistribution：

比较概率密度函数：

定义一个截断的 CensoredDistribution：

比较概率密度函数：

QuantityDistribution 的截断会计算为 QuantityDistribution：

求平均温度：

自动简化  (6)

连续分布  (4)

GumbelDistribution 在正轴上的截断服从 GompertzMakehamDistribution：

NormalDistribution 在正轴上的截断服从 HalfNormalDistribution：

ParetoDistribution 的截断是封闭的：

UniformDistribution 的截断是封闭的：

离散分布  (2)

DiscreteUniformDistribution 的截断是封闭的：

ZipfDistribution 的截断是封闭的：

应用  (5)

一家杂货店以 每磅的价格订购 磅农产品以在一天中出售，该农产品的销售利润为 每磅. 一天中的销售量服从某一分布 . 未售出的产品在一天结束时将被丢弃. 求使得每日利润最大化的值 ：

假定利润率为30%，并用 LogNormalDistribution 作为销售量的分布：

美国越橘的直径遵循正态分布，直径为16mm，标准偏差为1.6mm. 水果必须至少15mm才可以作为一个整体销售；否则将用于生产越橘酱. 求水果将被作为整体销售的大小分布：

比较概率密度函数：

求销售水果的平均直径：

销售水果直径至少18mm的概率：

可用于控制长尾分布显示的截断分布的一个例子：

拟合数据为帕累托 (Pareto) 分布：

比较样本的直方图和估计分布的概率密度函数：

由于长尾，直方图的范围被调整了，分布被截断：

考虑某种螃蟹的宽度：

拟合数据为 DagumDistribution：

比较直方图和估计分布的概率密度函数：

通常逮到的蟹类大小是在某种范围之内：

拟合数据为左截断的 Dagum 分布：

比较对数似然值，看看与截断分布的拟合结果是否更佳：

一家公司生产指甲长度具有正态分布，其均值为0.5英寸. 假设所生产的指甲50%的长度比均值小0.5英寸，求标准偏差：

标准差就是就是在规范内概率等于50%：

绘制找到的近似值：

标准偏差：

属性和关系  (7)

截断分布等价于在一个区间上的条件分布：

截断分布的概率密度函数仅在截断区间内具有非零值：

比较密度函数：

利用底层分布的性质构建一个截断分布的概率密度函数：

比较一个离散分布的删截与截断：

在截断情况下，截断外部权重在截断区间上均匀分布：

在删截情况下，外部权重位于删截区间的端点：

比较一个连续分布的删截与截断：

在截断情况下，概率在截断区间上均匀分布：

在删截情况下，概率位于删截区间的端点：

GompertzMakehamDistribution 与截断的 WeibullDistribution 相关：

截断的 GumbelDistribution 即 GompertzMakehamDistribution：

巧妙范例  (1)

双变量分布的双重截断：

Wolfram Research (2010)，TruncatedDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TruncatedDistribution.html （更新于 2016 年）.

文本

Wolfram Research (2010)，TruncatedDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TruncatedDistribution.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "TruncatedDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/TruncatedDistribution.html.

APA

Wolfram 语言. (2010). TruncatedDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TruncatedDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_truncateddistribution, author="Wolfram Research", title="{TruncatedDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/TruncatedDistribution.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_truncateddistribution, organization={Wolfram Research}, title={TruncatedDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/TruncatedDistribution.html}, note=[Accessed: 14-November-2024 ]}