NMinValue[f,x]
gives the global minimum value of f with respect to x.
NMinValue[f,{x,y,…}]
gives the global minimum value of f with respect to x, y, ….
NMinValue[{f,cons},{x,y,…}]
gives the global minimum value of f subject to the constraints cons.
NMinValue[…,x∈reg]
constrains x to be in the region reg.




NMinValue
NMinValue[f,x]
gives the global minimum value of f with respect to x.
NMinValue[f,{x,y,…}]
gives the global minimum value of f with respect to x, y, ….
NMinValue[{f,cons},{x,y,…}]
gives the global minimum value of f subject to the constraints cons.
NMinValue[…,x∈reg]
constrains x to be in the region reg.
Details and Options





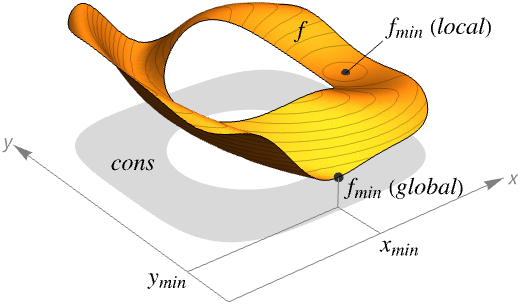
- NMinValue is also known as global optimization (GO).
- NMinValue always attempts to find a global minimum of f subject to the constraints given.
- NMinValue is typically used to find the smallest possible values given constraints. In different areas, this may be called the best strategy, best fit, best configuration and so on.
- If f and cons are linear or convex, the result given by NMinValue will be the global minimum, over both real and integer values; otherwise, the result may sometimes only be a local minimum.
- If NMinValue determines that the constraints cannot be satisfied, it returns Infinity.
- NMinValue supports a modeling language where the objective function f and constraints cons are given in terms of expressions depending on scalar or vector variables. f and cons are typically parsed into very efficient forms, but as long as f and the terms in cons give numerical values for numerical values of the variables, NMinValue can often find a solution.
- The constraints cons can be any logical combination of:
-
lhs==rhs equations lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs inequalities (LessEqual, …) lhsrhs, lhsrhs, lhsrhs, lhsrhs vector inequalities (VectorLessEqual, …) {x,y,…}∈rdom region or domain specification - NMinValue[{f,cons},x∈rdom] is effectively equivalent to NMinValue[{f,cons&&x∈rdom},x].
- For x∈rdom, the different coordinates can be referred to using Indexed[x,i].
- Possible domains rdom include:
-
Reals real scalar variable Integers integer scalar variable Vectors[n,dom] vector variable in 
Matrices[{m,n},dom] matrix variable in 
ℛ vector variable restricted to the geometric region 
- By default, all variables are assumed to be real.
- The following options can be given:
-
AccuracyGoal Automatic number of digits of final accuracy sought EvaluationMonitor None expression to evaluate whenever f is evaluated MaxIterations Automatic maximum number of iterations to use Method Automatic method to use PrecisionGoal Automatic number of digits of final precision sought StepMonitor None expression to evaluate whenever a step is taken WorkingPrecision MachinePrecision the precision used in internal computations - The settings for AccuracyGoal and PrecisionGoal specify the number of digits to seek in both the value of the position of the minimum, and the value of the function at the minimum.
- NMinValue continues until either of the goals specified by AccuracyGoal or PrecisionGoal is achieved.
- The methods for NMinValue fall into two classes. The first class of guaranteed methods uses properties of the problem so that, when the method converges, the minimum found is guaranteed to be global. The second class of heuristic methods uses methods that may include multiple local searches, commonly adjusted by some stochasticity, to home in on a global minimum. These methods often do find the global minimum, but are not guaranteed to do so.
- Methods that are guaranteed to give a global minimum when they converge to a solution include:
-
"Convex" use only convex methods "MOSEK" use the commercial MOSEK library for convex problems "Gurobi" use the commercial Gurobi library for convex problems "Xpress" use the commercial Xpress library for convex problems - Heuristic methods include:
-
"NelderMead" simplex method of Nelder and Mead "DifferentialEvolution" use differential evolution "SimulatedAnnealing" use simulated annealing "RandomSearch" use the best local minimum found from multiple random starting points "Couenne" use the Couenne library for non-convex mixed-integer nonlinear problems
Examples
open all close allBasic Examples (4)
Scope (40)
Basic Uses (12)
Find the minimum value of ![]() subject to constraints
subject to constraints ![]() :
:
Several linear inequality constraints can be expressed with VectorGreaterEqual:
Use ![]() v>=
v>=![]() or \[VectorGreaterEqual] to enter the vector inequality sign :
or \[VectorGreaterEqual] to enter the vector inequality sign :
An equivalent form using scalar inequalities:
The inequality ![]() may not be the same as
may not be the same as ![]() due to possible threading in
due to possible threading in ![]() :
:
To avoid unintended threading in ![]() , use Inactive[Plus]:
, use Inactive[Plus]:
Use constant parameter equations to avoid unintended threading in ![]() :
:
VectorGreaterEqual represents a conic inequality with respect to the "NonNegativeCone":
To explicitly specify the dimension of the cone, use {"NonNegativeCone",n}:
Find the minimum value of ![]() subject to the constraint
subject to the constraint ![]() :
:
Specify the constraint ![]() using a conic inequality with "NormCone":
using a conic inequality with "NormCone":
Find the minimum value of the function ![]() subject to the constraint
subject to the constraint ![]() :
:
Use Indexed to access components of a vector variable, e.g. ![]() :
:
Use Vectors[n,dom] to specify the dimension and domain of a vector variable when it is ambiguous:
Specify non-negative constraints using NonNegativeReals (![]() ):
):
An equivalent form using vector inequality ![]() :
:
Specify non-positive constraints using NonPositiveReals (![]() ):
):
An equivalent form using vector inequalities:
Or constraints can be specified:
Domain Constraints (4)
Specify integer domain constraints using Integers:
Specify integer domain constraints on vector variables using Vectors[n,Integers]:
Specify non-negative integer domain constraints using NonNegativeIntegers (![]() ):
):
Specify non-positive integer domain constraints using NonPositiveIntegers (![]() ):
):
Region Constraints (5)
Find the minimum value of ![]() over a region:
over a region:
Find the minimum distance between two regions:
Find the minimum of ![]() such that the triangle and ellipse still intersect:
such that the triangle and ellipse still intersect:
Find the minimum radius of a disk that contains the given three points:
Using Circumsphere gives the same result directly:
Linear Problems (5)
With linear objectives and constraints, when a minimum is found it is global:
The constraints can be equality and inequality constraints:
Use Equal to express several equality constraints at once:
An equivalent form using several scalar equalities:
Use VectorLessEqual to express several LessEqual inequality constraints at once:
Use ![]() v<=
v<=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
An equivalent form using scalar inequalities:
Use Interval to specify bounds on variable:
Convex Problems (7)
Use "NonNegativeCone" to specify linear functions of the form ![]() :
:
Use ![]() v>=
v>=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
Find the minimum value of a convex quadratic function subject to linear constraints:
Find the minimum value of a convex quadratic function subject to a set of convex quadratic constraints:
Find the minimum distance between two convex regions:
Find the minimum value of ![]() such that
such that ![]() is positive semidefinite:
is positive semidefinite:
Minimize convex objective function ![]() such that
such that ![]() is positive semidefinite and
is positive semidefinite and ![]() :
:
Find the minimum value of a convex objective function over a 4-norm unit disk:
Transformable to Convex (4)
Find the minimum perimeter of a rectangle with area 1 such that the height is at most half the width:
This problem is log-convex and is solved by making a transformation {hExp[],wExp[ ]} and taking logarithms to get the convex problem:
Find the minimum value of the quasi-convex function ![]() subject to inequality and norm constraints. The objective is quasi-convex because it is a product of a non-negative function and a non-positive function over the domain:
subject to inequality and norm constraints. The objective is quasi-convex because it is a product of a non-negative function and a non-positive function over the domain:
Quasi-convex problems can be solved as parametric convex optimization problems for the parameter ![]() :
:
Plot the objective as a function of the level-set ![]() :
:
For a level-set value between the interval ![]() , the smallest objective is found:
, the smallest objective is found:
The problem becomes infeasible when the level-set value is increased:
Minimize ![]() subject to the constraint
subject to the constraint ![]() . The objective is not convex but can be represented by a difference of convex function
. The objective is not convex but can be represented by a difference of convex function ![]() where
where ![]() and
and ![]() are convex functions:
are convex functions:
Plot the region and the minimizing point:
Minimize ![]() subject to the constraints
subject to the constraints ![]() . The constraint
. The constraint ![]() is not convex but can be represented by a difference of convex constraint
is not convex but can be represented by a difference of convex constraint ![]() where
where ![]() are convex functions:
are convex functions:
Options (7)
AccuracyGoal & PrecisionGoal (2)
This enforces convergence criteria ![]() and
and ![]() :
:
This enforces convergence criteria ![]() and
and ![]() , which is not achievable with the default machine-precision computation:
, which is not achievable with the default machine-precision computation:
Setting a high WorkingPrecision makes the process convergent:
EvaluationMonitor (1)
Method (2)
StepMonitor (1)
Steps taken by NMinValue in finding the minimum of the classic Rosenbrock function:
WorkingPrecision (1)
With the working precision set to ![]() , by default AccuracyGoal and PrecisionGoal are set to
, by default AccuracyGoal and PrecisionGoal are set to ![]() :
:
Applications (6)
Geometry Problems (3)
Find the minimum distance between two disks of radius 1 centered at ![]() and
and ![]() . Let
. Let ![]() be a point on disk 1. Let
be a point on disk 1. Let ![]() be a point on disk 2. The objective is to minimize
be a point on disk 2. The objective is to minimize ![]() subject to constraints
subject to constraints ![]() :
:
Find the radius ![]() of a minimal enclosing ball that encompasses a given region:
of a minimal enclosing ball that encompasses a given region:
Find the minimum value of the radius ![]() subject to the constraints
subject to the constraints ![]() :
:
The minimal enclosing ball can be found efficiently using BoundingRegion:
Find the smallest square that can contain ![]() circles of given radius
circles of given radius ![]() for
for ![]() that do not overlap. Specify the number of circles and the radius of each circle:
that do not overlap. Specify the number of circles and the radius of each circle:
If ![]() is the center of circle
is the center of circle ![]() , then the objective is to minimize
, then the objective is to minimize ![]() . The objective can be transformed so as to minimize
. The objective can be transformed so as to minimize ![]() and
and ![]() :
:
Data-Fitting Problems (1)
Find the Gaussian width parameter ![]() that minimizes the residual for an
that minimizes the residual for an ![]() fit to nonlinear discrete data:
fit to nonlinear discrete data:
Fit the data using the basis ![]() :
:
The function will be approximated by ![]() :
:
Construct a parametric function that gives the residual:
Show the residual as a function of ![]() :
:
Find the scaling parameter that produces the minimum residual:
Iterated Optimization (1)
Trajectory Optimization (1)
Find the minimum length of a path between the start and end points while avoiding circular obstacles:
The path is discretized into ![]() different points. The distance between these points must be less than
different points. The distance between these points must be less than ![]() where
where ![]() is the length to be minimized:
is the length to be minimized:
The points cannot be inside the circular objects:
Properties & Relations (8)
NMinimize gives the minimum value and rules for the minimizing values of the variables:
NArgMin gives a list of the minimizing values:
NMinValue gives only the minimum value:
Maximizing a function f is equivalent to minimizing -f:
For convex problems, ConvexOptimization may be used to obtain additional solution properties:
For convex problems with parameters, using ParametricConvexOptimization gives a ParametricFunction:
The ParametricFunction may be evaluated for values of the parameter:
Define a function for the parametric problem using NMinValue:
Compare the speeds of the two approaches:
Derivatives of the ParametricFunction can also be computed:
For convex problems with parametric constraints, RobustConvexOptimization finds an optimum that works for all possible values of the parameters:
NMinValue may find a smaller minimum value for particular values of the parameters:
The minimizer that gives this value does not satisfy the constraints for all allowed values of ![]() and
and ![]() :
:
The minimum value found for particular values of the parameters is less than or equal to the robust minimum:
NMinValue can solve linear programming problems:
LinearProgramming can be used to solve the same problem given in matrix notation:
Use RegionDistance to compute the minimum distance from a point to a region:
Compute the distance using NMinValue:
Use RegionBounds to compute the bounding box:
Related Guides
History
Introduced in 2008 (7.0) | Updated in 2014 (10.0) ▪ 2021 (12.3) ▪ 2021 (13.0) ▪ 2022 (13.2) ▪ 2024 (14.1)
Text
Wolfram Research (2008), NMinValue, Wolfram Language function, https://reference.wolfram.com/language/ref/NMinValue.html (updated 2024).
CMS
Wolfram Language. 2008. "NMinValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/NMinValue.html.
APA
Wolfram Language. (2008). NMinValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NMinValue.html
BibTeX
@misc{reference.wolfram_2025_nminvalue, author="Wolfram Research", title="{NMinValue}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NMinValue.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_nminvalue, organization={Wolfram Research}, title={NMinValue}, year={2024}, url={https://reference.wolfram.com/language/ref/NMinValue.html}, note=[Accessed: 06-March-2026]}