ChiSquareDistribution

ChiSquareDistribution[ν]

自由度 ν のカイ二乗()分布を表す．

詳細

  • カイ二乗分布における値 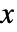の確率密度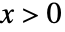は，のときは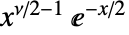に比例し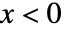，のときは0である． »
  • 整数 ν ついては，自由度が ν のカイ二乗分布は正規分布から独立にサンプルした ν の値の平方和の分布を与える．
  • ChiSquareDistributionでは，ν は任意の正の実数でよい．
  • ChiSquareDistributionでは，ν は無次元量でよい． »
  • ChiSquareDistributionは，Mean，CDF，RandomVariate等の関数で使うことができる． »

予備知識

  • ChiSquareDistribution[ν]は，分布の自由度を表す正の値 ν でパラメータ化された統計分布を表す．ν はカイ二乗分布の確率密度関数(PDF)の一般的な形を決定し，ν の値によって，確率密度関数は，単調減少になるか，潜在的特異値が領域の下方境界に近付く単一の「峰」（大域最大値）を持つようになるかする．
  • ChiSquareDistributionは，カイ分布に従う確率変数の二乗が従う分布である．つまり，もし 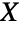が確率変数であり 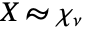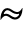（ は「として分布する」の意）であるなら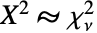，である．同一正規分布に従う独立確率変数の集合 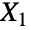, , 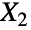…, 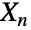の総和 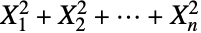もまたカイ二乗分布に従う．カイ二乗分布は，理論的あるいは経験的モデルとサンプル集合との間の自由度の数量化に使うことができる．具体的な適用分野として，磁気共鳴画像法，疾病に触れることと伝染との考えられる関連の分析等がある．
  • RandomVariateを使って，カイ二乗分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,ChiSquareDistribution[ν]]（より簡略すると xChiSquareDistribution[ν]）を使って，確率変数 x がカイ二乗分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • カイ二乗分布の確率密度関数および累積分布関数は，PDF[ChiSquareDistribution[ν],x]およびCDF[ChiSquareDistribution[ν],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がカイ二乗分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックカイ二乗分布を推定することが，FindDistributionParametersを使ってデータをカイ二乗分布にフィットすることができる．ProbabilityPlotを使って記号カイ二乗分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号カイ二乗分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたカイ二乗分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってカイ二乗分布を含む高次元分布を構築することが，ProductDistributionを使ってカイ二乗分布を含む独立成分分布の結合分布を計算することができる．
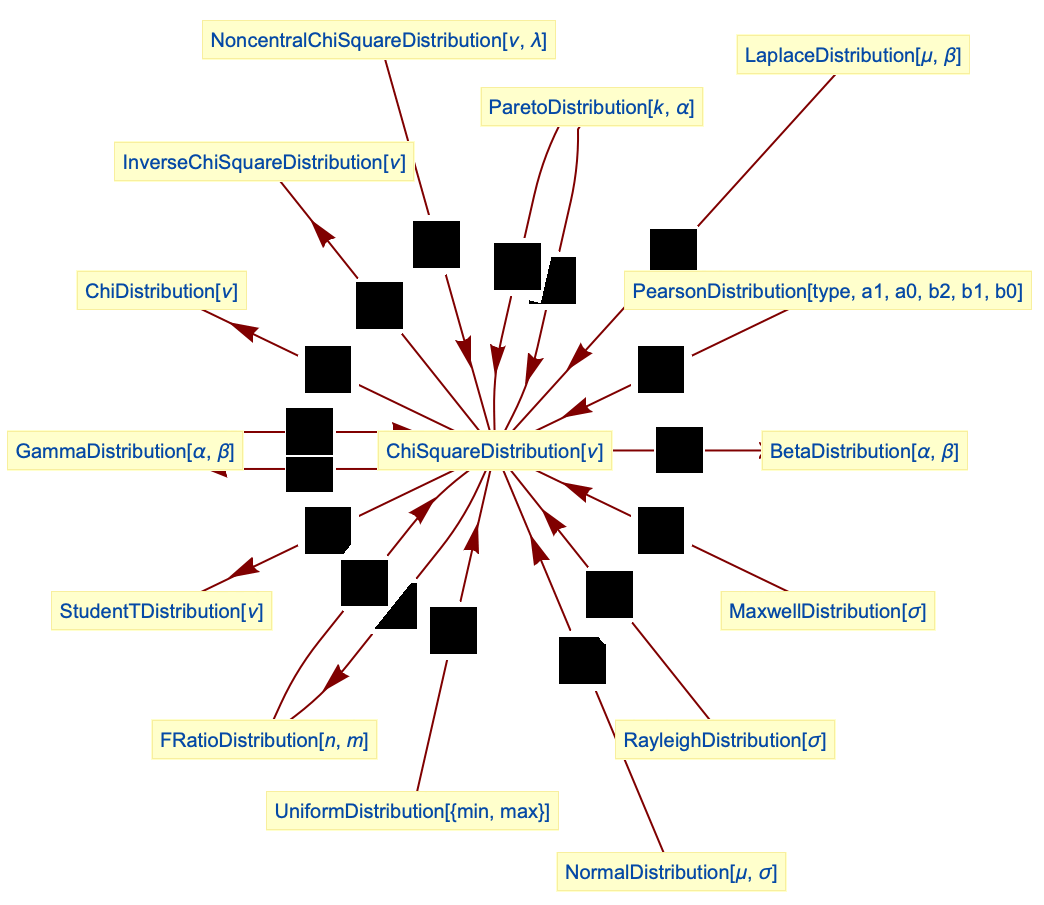
  • ChiSquareDistributionは他の数多くの分布と関連している．例えば，GammaDistribution，ExponentialDistribution，InverseChiSquareDistribution，UniformDistribution，LaplaceDistributionを含むいくつかの分布は，ChiSquareDistributionの変換として得ることができ，NormalDistributionおよびFRatioDistributionはChiSquareDistributionの変換バージョンの極限値である．さらに，ChiSquareDistributionは，RayleighDistribution，MaxwellDistribution，PearsonDistribution，ParetoDistributionを含む数多くの他のより一般的な関数の特殊形であると見ることができる．ChiSquareDistributionは，BetaDistribution，StudentTDistribution，UniformDistribution，NoncentralChiSquareDistributionとも密接な関係がある．

例題

すべて開くすべて閉じる

例  (4)

確率密度関数：

累積分布関数：

平均と分散：

中央値：

スコープ  (8)

カイ二乗分布から擬似乱数のサンプルを生成する：

このヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度：

自由度が大きくなると分布は対称になる：

尖度：

極限値はNormalDistributionの尖度である：

母数の関数としての閉形式の種々のモーメント：

Moment：

記号次数の閉形式：

CentralMoment：

記号次数の閉形式：

FactorialMoment：

Cumulant：

Cumulantには閉形式がある：

ハザード関数：

分位関数：

無次元Quantityを使って自由度母数 ν を指定する：

アプリケーション  (2)

ChiSquareDistributionは厳密な（小さい）サンプリング理論に使われる．統計を定義する：

データがNormalDistributionに従っているのであれば，統計はデータのサンプルサイズが小さいもの（30未満）であってもChiSquareDistributionに従う：

特定の箱入りのシリアルの重み（単位：グラム）は正規分布に従うことが知られている．品質管理部が15箱を無作為に抽出し重みを記録した．製品の重みの標準偏差が36未満であるという仮定を調べる：

という帰無仮説の下では次の統計はChiSquareDistributionに従う：

帰無仮説は5%で棄却されない：

製品の重みの標準偏差が32に等しいと仮定して，検定の検出力としても知られる帰無仮説をサンプルサイズの関数として5%レベルで棄却する確率を計算する：

検定の検出力が少なくても80%であるために必要なサンプルサイズを求める：

特性と関係  (23)

ChiSquareDistribution[ν]は ν->∞で正規分布に収束する：

カイ二乗分布に従う変数の総和はカイ二乗分布に従う：

他の分布との関係：

NoncentralChiSquareDistributionを簡約するとカイ二乗分布になる：

カイ二乗分布はFRatioDistributionの極限の場合である：

カイ二乗分布に従う2つの変数の割合はFRatioDistributionに従う：

個のNormalDistributionに従う変数の平方和はカイ二乗分布に従う：

カイ二乗分布はGammaDistributionの特殊ケースである：

スケールされたカイ二乗分布はGammaDistributionに従う：

カイ二乗変数の二乗根はChiDistributionに従う：

のRayleighDistributionの平方はカイ二乗分布の特殊なケースである：

のMaxwellDistributionの平方はカイ二乗分布の特殊なケースである：

カイ二乗分布とInverseChiSquareDistributionは互いに逆の関係にある：

カイ二乗分布はタイプ3のピアソン分布(PearsonDistribution)の特殊なケースである：

カイ二乗分布を変換するとBetaDistributionになる：

カイ二乗分布はUniformDistributionを変換したものである：

カイ二乗分布はLaplaceDistributionを変換したものである：

個の変数の和について：

カイ二乗分布はParetoDistributionを変換したものである：

カイ二乗分布はParetoDistributionを変換したものである：

StudentTDistributionはカイ二乗分布を変換したものである：

StudentTDistributionはChiSquareDistributionとNormalDistributionから得られる：

NoncentralBetaDistributionはChiSquareDistributionとNoncentralChiSquareDistributionの変換として得られる：

NoncentralStudentTDistributionはNormalDistributionとChiSquareDistributionから得られる：

考えられる問題  (2)

ChiSquareDistributionは，ν が正の実数でないときは定義されない：

記号出力に無効な母数値を代入すると意味のない結果となる：

おもしろい例題  (1)

累積分布関数の等高線を持つ ν のさまざまな値についての確率密度関数：

Wolfram Research (2007), ChiSquareDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ChiSquareDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2007), ChiSquareDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ChiSquareDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2007. "ChiSquareDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ChiSquareDistribution.html.

APA

Wolfram Language. (2007). ChiSquareDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ChiSquareDistribution.html

BibTeX

@misc{reference.wolfram_2024_chisquaredistribution, author="Wolfram Research", title="{ChiSquareDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ChiSquareDistribution.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_chisquaredistribution, organization={Wolfram Research}, title={ChiSquareDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ChiSquareDistribution.html}, note=[Accessed: 14-November-2024 ]}