ClusteringTree
ClusteringTree[{e1,e2,…}]
构建元素 e1、e2、…等的分级聚类的加权树.
ClusteringTree[{e1v1,e2v2,…}]
在构建的图中用 vi 表示 ei.
ClusteringTree[{e1,e2,…}{v1,v2,…}]
在构建的图中用 vi 表示 ei.
ClusteringTree[label1e1,label2e2…]
在构建的图中用标签 labeli 表示 ei.
ClusteringTree[data,h]
通过把距离小于 h 的子聚类连在一起,根据 data 的分级聚类构建加权树.
更多信息和选项


- 数据元素 ei 可以是数字;数值列表、矩阵或张量;布尔元素列表;字符串或图像;地理位置或地理实体;颜色;以及这些数据的组合. 如果 ei 是列表、矩阵或张量,它们的维度必须相同.
- 来自 ClusteringTree 的结果是一个二项加权树,其中每个顶点的权重表示由该顶点作为根的两个子树之间的距离:
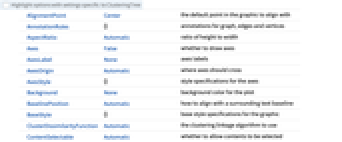
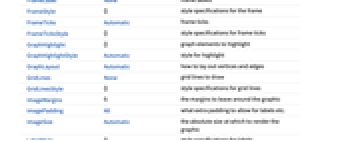
- ClusteringTree 具有与 Graph 相同的选项,并有以下增加和变化: [所有选项的列表]
-
ClusterDissimilarityFunction Automatic 要使用的聚类关联算法 DistanceFunction Automatic 要使用的距离或相异度 EdgeStyle GrayLevel[0.65] 边的样式 FeatureExtractor Automatic 怎样从数据中提取特征 VertexSize 0 顶点的大小 - 缺省情况下,除非指定了 DistanceFunction 或 FeatureExtractor,ClusteringTree 将自动对数据进行预处理.
- ClusterDissimilarityFunction 定义聚类内的相异度,不同成员元素之间的相异度已知.
- ClusterDissimilarityFunction 的可能设置包括:
-
"Average" 平均聚类内相异度 "Centroid" 聚类质心的距离 "Complete" 最大的聚类内相异度 "Median" 到聚类中位数的距离 "Single" 最小的聚类内相异度 "Ward" Ward 最小方差相异度 "WeightedAverage" 加权平均聚类内相异度 纯函数 - 函数 f 定义了任意两个聚类之间的距离.
- 函数 f 必须是 DistanceMatrix 的实值函数.
所有选项的列表


范例
打开所有单元关闭所有单元基本范例 (5)
范围 (8)
通过 VertexWeight 查看子聚类之间的距离:
根据 Association 计算层次聚类:
与 Values 的层次聚类进行比较:
与 Keys 的层次聚类进行比较:
改变 ClusteringTree 的样式和布局:
选项 (3)
ClusterDissimilarityFunction (1)
DistanceFunction (1)
使用一个不同的 DistanceFunction 获取聚类层次结构:
FeatureExtractor (1)
文本
Wolfram Research (2016),ClusteringTree,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ClusteringTree.html (更新于 2017 年).
CMS
Wolfram 语言. 2016. "ClusteringTree." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/ClusteringTree.html.
APA
Wolfram 语言. (2016). ClusteringTree. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ClusteringTree.html 年