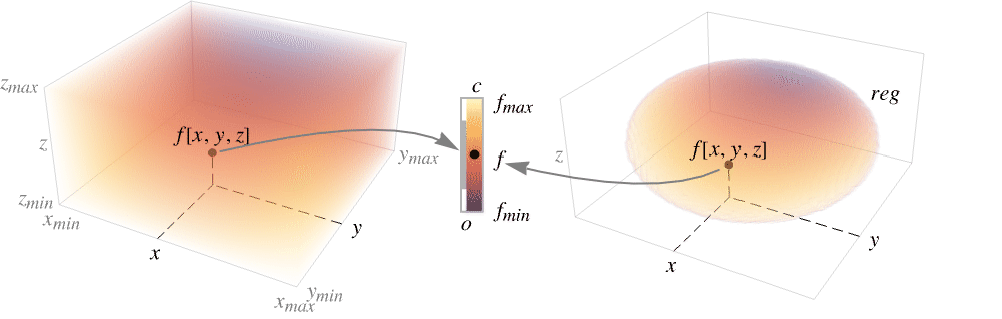
DensityPlot3D[f,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
x,y,z の関数としての f の密度プロットを作成する.
DensityPlot3D[f,{x,y,z}∈reg]
変数が幾何学領域 reg にあるものとする.




DensityPlot3D
DensityPlot3D[f,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
x,y,z の関数としての f の密度プロットを作成する.
DensityPlot3D[f,{x,y,z}∈reg]
変数が幾何学領域 reg にあるものとする.
詳細とオプション


- DensityPlot3Dはボリューム地図としても知られている.
- DensityPlot3Dは関数
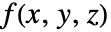 をその領域上で評価し,値を色と不透明度に個別にマップする.
をその領域上で評価し,値を色と不透明度に個別にマップする. - 不透明度関数
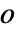 は,通常,ある範囲の値を可視化し他の値を不可視にするために使われる.
は,通常,ある範囲の値を可視化し他の値を不可視にするために使われる. - 以下のプロットは集合
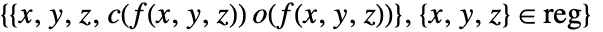 を可視化する.ただし,
を可視化する.ただし,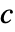 は色関数で
は色関数で 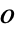 は不透明度の関数である.
は不透明度の関数である. - f を評価しても実数にならない位置は,データが欠けているとみなされ,透過的に描かれる.
- DensityPlot3Dは,事実上Blockを使って変数 x,y,z を局所的なものとして扱う.
- DensityPlot3Dは属性HoldAllを有し,x,y,z に特定の数値を割り当てた後ではじめて f を評価する.
- 場合によってはEvaluateを使って,x,y,z に特定の数値が割り当てられる前に f を記号的に評価した方が効率的なことがある.
- DensityPlot3Dには,Graphics3Dと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
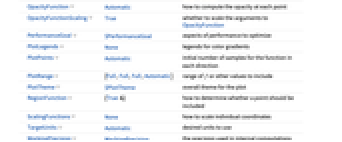
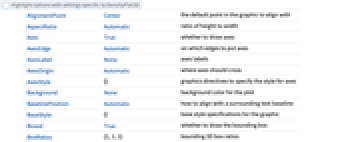
Axes True 軸を描くかどうか BoxRatios {1,1,1} 境界3Dボックスの比 ColorFunction Automatic プロットにどのように彩色するか ColorFunctionScaling True ColorFunctionの引数をスケールするかどうか OpacityFunction Automatic 各点での不透過性をどのように計算するか OpacityFunctionScaling True OpacityFunctionの引数をスケールするかどうか PerformanceGoal $PerformanceGoal パフォーマンスのどの面について最適化するか PlotLegends None 色勾配の凡例 PlotPoints Automatic 各方向の関数のサンプルの初期数 PlotRange {Full,Full,Full,Automatic} 含めるべき f のあるいは他の値の範囲 PlotTheme $PlotTheme プロットの全体的なテーマ RegionFunction (True&) 点を含めるかどうかをどのように決定するか ScalingFunctions None 個々の座標のスケール方法 TargetUnits Automatic 所望の使用単位 WorkingPrecision MachinePrecision 内部計算に使用する精度 - ColorFunctionおよびOpacityFunctionには,デフォルトで,f のスケールされた値で与えられる1引数が与えられる.
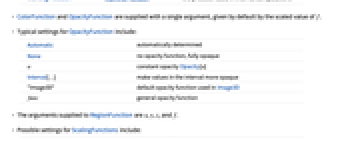
- OpacityFunctionのよく使われる設定
-
Automatic 自動的に決定 None 不透明度関数を使わず,完全に不透明 α 一定の不透明度Opacity[α] Interval[…] 区間の中の値をより不透明にする "Image3D" Image3Dで使われるデフォルトの不透明度関数 func 一般的な不透明度関数 - RegionFunctionに与えられる引数は,x,y,z,f である.
- 次は,ScalingFunctionsの可能な設定である.
-
sf f 等高線の値をスケールする {sx,sy,sz} x,y, z の各軸をスケールする {sx,sy,sz,sf} x,y, z の各軸と f 等高線の値をスケールする - 次は,よく使われる組込みのスケーリング関数 s である.
-
"Log" 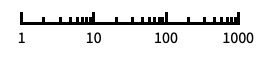
自動的に目盛ラベルを付ける対数スケール "Log10" 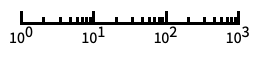
10のベキ乗に目盛を置く,10を底とした対数スケール "SignedLog" 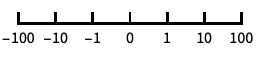
0と負の数を含む対数に似たスケール "Reverse" 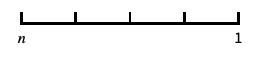
座標の向きを逆にする "Infinite" 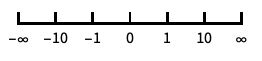
無限スケール
全オプションのリスト



例題
すべて開く すべて閉じるスコープ (13)
サンプリング (6)
PlotPointsを使ってサンプリングを制御する:
領域はConeを含む領域で指定することができる:
ImplicitRegionを含む数式定義領域:
BoundaryMeshRegionを含む,メッシュに基づいた領域:
PlotRangeを使ってより詳細が露出されるように範囲を限定する:
ClipPlanesを使って1つあるいは複数の切り取り平面を指定する.この場合は ![]() を切り取る:
を切り取る:
RegionFunctionを使って点の含み方をより一般的に制約する:
プレゼンテーション (7)
PlotThemeを使って即座に全体的なスタイリングを得る:
PlotLegendsを使って異なる値のための色の棒を得る:
Axesで軸の表示を制御する:
AxesLabelを使って軸に,PlotLabelを使ってプロット全体にラベルを付ける:
ColorFunctionを使い,関数の値でプロットに彩色する:
TargetUnitsは可視化に使う単位を指定する:
オプション (69)
Axes (4)
AxesLabel (4)
ClipPlanes (3)
ColorFunctionScaling (2)
ImageSize (7)
OpacityFunction (6)
OpacityFunctionは,デフォルトでAutomaticである:
OpacityFunctionNoneで透過性をオフにする:
一定の不透明度Opacity[0.05]を使う:
Image3Dで使われているものと同じ不透明度関数を使う:
OpacityFunctionScaling (3)
PlotLegends (2)
ScalingFunctions (4)
デフォルトで,DensityPlot3Dはすべての方向に線形スケールを使う:
ScalingFunctionsを使って ![]() 方向の座標の向きを逆にする:
方向の座標の向きを逆にする:
TargetUnits (2)
Ticks (6)
アプリケーション (17)
初等関数 (4)
分布関数 (6)
分布のPDFをプロットする:
分布のCDFをプロットする:
MultinormalDistributionについてのCorrelationパラメータを調べる.ただし,ρabはa と b との相関である:
y と z の間のみの,z 成分中のより大きい分散 ![]() のある相関:
のある相関:
ProductDistributionのPDFを可視化する:
CopulaDistributionのPDFをプロットする:
ある三変量データのカーネル密度推定のPDFを可視化する:
ClipPlanesを使って中心を通してみる:
偏微分方程式 (3)
非線形sine-Gordon方程式を周期的境界条件を持ち ![]() 軸に沿って時間を表現された2つの空間次元で可視化する:
軸に沿って時間を表現された2つの空間次元で可視化する:
Wolframの非線形波動方程式を,時間が ![]() 軸に沿って表された2つの空間次元で可視化する:
軸に沿って表された2つの空間次元で可視化する:
3D偏微分方程式の解を可視化する.この場合は,Ballとディリクレ(Dirichlet)境界条件上でのポアソン(Poisson)方程式:
特性と関係 (5)
データにListDensityPlot3Dを使う:
2D密度プロットにDensityPlotを使う:
SliceDensityPlot3Dをスライス面上の密度プロットに使う:
SliceContourPlot3Dをスライス面上の等高線プロットに使う:
ContourPlot3Dを値が一定の面について使う:
テキスト
Wolfram Research (2015), DensityPlot3D, Wolfram言語関数, https://reference.wolfram.com/language/ref/DensityPlot3D.html (2022年に更新).
CMS
Wolfram Language. 2015. "DensityPlot3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/DensityPlot3D.html.
APA
Wolfram Language. (2015). DensityPlot3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DensityPlot3D.html
BibTeX
@misc{reference.wolfram_2025_densityplot3d, author="Wolfram Research", title="{DensityPlot3D}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/DensityPlot3D.html}", note=[Accessed: 19-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_densityplot3d, organization={Wolfram Research}, title={DensityPlot3D}, year={2022}, url={https://reference.wolfram.com/language/ref/DensityPlot3D.html}, note=[Accessed: 19-January-2026]}