a.b.c またはDot[a,b,c]
ベクトルや行列,テンソルの積を与える.


Dot 
a.b.c またはDot[a,b,c]
ベクトルや行列,テンソルの積を与える.
詳細

- a.b は,a と b が適切な次元を持ったリストであるときに,具体的な結果を与える.a の最後の指数を b の最初の指数で縮約する.
- Dotの応用例
-
{a1,a2}.{b1,b2} ベクトルのスカラー積 {a1,a2}.{{m11,m12},{m21,m22}}ベクトルと行列の積 {{m11,m12},{m21,m22}}.{a1,a2}行列とベクトルの積 {{m11,m12},{m21,m22}}.{{n11,n12},{n21,n22}}2個の行列の積 - Dotを2個のテンソル
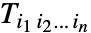 および
および 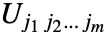 に適用した結果は,やはりテンソルで
に適用した結果は,やはりテンソルで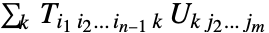 となる.Dotを
となる.Dotを 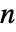 階のテンソルと
階のテンソルと 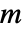 階のテンソルに適用すると,
階のテンソルに適用すると,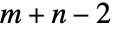 階のテンソルが与えられる. »
階のテンソルが与えられる. » - Dotは,SparseArrayオブジェクトおよび構造化配列オブジェクトに使うことができる.可能な場合は入力と同じタイプのオブジェクトが返される. »
- Dotはすべての引数において線形である. » ベクトルに対して複素(ハミルトン)内積を定義はしない. »
- 引数がリストや疎な配列ではない場合,Dotは未評価でおかれる.DotはFlat属性を持つ.
例題
すべて開く すべて閉じる例 (4)
スコープ (28)
ベクトルのドット積 (7)
Dotには複素入力も使えるが,それらのいずれも共役しない:
複素(エルミート)内積の計算をする場合は,Conjugateを入力の一つに適用するとよい:
参考文献,特に数学文献の中には,第2引数を共役させるものもある:
Normを使って結果を確かめる:
2つのQuantityArrayベクトルのスカラー積を計算する:
行列とベクトルの乗算 (5)
行列と行列の乗算 (11)

CenteredInterval行列の積:
m と n のランダムな代表である mrep と nrep を求める:
mn に mrep と nrep の積が含まれることを確認する:
MatrixPowerと比較する:
DotをApply (@@)およびConstantArrayと組み合せて行列を10乗する:
高階配列 (5)
Dotは任意の階数の配列に使うことができる:
積が共通の次元で行われている限り,任意の組合せを使うことができる:
![]() は,
は,![]() を
を ![]() の最後のレベルと,
の最後のレベルと,![]() を最初のレベルとペアにする完全な縮約
を最初のレベルとペアにする完全な縮約 ![]() である:
である:
![]() は,
は,![]() を
を ![]() の最初のレベルと,
の最初のレベルと,![]() を最後のレベルとペアにする別の縮約
を最後のレベルとペアにする別の縮約 ![]() である:
である:
mの両方のレベルをaの2番目と3番目のレベルでそれぞれ縮約する:
2つの疎な配列のDotは,一般に,別の疎な配列である:
疎な配列と通常のリストのDotは,別の疎な配列または通常のリストかもしれない:
2つのSymmetrizedArrayオブジェクトの積は,一般に,別の対称化された配列である:
アプリケーション (16)
写像と基底 (6)
Gram–Schmidt過程を適用して以下のベクトルから正規直交基底を構築する:
正規直交基底の最初のベクトル ![]() は単に正規化された倍数
は単に正規化された倍数 ![]() である:
である:
続くベクトルについては,前の基底ベクトルと平行な成分が正規化の前に引かれる:
Orthogonalizeを使って答を確かめる:
ベクトルによって形成された行列が非零の行列式を持つことを示すことで,これが基底であることを確認する:
Frenet–Serretの系は,ベクトル基底とスカラー関数におけるすべての空間曲線の特性を符号化する.以下の曲線について考える:
平行投影を減算することで,最初の3つの導関数から正規直交基底を構築する:
FrenetSerretSystemを使って答を確認する:
行列と線形演算子 (6)
OrthogonalMatrixQを使って確認する:
行列は ![]() のユニタリ行列である.Pauli行列がユニタリ行列であることを示す:
のユニタリ行列である.Pauli行列がユニタリ行列であることを示す:
UnitaryMatrixQで確認する:
![]() であれば行列は正規行列である.次の行列が正規行列であることを示す:
であれば行列は正規行列である.次の行列が正規行列であることを示す:
NormalMatrixQを使って確認する:
正規行列はその他の多くのタイプの行列を特殊ケースとして含む.ユニタリ行列は正規行列である:
![]() であるエルミート(Hermite)行列(自己随伴行列とも呼ばれる)もまた,行列
であるエルミート(Hermite)行列(自己随伴行列とも呼ばれる)もまた,行列 ![]() が示すように,正規行列である:
が示すように,正規行列である:
しかし,行列 ![]() はユニタリ行列やエルミート行列のように名前が付いた正規行列ではない:
はユニタリ行列やエルミート行列のように名前が付いた正規行列ではない:
量子力学では,有限個の状態を持つ系は単位ベクトルで,物理量はそれに作用する行列で表される.電子のようなスピン1/2の粒子について考える.この状態は以下のようなものかもしれない:
Dotで ![]() を使う方が速い:
を使う方が速い:
行列と対称性がある配列 (4)
正定値であることは関連付けられた二次形式 ![]() が
が ![]() について正であることを意味する:
について正であることを意味する:
Dot自体が恒等行列に関連付けられた内積である点に注意のこと:
Gram–Schmidt過程を標準基底に適用して正規直交基底を得る:
しかし,この形式は非縮退である.つまり,![]() は
は ![]() ということになる:
ということになる:
LeviCivitaTensorを使って完全に反対称な配列を六次元で構築する:
特性と関係 (16)
Dotの各引数は線形である:
実数項を持つベクトル ![]() について,Norm[v]は
について,Norm[v]は![]() に等しい:
に等しい:
実数項を持つ2つのベクトルについて ![]() ,ただし,
,ただし,![]() は
は ![]() と
と ![]() の間の角である:
の間の角である:
2つの行列について, ![]() の
の ![]() 番目と
番目と ![]()
![]() 番目の項は
番目の項は ![]() の
の ![]() 番目の行と
番目の行と ![]() の
の ![]()
![]() 番目の列のドット積である:
番目の列のドット積である:
MatrixPowerを使って繰返し行列の積を計算する:
ベクトルに対するbの動作はそのベクトルにaで4回動作することに等しい:
Dotを ![]() 階と
階と ![]() 階のテンソルに適用すると
階のテンソルに適用すると ![]() 階のテンソルが与えられる:
階のテンソルが与えられる:
Dotは配列の標準内積を実装する:
Timesを使って要素ごとの乗算を行う:
DotはTensorProductとTensorContractの組合せとして実装できる:
DotをFlattenと組み合せて使ってある配列の複数のレベルを別の配列の複数のレベルで縮約する:
TensorReduceはDotを含む式が簡約できる:
行行列と列行列のDotは対応するベクトルのKroneckerProductに等しい:
関連項目
MatrixPower Cross Norm KroneckerProduct Inner Outer Times Div TensorContract TensorProduct AffineTransform NonCommutativeMultiply VectorAngle Covariance LinearLayer DotLayer
Function Repository: FromTensor
テクニカルノート
-
▪
- ベクトルと行列 ▪
- ベクトルおよび行列の積
関連するガイド
-
▪
- 行列の操作 ▪
- GPU計算 ▪
- テンソル ▪
- ベクトル操作 ▪
- 行列と線形代数 ▪
- 記号的なベクトル,行列,配列 ▪
- 有限数学 ▪
- NVIDIAを使ったGPU計算 ▪
- リストへの数学的およびカウント操作 ▪
- 有限体 ▪
- 構造化配列 ▪
- グラフプログラミング
履歴
1988 で導入 (1.0) | 2003 で更新 (5.0) ▪ 2012 (9.0) ▪ 2024 (14.0)
テキスト
Wolfram Research (1988), Dot, Wolfram言語関数, https://reference.wolfram.com/language/ref/Dot.html (2024年に更新).
CMS
Wolfram Language. 1988. "Dot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Dot.html.
APA
Wolfram Language. (1988). Dot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Dot.html
BibTeX
@misc{reference.wolfram_2025_dot, author="Wolfram Research", title="{Dot}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Dot.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_dot, organization={Wolfram Research}, title={Dot}, year={2024}, url={https://reference.wolfram.com/language/ref/Dot.html}, note=[Accessed: 03-March-2026]}