Dot  ✖
✖
Dot
更多信息

- a 和 b 是适当维数的列表时,a.b 给出一个明确的结果. 它将 a 中最后一个指标与 b 中第一个指标之间建立约定.
- Dot 的各种应用:
-
{a1,a2}.{b1,b2} 向量的标积 {a1,a2}.{{m11,m12},{m21,m22}}向量和矩阵的乘积 {{m11,m12},{m21,m22}}.{a1,a2}矩阵和向量的乘积 {{m11,m12},{m21,m22}}.{{n11,n12},{n21,n22}}两个矩阵的乘积 - 对两个张量
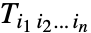 和
和 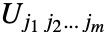 使用 Dot 的结果是张量
使用 Dot 的结果是张量 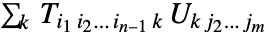 将 Dot 应用到一个
将 Dot 应用到一个 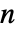 维张量和一个
维张量和一个 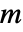 维张量得到一个
维张量得到一个 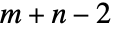 维的张量. »
维的张量. » - 可将 Dot 应用于 SparseArray 和结构化数组对象. 可能的情况下,它将返回与输入相同类型的对象. »
- 对于所有参数,Dot 都是线性的. » 它没有定义向量上的复(厄米特)内积. »
- 当它的参数不是列表或稀疏数组时,Dot 保持不计算. 它具有 Flat 属性.
范例
打开所有单元关闭所有单元基本范例 (4)常见实例总结
https://wolfram.com/xid/02cqd-2nv5gr
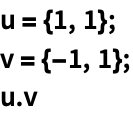
https://wolfram.com/xid/02cqd-rlu7fj
https://wolfram.com/xid/02cqd-peqyxh
https://wolfram.com/xid/02cqd-bg8lym
https://wolfram.com/xid/02cqd-nsnlin
https://wolfram.com/xid/02cqd-k0jn1c
https://wolfram.com/xid/02cqd-k7usjd
https://wolfram.com/xid/02cqd-wr3wn2
https://wolfram.com/xid/02cqd-o3l7ps
https://wolfram.com/xid/02cqd-wc5jg0
范围 (28)标准用法实例范围调查
向量的点积 (7)
https://wolfram.com/xid/02cqd-n9078n
https://wolfram.com/xid/02cqd-f1hujw
https://wolfram.com/xid/02cqd-z3441e
https://wolfram.com/xid/02cqd-vd7co8
https://wolfram.com/xid/02cqd-ex91be
Dot 允许复数输入,但不会取任意一个输入的共轭:
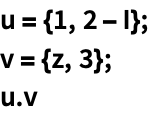
https://wolfram.com/xid/02cqd-cbz27c
如果想对复数或 Hermitian 内积进行计算,对其中一个输入应用 Conjugate:
https://wolfram.com/xid/02cqd-5l0ran
https://wolfram.com/xid/02cqd-we0c9i
https://wolfram.com/xid/02cqd-8z82wm
https://wolfram.com/xid/02cqd-3kxpp2
https://wolfram.com/xid/02cqd-z6nb90
用 Norm 验证结果:
https://wolfram.com/xid/02cqd-xw32ni
https://wolfram.com/xid/02cqd-q4hgd0
https://wolfram.com/xid/02cqd-3p06hh
https://wolfram.com/xid/02cqd-0co8u4
计算两个 QuantityArray 向量的标量积:
https://wolfram.com/xid/02cqd-80mcz5
https://wolfram.com/xid/02cqd-2zcedv
https://wolfram.com/xid/02cqd-l73cyi
矩阵-向量相乘 (5)
https://wolfram.com/xid/02cqd-3ype6l

https://wolfram.com/xid/02cqd-gd6rwr
https://wolfram.com/xid/02cqd-5xj0qn
https://wolfram.com/xid/02cqd-z97q8n
https://wolfram.com/xid/02cqd-45f19c
https://wolfram.com/xid/02cqd-j74d7f
https://wolfram.com/xid/02cqd-vm2lml
https://wolfram.com/xid/02cqd-ywj5u0
https://wolfram.com/xid/02cqd-orb8qb
https://wolfram.com/xid/02cqd-y3pyr7
定义一个列矩阵和一个行矩阵 c 和 r,其中的元素与 v 一样:
https://wolfram.com/xid/02cqd-1osa10
涉及 m、c 和 r 的乘积与涉及 m 和 v 的乘积的元素一样,但都是矩阵:
https://wolfram.com/xid/02cqd-ft19ie
https://wolfram.com/xid/02cqd-40nloq
https://wolfram.com/xid/02cqd-73tfw2
https://wolfram.com/xid/02cqd-62ivtp

https://wolfram.com/xid/02cqd-ntf53u
https://wolfram.com/xid/02cqd-uzt0t
https://wolfram.com/xid/02cqd-g3i4bh
https://wolfram.com/xid/02cqd-c3xmxn
https://wolfram.com/xid/02cqd-6e0cns
https://wolfram.com/xid/02cqd-6rawkm
https://wolfram.com/xid/02cqd-o4am55
https://wolfram.com/xid/02cqd-mip78l
https://wolfram.com/xid/02cqd-693yp2
https://wolfram.com/xid/02cqd-er7lsf
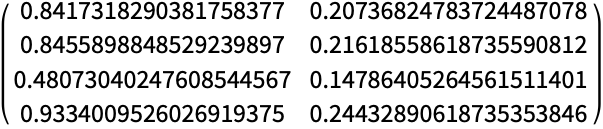
矩阵-矩阵相乘 (11)
https://wolfram.com/xid/02cqd-ncz1mo

https://wolfram.com/xid/02cqd-irmssc
https://wolfram.com/xid/02cqd-blxy1e
https://wolfram.com/xid/02cqd-hemkzc
https://wolfram.com/xid/02cqd-c373x7

https://wolfram.com/xid/02cqd-b1j1sz
https://wolfram.com/xid/02cqd-tr4f1


https://wolfram.com/xid/02cqd-pww6q
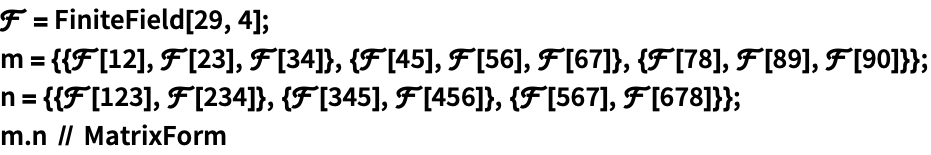
https://wolfram.com/xid/02cqd-nw2qll

CenteredInterval 矩阵的乘积:
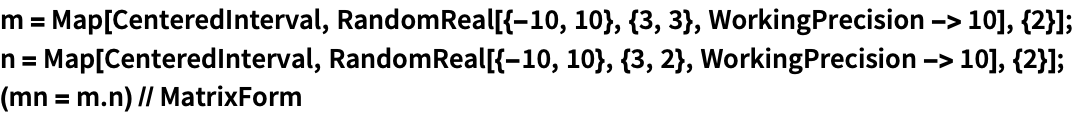
https://wolfram.com/xid/02cqd-ghxly8

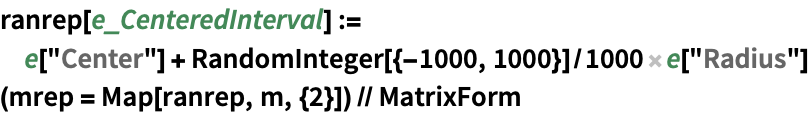
https://wolfram.com/xid/02cqd-b7u4hh

https://wolfram.com/xid/02cqd-fq7fj1

https://wolfram.com/xid/02cqd-27bmd

https://wolfram.com/xid/02cqd-lhfeiq
https://wolfram.com/xid/02cqd-m6qbwl

https://wolfram.com/xid/02cqd-n4lvad
https://wolfram.com/xid/02cqd-upvhcj
https://wolfram.com/xid/02cqd-wajwti
https://wolfram.com/xid/02cqd-ylu6mb
与 MatrixPower 的结果相比较:
https://wolfram.com/xid/02cqd-6z66qk
用 Dot 与 Apply (@@) 和 ConstantArray 计算矩阵的 10 次方:
https://wolfram.com/xid/02cqd-rfip7d
https://wolfram.com/xid/02cqd-mbdoyo

https://wolfram.com/xid/02cqd-3sijcl
高阶数组 (5)
Dot 适用于任意阶数的数组:

https://wolfram.com/xid/02cqd-0npemv
https://wolfram.com/xid/02cqd-oprsnp

https://wolfram.com/xid/02cqd-bct7q
https://wolfram.com/xid/02cqd-vt925v
https://wolfram.com/xid/02cqd-ikt229
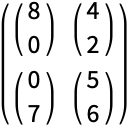
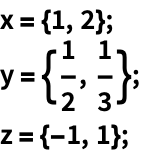
https://wolfram.com/xid/02cqd-jgghlw
![]() 是完全缩并
是完全缩并 ![]() ,将
,将 ![]() 与
与 ![]() 的最后一层相配,将
的最后一层相配,将 ![]() 与
与 ![]() 的第一层相配:
的第一层相配:
https://wolfram.com/xid/02cqd-1kn30q
![]() 是不同的缩并
是不同的缩并 ![]() ,将
,将 ![]() 与
与 ![]() 的第一层相配,将
的第一层相配,将 ![]() 与
与 ![]() 的最后一层相配:
的最后一层相配:
https://wolfram.com/xid/02cqd-mbp8jt

https://wolfram.com/xid/02cqd-lp4nvs
两个稀疏数组的 Dot 通常是另一个稀疏数组:
https://wolfram.com/xid/02cqd-jhf21p
https://wolfram.com/xid/02cqd-27lx98
https://wolfram.com/xid/02cqd-u6ay98
一个稀疏数组与一个普通列表的 Dot 可能是另一个稀疏数组或普通列表:
https://wolfram.com/xid/02cqd-brwhqh
https://wolfram.com/xid/02cqd-jcdaky
https://wolfram.com/xid/02cqd-baqyqn
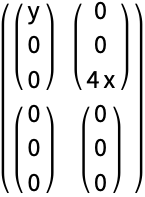
两个 SymmetrizedArray 对象的乘积通常是另一个对称数组:

https://wolfram.com/xid/02cqd-k6p7gt

https://wolfram.com/xid/02cqd-takcdo
https://wolfram.com/xid/02cqd-k0bsdz
应用 (16)用该函数可以解决的问题范例
投影和基 (6)
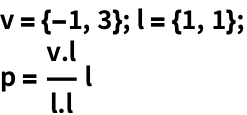
https://wolfram.com/xid/02cqd-1rf22h

https://wolfram.com/xid/02cqd-bb5qc5
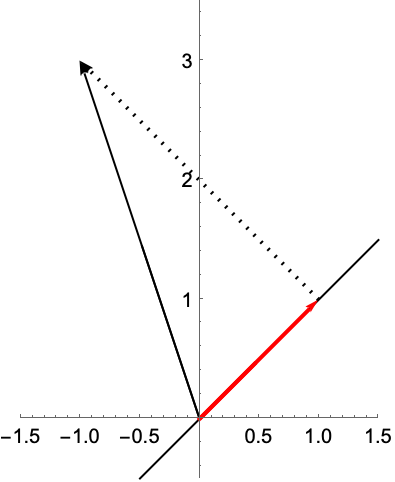
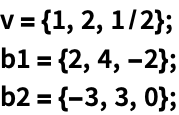
https://wolfram.com/xid/02cqd-t5aqq0
https://wolfram.com/xid/02cqd-556932
https://wolfram.com/xid/02cqd-6sqj73
https://wolfram.com/xid/02cqd-vy5nk0
https://wolfram.com/xid/02cqd-usowgy

https://wolfram.com/xid/02cqd-l0ji89
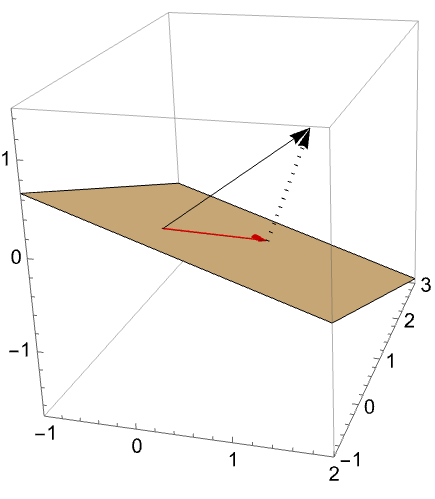
应用 Gram–Schmidt 过程根据以下向量构建正交基:
https://wolfram.com/xid/02cqd-ipdyf1
https://wolfram.com/xid/02cqd-trym6a
https://wolfram.com/xid/02cqd-ez7k6a
https://wolfram.com/xid/02cqd-4zt373
https://wolfram.com/xid/02cqd-4wc2on
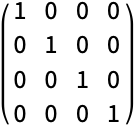
用 Orthogonalize 确认答案:
https://wolfram.com/xid/02cqd-s42jvt
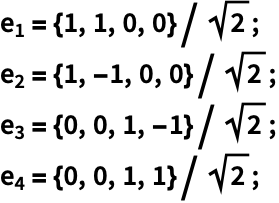
https://wolfram.com/xid/02cqd-mgqdax
https://wolfram.com/xid/02cqd-w5gmoi
https://wolfram.com/xid/02cqd-20j6cc
https://wolfram.com/xid/02cqd-ijqswp
https://wolfram.com/xid/02cqd-34ypwx
https://wolfram.com/xid/02cqd-svkrze
https://wolfram.com/xid/02cqd-ie0q9c
https://wolfram.com/xid/02cqd-44tmnt
https://wolfram.com/xid/02cqd-p3suks
https://wolfram.com/xid/02cqd-kk9uuy
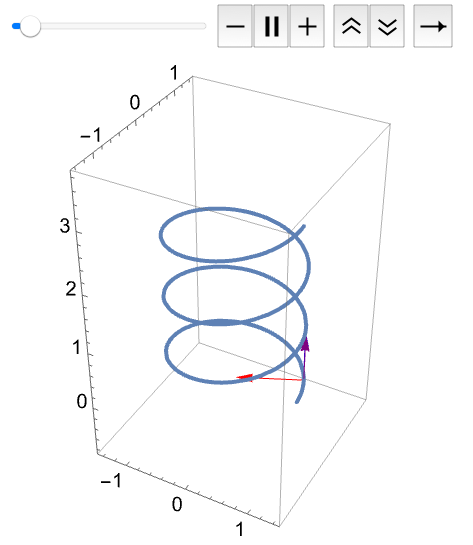
Frenet–Serret 系统将每条空间曲线的属性编码到向量基和标量函数中. 考虑以下曲线:
https://wolfram.com/xid/02cqd-rw3aai
https://wolfram.com/xid/02cqd-bmpr4j
https://wolfram.com/xid/02cqd-dly7ni
https://wolfram.com/xid/02cqd-mufwwo
用 FrenetSerretSystem 验证答案:
https://wolfram.com/xid/02cqd-k6so6w

https://wolfram.com/xid/02cqd-eumwkl
矩阵和线性算子 (6)
https://wolfram.com/xid/02cqd-rl81a3
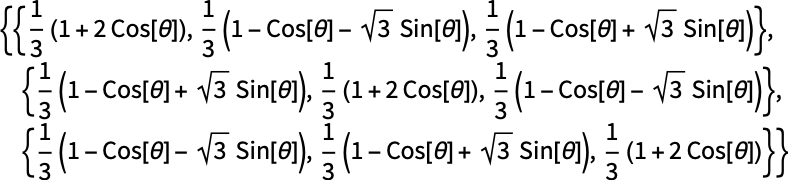
https://wolfram.com/xid/02cqd-zgnm3n
用 OrthogonalMatrixQ 确认:
https://wolfram.com/xid/02cqd-bu72ly
https://wolfram.com/xid/02cqd-usqzs3
https://wolfram.com/xid/02cqd-0e24pu
用 UnitaryMatrixQ 确认:
https://wolfram.com/xid/02cqd-cs5hfw
https://wolfram.com/xid/02cqd-usjbn0
用 NormalMatrixQ 确认:
https://wolfram.com/xid/02cqd-8ernzh
正规矩阵包括许多其他类型的矩阵,为正规矩阵的特例. 酉矩阵是正规矩阵:
https://wolfram.com/xid/02cqd-szmdf0
https://wolfram.com/xid/02cqd-yw4cka
https://wolfram.com/xid/02cqd-vyprzo
在量子力学中,具有有限多个状态的系统由单位向量表示,物理量由作用于它们的矩阵表示. 考虑一个自旋 1/2 的粒子,如电子. 它可能处于如下状态:
https://wolfram.com/xid/02cqd-38x16q
https://wolfram.com/xid/02cqd-sja8mn
https://wolfram.com/xid/02cqd-3srgxm
https://wolfram.com/xid/02cqd-xtk4yx
https://wolfram.com/xid/02cqd-l30enu
https://wolfram.com/xid/02cqd-9r9je9
https://wolfram.com/xid/02cqd-kcsb44
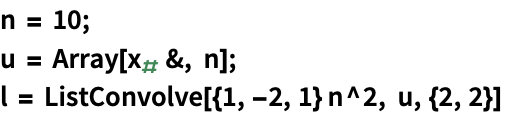
https://wolfram.com/xid/02cqd-cid5sq
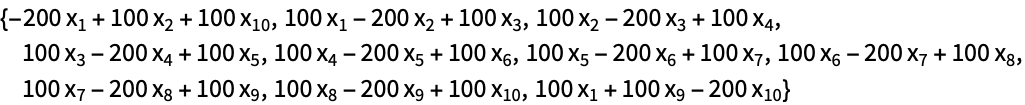
https://wolfram.com/xid/02cqd-0w233f
https://wolfram.com/xid/02cqd-z0iti
https://wolfram.com/xid/02cqd-pycqoz
https://wolfram.com/xid/02cqd-etzj5l
https://wolfram.com/xid/02cqd-hh8zny
将 ![]() 与 Dot 一起使用是最快的方法:
与 Dot 一起使用是最快的方法:

https://wolfram.com/xid/02cqd-iufy0n
https://wolfram.com/xid/02cqd-5vwze0
https://wolfram.com/xid/02cqd-2y6rrz
https://wolfram.com/xid/02cqd-kagdsr
https://wolfram.com/xid/02cqd-emcqm4
https://wolfram.com/xid/02cqd-gvoadx
具有对称性的矩阵和数组 (4)
https://wolfram.com/xid/02cqd-9qtx6s
https://wolfram.com/xid/02cqd-5b73fr
https://wolfram.com/xid/02cqd-oj4kij
https://wolfram.com/xid/02cqd-lqoxhq
https://wolfram.com/xid/02cqd-0baxmq
https://wolfram.com/xid/02cqd-ycw1jx
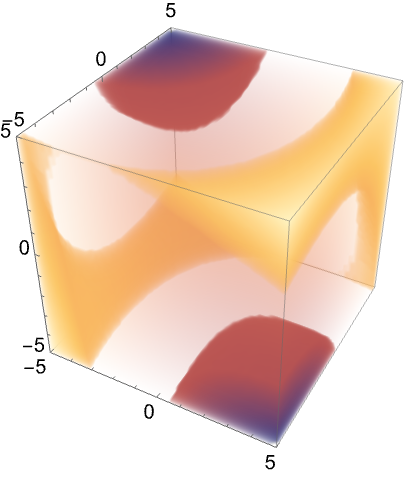
https://wolfram.com/xid/02cqd-xs2xkr
https://wolfram.com/xid/02cqd-i29f9p
https://wolfram.com/xid/02cqd-f5yka3
注意 Dot 本身是与单位矩阵相关的内积:
https://wolfram.com/xid/02cqd-vw5ltx
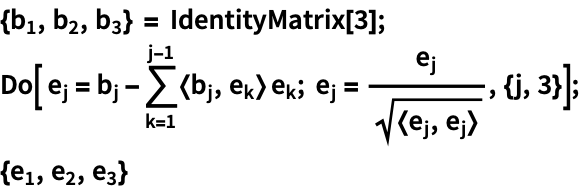
https://wolfram.com/xid/02cqd-9jtyba
https://wolfram.com/xid/02cqd-mkuz95
对于反对称矩阵 ![]() ,
,![]() 定义了一个 Hamiltonian 2-form
定义了一个 Hamiltonian 2-form ![]() :
:
https://wolfram.com/xid/02cqd-uvb16x

https://wolfram.com/xid/02cqd-k7tr9y
https://wolfram.com/xid/02cqd-ifqtyk
https://wolfram.com/xid/02cqd-riu0jg
https://wolfram.com/xid/02cqd-5frid3
https://wolfram.com/xid/02cqd-pysujz

用 LeviCivitaTensor 构建六维全反对称数组:
https://wolfram.com/xid/02cqd-kzgi5b
https://wolfram.com/xid/02cqd-osemks
https://wolfram.com/xid/02cqd-qmh0co
根据 ![]() 的反对称,反向缩并 (reversed contraction) 的区别是维度
的反对称,反向缩并 (reversed contraction) 的区别是维度 ![]() 上相差
上相差 ![]() :
:
https://wolfram.com/xid/02cqd-dp57h3
属性和关系 (16)函数的属性及与其他函数的关联
对于每个参数,Dot 都是线性的:
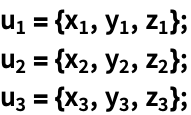
https://wolfram.com/xid/02cqd-e9q9ue
https://wolfram.com/xid/02cqd-ikv3n
https://wolfram.com/xid/02cqd-ci1a2f
对于实向量 ![]() ,Norm[v] 等于
,Norm[v] 等于 ![]() :
:
https://wolfram.com/xid/02cqd-oxfzh
https://wolfram.com/xid/02cqd-u32nko
https://wolfram.com/xid/02cqd-gdmvu6
https://wolfram.com/xid/02cqd-p16weh
https://wolfram.com/xid/02cqd-73nauh
https://wolfram.com/xid/02cqd-l1kkf8

https://wolfram.com/xid/02cqd-47cn13
对于两个矩阵,![]() 的第
的第 ![]() 和第
和第 ![]() 项是
项是 ![]() 的第
的第 ![]() 行与
行与 ![]() 的第
的第 ![]() 列的点积:
列的点积:
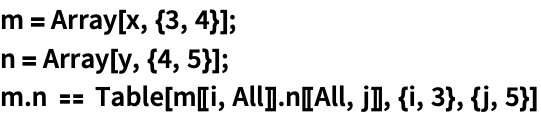
https://wolfram.com/xid/02cqd-i6f9x2

https://wolfram.com/xid/02cqd-f2bkec
用 MatrixPower 计算重复的矩阵相乘:
https://wolfram.com/xid/02cqd-h2otbd
https://wolfram.com/xid/02cqd-hhvw2b
https://wolfram.com/xid/02cqd-nu828k
https://wolfram.com/xid/02cqd-i6q0os

https://wolfram.com/xid/02cqd-39xbig
对秩为 ![]() 的张量和秩为
的张量和秩为 ![]() 的张量应用 Dot 给出秩为
的张量应用 Dot 给出秩为 ![]() 的张量:
的张量:
https://wolfram.com/xid/02cqd-u5lpym
https://wolfram.com/xid/02cqd-ihttlp
https://wolfram.com/xid/02cqd-f5e3x5
https://wolfram.com/xid/02cqd-8edu6d
Dot 实现了数组的标准内积:
https://wolfram.com/xid/02cqd-8ddd1p
使用 Times 做元素乘法:
https://wolfram.com/xid/02cqd-b36o97
可通过 TensorProduct 和 TensorContract 组合使用实现 Dot:
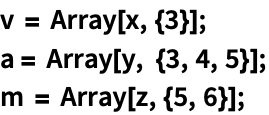
https://wolfram.com/xid/02cqd-ej1tta
https://wolfram.com/xid/02cqd-dzk5e5
将 Dot 与 Flatten 一起使用以缩并一个数组的多个层级与另一个数组的多个层级:
https://wolfram.com/xid/02cqd-e1xdmi
https://wolfram.com/xid/02cqd-fela60
TensorReduce 可简化含有 Dot 的表达式:
https://wolfram.com/xid/02cqd-8w0f4e
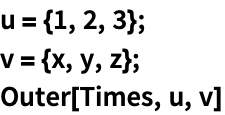
https://wolfram.com/xid/02cqd-y8vwui
https://wolfram.com/xid/02cqd-tbklq8
https://wolfram.com/xid/02cqd-ys573h
https://wolfram.com/xid/02cqd-li5n8b
一个行矩阵和列矩阵的 Dot 等于对应向量的 KroneckerProduct:

https://wolfram.com/xid/02cqd-2f9dxl
可能存在的问题 (2)常见隐患和异常行为
Dot 实际上从右边处理多维向量,可以视为列向量:
https://wolfram.com/xid/02cqd-blgtoq
https://wolfram.com/xid/02cqd-i6pdop
https://wolfram.com/xid/02cqd-ljimti
Dot 实际上从左边边处理多维向量,可以视为行向量:
https://wolfram.com/xid/02cqd-daadm
https://wolfram.com/xid/02cqd-kd327t
Dot 不给出 ![]() 的标准内积:
的标准内积:
https://wolfram.com/xid/02cqd-mhb61v
https://wolfram.com/xid/02cqd-josa09
对一个参数应用 Conjugate 以获取厄米特内积:
https://wolfram.com/xid/02cqd-m58fbd
https://wolfram.com/xid/02cqd-pxgh3h
Wolfram Research (1988),Dot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Dot.html (更新于 2024 年).文本
Wolfram Research (1988),Dot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Dot.html (更新于 2024 年).
Wolfram Research (1988),Dot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Dot.html (更新于 2024 年).CMS
Wolfram 语言. 1988. "Dot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Dot.html.
Wolfram 语言. 1988. "Dot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Dot.html.APA
Wolfram 语言. (1988). Dot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Dot.html 年
Wolfram 语言. (1988). Dot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Dot.html 年BibTeX
@misc{reference.wolfram_2025_dot, author="Wolfram Research", title="{Dot}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Dot.html}", note=[Accessed: 04-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_dot, organization={Wolfram Research}, title={Dot}, year={2024}, url={https://reference.wolfram.com/language/ref/Dot.html}, note=[Accessed: 04-April-2025
]}