尺度が母数 λ に反比例する指数分布を表す.


ExponentialDistribution
尺度が母数 λ に反比例する指数分布を表す.
詳細
- 指数分布における値
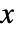 の確率密度は,
の確率密度は,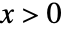 のときは
のときは 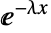 に比例し,
に比例し,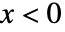 のときは0である. »
のときは0である. » - ExponentialDistributionでは,λ は任意の正の実数でよい.
- ExponentialDistributionでは,λ は任意の単位次元の数量でよい. »
- ExponentialDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- ExponentialDistribution[λ]は,区間
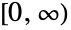 上で定義され,正の実数 λ でパラメータ化された連続統計分布を表す.指数分布の確率密度関数(PDF)は,単調減少である.これに加え,PDFの裾部は,PDFが
上で定義され,正の実数 λ でパラメータ化された連続統計分布を表す.指数分布の確率密度関数(PDF)は,単調減少である.これに加え,PDFの裾部は,PDFが 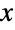 の大きい値について指数的に減少するという意味で「薄い」(この現象は,分布のSurvivalFunctionを分析することで数量的に正確にできる).指数分布は時に負の指数分布,1母数指数分布,あるいは反対数分布と呼ばれることがある.
の大きい値について指数的に減少するという意味で「薄い」(この現象は,分布のSurvivalFunctionを分析することで数量的に正確にできる).指数分布は時に負の指数分布,1母数指数分布,あるいは反対数分布と呼ばれることがある. - 歴史的に,指数分布は「時間的にランダム」におこる現象,つまり,個の未来の寿命が現在の状態に関係なく同じ分布に従う現象の説明のために幅広く使われてきた.指数分布の使用は,過去75年間に大幅に増大した.これは,一つには,1950年代の初頭から中頃にかけて始まった順序統計の分野で研究が盛んに行われたためである.それ以来指数分布は,ほぼ一定割合の区間内でのさまざまな現象,例えば一日の特定の時間帯にかかってくる電話の数のモデル化に使われてきた,確率過程では,指数分布は,同次ポアソン過程における到着間隔の長さ(つまり,増分が独立かつ定常でポアソン分布に従う,PoissonProcessとして実装されている連続時間計数過程)の説明に使われた.指数分布は,クレジットリスクのモデル化,待ち行列理論,信頼性理論,物理学,水文学にも使われている.
- RandomVariateを使って指数分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,ExponentialDistribution[λ]](より簡略すると xExponentialDistribution[λ])を使って,確率変数 x が,指数分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[ExponentialDistribution[λ],x]およびCDF[ExponentialDistribution[λ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が指数分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック指数分布を推定することが,FindDistributionParametersを使ってデータを指数分布にフィットすることができる.ProbabilityPlotを使って記号指数分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号指数分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された指数分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って指数分布を含む高次元分布を構築することが,ProductDistributionを使って指数分布を含む独立成分分布の結合分布を計算することができる.
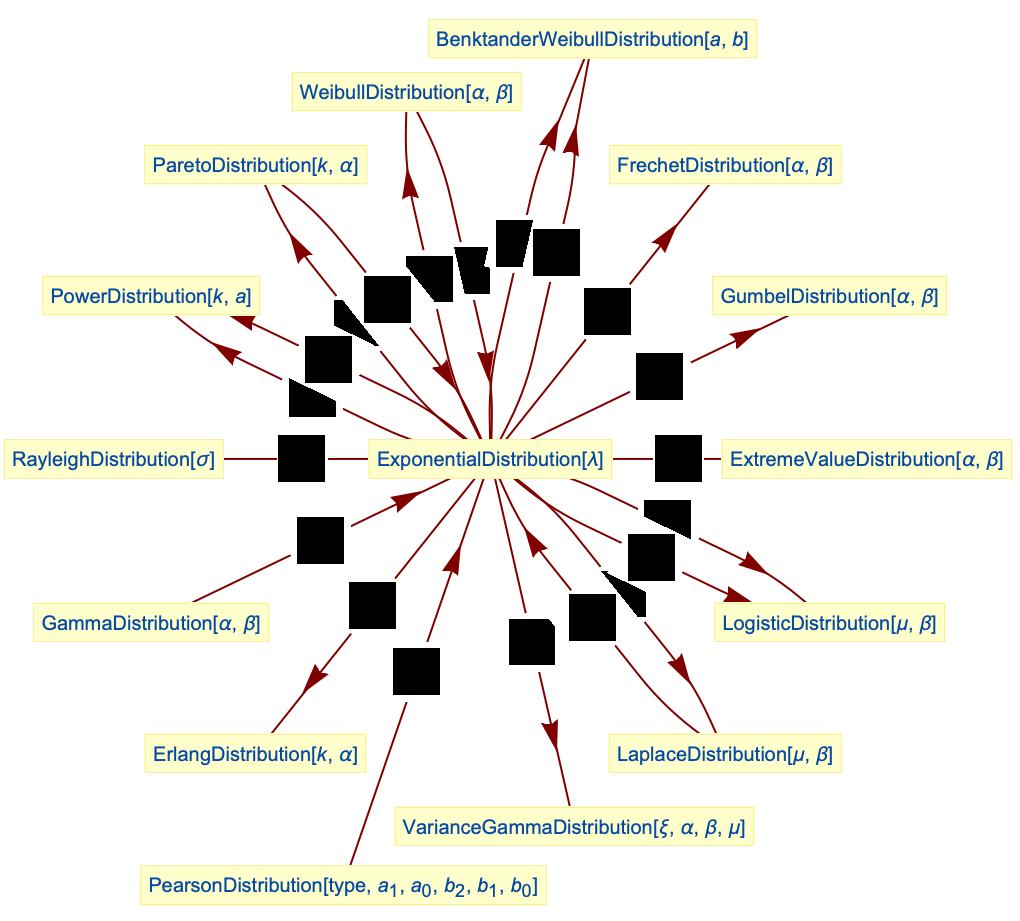
- 指数分布は他の多くの分布と関係している.この分布のPoissonProcessと相対的な発現は,PoissonDistributionおよびCompoundPoissonDistributionとの関係を考えさせる.ExponentialDistributionは,ExponentialDistribution[1]がExtremeValueDistribution,GumbelDistribution,FrechetDistribution,WeibullDistributionのそれぞれに変換でき,ExponentialDistributionがGammaDistribution,LaplaceDistribution,BenktanderWeibullDistribution,LogisticDistribution,ParetoDistribution,PearsonDistribution,PowerDistribution,RayleighDistributionのそれぞれからTransformedDistributionおよび/またはTruncatedDistributionによって得られることから,極値分布族の基礎であると考えることができる.ExponentialDistributionと他の分布を組み合せていくつかの分布を派生させることができる(例えばExponentialDistributionとPoissonDistributionを組み合せてGeometricDistribution,GammaDistributionと組合せてKDistribution,ArcSinDistributionと組み合せてHoytDistribution,ErlangDistributionまたはGammaDistributionと組み合せてParetoDistribution等).
例題
すべて開く すべて閉じるスコープ (7)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (9)
寿命が1時間あたり比率母数![]() の指数分布に従う電池がある.無作為抽出した電池の寿命が2500時間より短い確率を求める:
の指数分布に従う電池がある.無作為抽出した電池の寿命が2500時間より短い確率を求める:
寿命が故障率 ![]() /年の指数分布に従う継電器がある.製品保証の経費を見積るために,使用開始から6ヶ月の間に故障する継電器の数が10000の中でいくつあるかを推定する.故障率はハザード率としても知られている:
/年の指数分布に従う継電器がある.製品保証の経費を見積るために,使用開始から6ヶ月の間に故障する継電器の数が10000の中でいくつあるかを推定する.故障率はハザード率としても知られている:
10000個の継電器のうちで最初の6ヶ月間に予想される故障数:
故障までの時間が母数 ![]() の指数分布に従う製品がある.製品の信頼性を1年間,2年間,3年間について求める.信頼性とはSurvivalFunctionの別名である:
の指数分布に従う製品がある.製品の信頼性を1年間,2年間,3年間について求める.信頼性とはSurvivalFunctionの別名である:
ある電化製品の寿命が平均10年の指数分布に従うと仮定し,製品の寿命分布を求める:
使用年数が ![]() 年の中古の電化製品が次の5年間に故障しない確率を求める:
年の中古の電化製品が次の5年間に故障しない確率を求める:
ExponentialDistributionの無記憶性を使用する:
レストランの顧客の待ち時間が平均5分の指数分布に従うと仮定し,顧客が10分以上待たなければならない確率を求める:
すでに少なくとも10分待っている顧客がさらに10分待たなければならない確率を求める(過去は関係ない):
1902年12月16日から1977年3月4日までに世界で起った大地震(マグニチュードが最低7.5,あるいは死者が1000人以上)の発生間隔を日を単位として記録したデータがある:
ExponentialDistributionをデータにフィットする:
今後世界中で起る30の大地震について,地震と地震の間の日数のシミュレーションを行う:
4つの独立した送信機からの信号を待つ受信機側の待ち時間は母数をそれぞれ ![]() ,
,![]() ,
,![]() ,
,![]() として指数分布に従っている.3番目の送信機からの信号が最初に受信機に届く確率を求める:
として指数分布に従っている.3番目の送信機からの信号が最初に受信機に届く確率を求める:
1つの信号から次の信号までの受信機の待ち時間を ![]() ,
,![]() ,
,![]() ,
,![]() についてそれぞれシミュレーションする:
についてそれぞれシミュレーションする:
寿命が母数![]() /時の指数分布に従う4つの独立した部品からなるシステムがある.500時間経過するまでどの部品も故障しない確率を求める:
/時の指数分布に従う4つの独立した部品からなるシステムがある.500時間経過するまでどの部品も故障しない確率を求める:
SurvivalFunctionを直接使う:
最初の1200時間で厳密に1つの部品が故障する確率を求める:
CDFとSurvivalFunctionを直接使う:
BooleanCountingFunctionを使うと論理条件も定義できる:
光通信システムでは,透過光は受信機で電流を生成する.電子の数は光のタイプによりポアソン分布と他の分布のパラメトリック混合分布に従う.光源に強度 λ のコヒーレントレーザー光線を使う場合,電子の数はポアソン分布に従う:
光源に熱照明を使う場合,ポアソン母数は母数![]() のExponentialDistributionに従い,電子数の分布は以下のようになる:
のExponentialDistributionに従い,電子数の分布は以下のようになる:
特性と関係 (31)
BenktanderWeibullDistributionを簡約すると切断ExponentialDistributionになる:
シフトされたExponentialDistributionはBenktanderWeibullDistributionである:
指数分布はスケールされたBetaDistributionの極限である:
PowerDistributionは指数分布の変換である:
指数分布はPowerDistributionから得ることができる:
指数分布はBetaDistributionから得ることができる:
独立指数分布に従う確率変数の総和はErlangDistributionに従う:
ExponentialDistribution[1]は極値分布族に変換することができる:
ExponentialDistributionはWeibullDistributionの特殊ケースである:
ExponentialDistributionはGammaDistributionの特殊ケースである:
同じ指数分布に従う2変量の差はLaplaceDistributionに従う:
2つの異なる指数分布の差はVarianceGammaDistributionに従う:
指数分布はLaplaceDistributionを変換したものである:
LogisticDistributionは指数分布から変換したものである:
LogisticDistributionは指数分布を変換したものである:
ParetoDistributionは指数分布を変換したものである:
ParetoDistributionの変換は指数分布を与える:
指数分布はタイプ3のPearsonDistributionの特殊ケースである:
PowerDistributionは指数分布を変換したものである:
指数分布はRayleighDistributionから得ることができる:
指数分布は ![]() の極限分布である.ただし,
の極限分布である.ただし,![]() はUniformDistributionに従うものとする:
はUniformDistributionに従うものとする:
PoissonDistributionと指数分布のパラメトリック混合分布はGeometricDistributionに従う:
KDistributionはExponentialDistributionとGammaDistributionから得ることができる:
HoytDistributionはExponentialDistributionとArcSinDistributionから得ることができる:
ParetoDistributionはExponentialDistributionとErlangDistributionの商として求められる:
ParetoDistributionはExponentialDistributionとGammaDistributionの商として求められる:
考えられる問題 (2)
テクニカルノート
-
▪
- 連続分布
関連するガイド
-
▪
- 指数関連分布 ▪
- 待ち行列過程 ▪
- 信頼性解析の分布 ▪
- 信頼性解析 ▪
- 保険数理で使われる分布 ▪
- 保険数理計算 ▪
- パラメトリック統計分布 ▪
- 生存率分析 ▪
- 通信システムの分布 ▪
- 確率・統計における数量
テキスト
Wolfram Research (2007), ExponentialDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/ExponentialDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "ExponentialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ExponentialDistribution.html.
APA
Wolfram Language. (2007). ExponentialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExponentialDistribution.html
BibTeX
@misc{reference.wolfram_2025_exponentialdistribution, author="Wolfram Research", title="{ExponentialDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ExponentialDistribution.html}", note=[Accessed: 16-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_exponentialdistribution, organization={Wolfram Research}, title={ExponentialDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ExponentialDistribution.html}, note=[Accessed: 16-February-2026]}