GeometricDistribution
確率母数が p の幾何分布を表す.
詳細
- 幾何分布における値
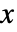 の確率は,非負の整数については
の確率は,非負の整数については 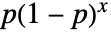 であり,その他の場合はゼロである. »
であり,その他の場合はゼロである. » - GeometricDistribution[p]は,成功確率が p の一連の試行における成功までの失敗回数の分布である.
- GeometricDistributionでは,p は無次元量でよい. »
- GeometricDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- GeometricDistribution[p]は,整数値
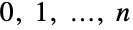 で定義され,非負の実数
で定義され,非負の実数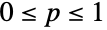 でパラメータ化された離散統計分布を表す.幾何分布は,単調減少の離散確率密度関数(PDF)を持つ.母数 p がPDFの高さと傾きを決定する.幾何分布はFurry分布と呼ばれることがある.
でパラメータ化された離散統計分布を表す.幾何分布は,単調減少の離散確率密度関数(PDF)を持つ.母数 p がPDFの高さと傾きを決定する.幾何分布はFurry分布と呼ばれることがある. - 幾何分布は,指数分布(ExponentialDistribution)の離散バージョンであると言われることがある.これは,1回成功するために必要なベルヌーイ試行の回数(つまり,BernoulliDistributionに従う変量の試行回数)をモデル化する分布として定義することができる. 幾何分布は,競合植物群の性質,チケット制御の力学,先天性奇形の詳細,動物の個体数の推定等を含む,さまざまな分野の数多くの現象のモデル化に使われてきた.さらに,幾何分布は信頼性理論で広く使われ,気象学,待ち行列理論,応用確率論におけるマルコフ鎖モデルに必須となっている.
- RandomVariateを使って,幾何分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,GeometricDistribution[p]](より簡略すると xGeometricDistribution[p])を使って,確率変数 x が,幾何分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[GeometricDistribution[p],x]およびCDF[GeometricDistribution[p],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合が幾何分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック幾何分布を推定することが,FindDistributionParametersを使ってデータを幾何分布にフィットすることができる.ProbabilityPlotを使って記号幾何分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号幾何分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された幾何分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って幾何分布を含む高次元分布を構築することが,ProductDistributionを使って幾何分布を含む独立成分分布の結合分布を計算することができる.
- GeometricDistributionは他の多くの統計分布と関連している.例えば,GeometricDistributionは,NegativeBinomialDistribution[1,p]がGeometricDistribution[p]と厳密に同じPDFを持ち,
 の和が,すべての
の和が,すべての  について XiGeometricDistribution[p]であるという条件の下でNegativeBinomialDistribution[n,p]に従って分布しているという意味で,より一般的なNegativeBinomialDistributionの特殊ケースである.GeometricDistributionはPascalDistributionの変換でもあり,ParameterMixtureDistribution[PoissonDistribution[μ],μGammaDistribution[1,(1-p)/p]]およびParameterMixtureDistribution[PoissonDistribution[μ],μ ExponentialDistribution[p/(1-p)]]の両方が,GeometricDistribution[p]と等しいという意味で,PoissonDistributionとGammaDistributionあるいはExponentialDistributionとの母数混合分布と考えることができる.GeometricDistributionはWaringYuleDistribution,BinomialDistribution,PascalDistribution,HypergeometricDistributionとも関連している.
について XiGeometricDistribution[p]であるという条件の下でNegativeBinomialDistribution[n,p]に従って分布しているという意味で,より一般的なNegativeBinomialDistributionの特殊ケースである.GeometricDistributionはPascalDistributionの変換でもあり,ParameterMixtureDistribution[PoissonDistribution[μ],μGammaDistribution[1,(1-p)/p]]およびParameterMixtureDistribution[PoissonDistribution[μ],μ ExponentialDistribution[p/(1-p)]]の両方が,GeometricDistribution[p]と等しいという意味で,PoissonDistributionとGammaDistributionあるいはExponentialDistributionとの母数混合分布と考えることができる.GeometricDistributionはWaringYuleDistribution,BinomialDistribution,PascalDistribution,HypergeometricDistributionとも関連している.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
無次元のQuantityを使ってGeometricDistributionを定義する:
アプリケーション (11)
GeometricDistributionのCDFは右連続関数の例である:
公正なコインを裏が出るまで繰り返しはじくコイントスの実験を行う.このプロセスのシミュレーションを行う:
道端に立って車を数えている男がいる.男は赤い車が来るとまた1から数え始める.車の20%が赤であると仮定して計数過程のシミュレーションを行う:
ある学生が合格するまで試験を受け続けるとする.各回の成功確率を p としてこの学生が ![]() 回以下の受験回数で合格する確率を求める:
回以下の受験回数で合格する確率を求める:
この学生が ![]() 回以下の受験で合格するとして確率密度関数を求める:
回以下の受験で合格するとして確率密度関数を求める:
火が付く確率が90%の安価なライターがある.着火プロセスのシミュレーションを行う.結果は着火に成功するまでの失敗回数を示す:
一箱に ![]() 種類のプラスティック製動物模型のどれか1つが入っているシリアルがある.動物模型は他の箱にどの動物が入っているかに関係なくどれも同じ割合で入っている.25箱買えば10種類の動物が集まると仮定してコレクション過程のシミュレーションを行う:
種類のプラスティック製動物模型のどれか1つが入っているシリアルがある.動物模型は他の箱にどの動物が入っているかに関係なくどれも同じ割合で入っている.25箱買えば10種類の動物が集まると仮定してコレクション過程のシミュレーションを行う:
![]() 個の別種の動物模型を集めた後で,
個の別種の動物模型を集めた後で,![]() 種類のまだ集めていない模型のいずれかを得るために必要な箱の数は,母数
種類のまだ集めていない模型のいずれかを得るために必要な箱の数は,母数![]() の幾何分布に従う.まだ集めていない動物模型のいずれかを得るのに必要と予想される箱の数を求める:
の幾何分布に従う.まだ集めていない動物模型のいずれかを得るのに必要と予想される箱の数を求める:
コンピュータがメモリにアクセスする際,所望のデータは p の確率でキャッシュされている.所望のデータがキャッシュされていない場合はキャッシュエラーが起る.![]()
![]() 回目のメモリアクセスでキャッシュエラーが起る確率を求める:
回目のメモリアクセスでキャッシュエラーが起る確率を求める:
4回のメモリアクセスの後にはじめてキャッシュエラーが起る確率を求める:
最初のキャッシュエラーが起るまでのメモリアクセスの平均回数を求める:
データの20%がキャッシュされていると仮定して,キャッシュエラーが起るまでのキャッシュのヒット数のシミュレーションを行う:
アクセス時間はキャッシュに対してが10ナノ秒,RAMに対してが1000ナノ秒と仮定して,平均アクセス時間を求める:
![]() 個のデータパケットを含むデータストリームが順序の情報なしに繰り返し送られている.最初にすべてのパケットが正しい順序で届くまでの試行回数の分布を求める:
個のデータパケットを含むデータストリームが順序の情報なしに繰り返し送られている.最初にすべてのパケットが正しい順序で届くまでの試行回数の分布を求める:
パケットが正しい順序で届くまでの試行回数が20回以下である確率を求める:
データストリームが正しい順序ではじめて送られるまでの試行回数のシミュレーションを行う:
データストリームがはじめて正しい順序で届くまでの試行回数の平均を求める:
賭け金の上限なしのカジノで勝率 ![]() のゲームに
のゲームに ![]() 賭けた人がいる.この人は負けると賭け金を2倍にし,勝った場合は賭けを止める.ゆえに,賭けたゲーム数は幾何分布に従い,賭けたゲームの期待値は次の通りになる:
賭けた人がいる.この人は負けると賭け金を2倍にし,勝った場合は賭けを止める.ゆえに,賭けたゲーム数は幾何分布に従い,賭けたゲームの期待値は次の通りになる:
上記の作戦でゲームを行うために準備が必要な現金は厳密に有利なゲームについてのみ有限で,その場合は![]() である:
である:
光通信システムでは,送信された光が受信器で電流を生成する.電子数は光の種類によってポアソン(Poisson)分布と他の分布の母数混合分布に従う.ソースで強度 ![]() の可干渉性レーザー光が使われているのであれば,電子数はポアソン分布に従う:
の可干渉性レーザー光が使われているのであれば,電子数はポアソン分布に従う:
これはPoissonDistributionである:
ソースで熱照明が使われているのなら,ポアソン母数は母数が![]() のExponentialDistributionに従い,電子数の分布は以下のようになる:
のExponentialDistributionに従い,電子数の分布は以下のようになる:
これら2つの分布は識別可能で,ソースタイプの判断を可能とする:
p についてのモーメント法推定器のサンプリング母集団推定を求める:
特性と関係 (8)
GeometricDistributionの族はMinのもとでは閉じている:
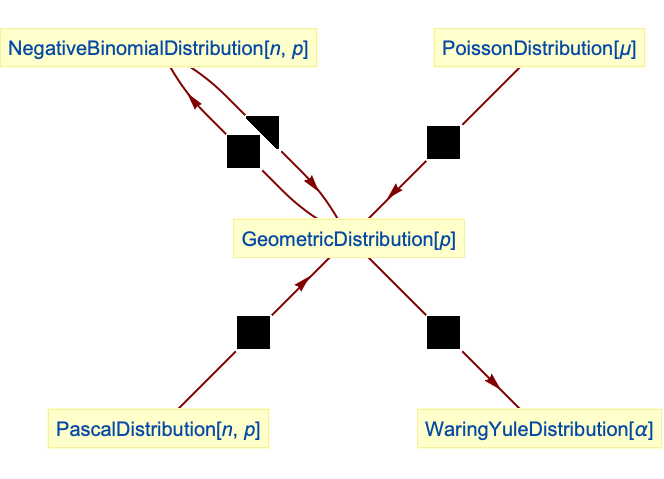
NegativeBinomialDistributionを簡約すると幾何分布になる:
![]() 個の独立した幾何学的変数の和はNegativeBinomialDistributionを示す:
個の独立した幾何学的変数の和はNegativeBinomialDistributionを示す:
幾何分布はPascalDistributionを変換したものである:
WaringYuleDistributionは幾何分布とUniformDistributionの母数混合分布である:
幾何分布はPoissonDistributionとGammaDistributionの母数混合分布である:
これはExponentialDistributionとの母数混合分布に等しい:
考えられる問題 (2)
テキスト
Wolfram Research (2007), GeometricDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/GeometricDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "GeometricDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GeometricDistribution.html.
APA
Wolfram Language. (2007). GeometricDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeometricDistribution.html