GeometricDistribution
表示概率参数 p 的一个几何分布.
更多信息
- 在一个几何分布中,对于一个非负整数,
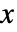 的概率是
的概率是 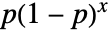 ,否则为 0. »
,否则为 0. » - GeometricDistribution[p] 表示在一系列试验中,在一次成功出现之前失败次数的分布,其中成功的概率为 p.
- GeometricDistribution 允许 p 为无量纲量. »
- GeometricDistribution 可以和诸如 Mean、CDF 和 RandomVariate 等函数一起使用. »
背景
- GeometricDistribution[p] 表示定义在整数
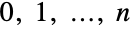 上的离散统计分布,由非负实数
上的离散统计分布,由非负实数 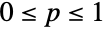 参数化. 几何分布具有单调递减的离散概率密度函数(PDF),参数 p 决定概率密度函数的高度和尖锐度. 几何分布有时候也称为Furry 分布.
参数化. 几何分布具有单调递减的离散概率密度函数(PDF),参数 p 决定概率密度函数的高度和尖锐度. 几何分布有时候也称为Furry 分布. - 几何分布有时候称为指数分布(ExponentialDistribution)的离散模拟. 它可以定义为对获得单次成功的伯努利实验数目(即服从 BernoulliDistribution 的变量的实验次数)建模. 几何分布用于对大量各种领域的不同现象建模,包括植物种群的竞争行为、票控的力度、先天畸形的详情并估算动物丰富程度. 更进一步说,几何分布广泛应用于可靠性理论,并且对气象学、排队理论和应用随机学的马可夫模型的重要部分.
- RandomVariate 可用于给出一个或多个机器精度或任意精度(后者通过 WorkingPrecision 选项)的几何分布的伪随机变元. Distributed[x,GeometricDistribution[p]],更简洁的表示为 xGeometricDistribution[p],可用于论断随机变量 x 服从几何分布. 然后这类论断可用于诸如 Probability、NProbability、Expectation 和 NExpectation 等函数中.
- 概率密度和累积分布函数可以通过使用 PDF[GeometricDistribution[p],x] 和 CDF[GeometricDistribution[p],x] 给出. 均值、中位数、方差、原始矩和中心矩可以分别使用 Mean、Median、Variance、Moment 和 CentralMoment 计算. 可以用 DiscretePlot 将这些量可视化.
- DistributionFitTest 可用于检验给定的数据集是否与几何分布相一致,EstimatedDistribution 可用于通过给定数据估计几何参数分布,而 FindDistributionParameters 可用于将数据拟合为几何分布. ProbabilityPlot 可用于生成已知数据相对于符号式几何分布的 CDF 图形,而 QuantilePlot 可用于生成已知数据相对于符号式几何分布的分位数的分位数图形.
- TransformedDistribution 可用于表示几何分布的变换,CensoredDistribution 可用于表示在上限和下限值之间删失值的分布,TruncatedDistribution 可用于表示在上限和下限值之间截断值的分布. CopulaDistribution 可用于构建包含几何分布的更高维分布,而 ProductDistribution 可用于计算独立分量分布涉及几何分布的联合分布.
- GeometricDistribution 与若干其他分布密切相关. 例如,GeometricDistribution 是广义 NegativeBinomialDistribution 的特例,因为 NegativeBinomialDistribution[1,p] 的 PDF 与 GeometricDistribution[p] 恰好相同,而且在 XiGeometricDistribution[p](对于所有
 )的情况下,
)的情况下,  的和服从 NegativeBinomialDistribution[n,p] 分布. GeometricDistribution 也是 PascalDistribution 的一个变换,并且可以视为 PoissonDistribution 和 GammaDistribution 或者 ExponentialDistribution 的参数混合,因为 ParameterMixtureDistribution[PoissonDistribution[μ],μGammaDistribution[1,(1-p)/p]] 和 ParameterMixtureDistribution[PoissonDistribution[μ],μ ExponentialDistribution[p/(1-p)]] 与 GeometricDistribution[p] 相同. GeometricDistribution 也与 WaringYuleDistribution、BinomialDistribution、PascalDistribution 和 HypergeometricDistribution 相关.
的和服从 NegativeBinomialDistribution[n,p] 分布. GeometricDistribution 也是 PascalDistribution 的一个变换,并且可以视为 PoissonDistribution 和 GammaDistribution 或者 ExponentialDistribution 的参数混合,因为 ParameterMixtureDistribution[PoissonDistribution[μ],μGammaDistribution[1,(1-p)/p]] 和 ParameterMixtureDistribution[PoissonDistribution[μ],μ ExponentialDistribution[p/(1-p)]] 与 GeometricDistribution[p] 相同. GeometricDistribution 也与 WaringYuleDistribution、BinomialDistribution、PascalDistribution 和 HypergeometricDistribution 相关.
范例
打开所有单元关闭所有单元范围 (8)
用无量纲的 Quantity 来定义 GeometricDistribution:
应用 (11)
GeometricDistribution 的 CDF 是右连续函数的一个例子:
用一个正反面出现概率相同的硬币来试验出现一个反面之前所出现正面的次数. 以下是模拟过程:
一个人站在路旁数过往的车辆,如果看到一辆红色车便重新计数. 假设20%的汽车是红色的,对计数过程进行模拟:
一个学生重复参加一个考试,直到通过为止,每次通过考试的概率为 p. 求该学生只需尝试 ![]() 次或更少次就能通过的概率:
次或更少次就能通过的概率:
已知该生通过考试所需的尝试次数小于或等于 ![]() ,求概率密度函数:
,求概率密度函数:
一个价格低廉的打火机每次打着火的概率为 90%. 模拟打火过程;结果表示成功打着火之前的失败次数:
一个麦片盒中包含 ![]() 个不同塑料动物中的一个. 这些动物出现的概率相同,并且不受其它盒子中是什么动物的影响. 模拟动物的收集过程,假设 25 个盒子有 10 种动物:
个不同塑料动物中的一个. 这些动物出现的概率相同,并且不受其它盒子中是什么动物的影响. 模拟动物的收集过程,假设 25 个盒子有 10 种动物:
在收集了 ![]() 个不同动物后,要在剩下的
个不同动物后,要在剩下的 ![]() 个动物中找到一个新的不同动物所需的盒子数服从参数为
个动物中找到一个新的不同动物所需的盒子数服从参数为 ![]() 的几何分布. 求得到新的不同动物所需盒子数的期望值:
的几何分布. 求得到新的不同动物所需盒子数的期望值:
对一个计算机内存来说,所需的数据存储在缓存中的概率是 p. 如果所需数据不在缓存中,则出现一次“高速缓存未中”. 求在第 ![]()
![]() 次内存访问时,出现“高速缓存未中”的概率:
次内存访问时,出现“高速缓存未中”的概率:
模拟在一个“高速缓存未中”出现前的“高速缓存命中”的数目,假设20%的数据放在缓存中:
假设对于缓存访问时间是 10 毫微秒而对于RAM访问时间是 1000 毫微秒. 求平均访问时间:
一个包含 ![]() 个数据包的数据流在没有任何排序信息的情况下重复发送. 求在数据流的数据包第一次以正确顺序到达之前的尝试次数的分布:
个数据包的数据流在没有任何排序信息的情况下重复发送. 求在数据流的数据包第一次以正确顺序到达之前的尝试次数的分布:
一个赌徒在一个赌场押注金额 ![]() ,比赛中没有赌金限制,获胜概率为
,比赛中没有赌金限制,获胜概率为 ![]() . 如果他输了,他就对赌金进行加倍处理,如果他获胜,则他就退出. 因此,所参加的游戏的数目服从一个几何分布, 其中参加的游戏的期望数目如下表示:
. 如果他输了,他就对赌金进行加倍处理,如果他获胜,则他就退出. 因此,所参加的游戏的数目服从一个几何分布, 其中参加的游戏的期望数目如下表示:
要实现上述策略所需的现金储备仅对于获胜几率比较大的游戏而言是有限的,其中 ![]() :
:
一个光通信系统,传输的光在接收端产生电流. 电子数目服从泊松分布和其它取决于光类型的分布的参数混合. 如果光源使用强度为 ![]() 的相干激光,那么电子数目分布是泊松分布:
的相干激光,那么电子数目分布是泊松分布:
如果光源使用热照明,那么泊松参数服从 ExponentialDistribution,其中参数为 ![]() ,则电子数目分布是:
,则电子数目分布是:
属性和关系 (8)
在 Min 下,新生成的分布族仍然是 GeometricDistribution:
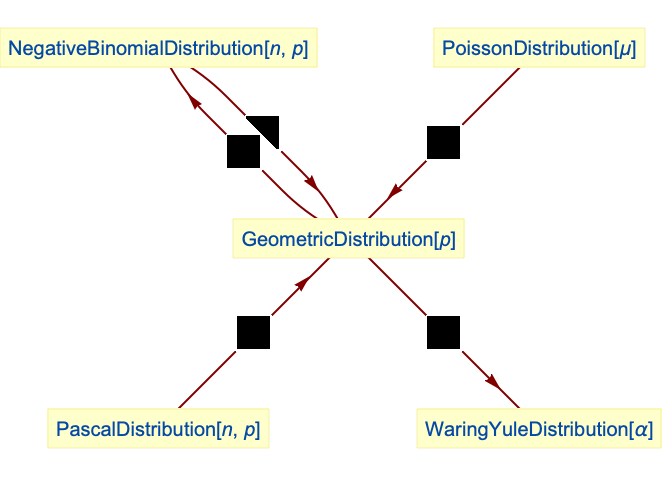
NegativeBinomialDistribution 简化为几何分布:
![]() 个独立几何分布变量的和服从 NegativeBinomialDistribution:
个独立几何分布变量的和服从 NegativeBinomialDistribution:
几何分布是 PascalDistribution 的一个变换:
WaringYuleDistribution 是几何分布和 UniformDistribution 的参数混合:
几何分布是 PoissonDistribution 和 GammaDistribution 的参数混合:
它与 ExponentialDistribution 的混合分布相同:
可能存在的问题 (2)
文本
Wolfram Research (2007),GeometricDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GeometricDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2007. "GeometricDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/GeometricDistribution.html.
APA
Wolfram 语言. (2007). GeometricDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GeometricDistribution.html 年