HypergeometricDistribution
HypergeometricDistribution[n,nsucc,ntot]
超幾何分布を表す.
詳細
- 超幾何分布は,nsucc回の成功を含むサイズ ntotの母集団からサンプルを n 個取り出したときの成功回数の分布を返す.
- HypergeometricDistributionでは,n,nsucc,および ntotは,0<n≤ntotで0≤nsucc≤ntotである任意の整数でよい.
- HypergeometricDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- HypergeometricDistribution[n,nsucc,ntot]は,
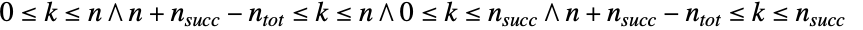 に含まれる整数値
に含まれる整数値 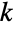 によって定義され,0<n≤ntotおよび0≤nsucc≤ntotを満足し,実験の抽選回数,母集団内の成功回数,抽選が行われる母集団のサイズをそれぞれ表す整数母数 n,nsucc,ntotによって決定される離散統計分布を表す.超幾何分布は,離散的で単峰性の確率密度関数(PDF)を持つ.この分布は,関連する数量的に類似したWalleniusの分布WalleniusHypergeometricDistribution)およびFisherの分布(FisherHypergeometricDistribution)と区別するために,中心超幾何分布,あるいは古典的超幾何分布と呼ばれることがある.
によって定義され,0<n≤ntotおよび0≤nsucc≤ntotを満足し,実験の抽選回数,母集団内の成功回数,抽選が行われる母集団のサイズをそれぞれ表す整数母数 n,nsucc,ntotによって決定される離散統計分布を表す.超幾何分布は,離散的で単峰性の確率密度関数(PDF)を持つ.この分布は,関連する数量的に類似したWalleniusの分布WalleniusHypergeometricDistribution)およびFisherの分布(FisherHypergeometricDistribution)と区別するために,中心超幾何分布,あるいは古典的超幾何分布と呼ばれることがある. - 超幾何分布は,nsuccの成功を含む大きさが ntotの母集団から(補充せずに) n 回の抽選を行った際の成功回数の分布を与え,nsucc個の青いボールと ntot-nsucc個の緑のボールが入った壷から(補充せずに) n 個のボールを取り出すモデルとして可視化することができる.超幾何分布は1710年のド・モアブル(de Moivre)の業績まで遡ることができる.ド・モアブルは,この分布を,より以前にホイヘンス(Huygens)によって提出された,上記の壷問題に関連した壷問題の解として得た.超幾何分布という名前は,この分布のPDFが一般化された超幾何関数(Hypergeometric2F1) によって表すことができることからきている.超幾何分布そのものは,さまざまな分野の数多くの数量をモデル化するために使われている.特に,待ち行列モデル,生産システム,個体群動態,分割表解析,量子暗号法の研究のツールとして使われてきた.
- RandomVariateを使って,超幾何分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,HypergeometricDistribution[n,nsucc,ntot]](より簡略な表記では xHypergeometricDistribution[n,nsucc,ntot])を使って,確率変数 x が超幾何分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[HypergeometricDistribution[n,nsucc,ntot],x]およびCDF[HypergeometricDistribution[n,nsucc,ntot],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合が超幾何分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック超幾何分布を推定することが,FindDistributionParametersを使ってデータを超幾何分布にフィットすることができる.ProbabilityPlotを使って記号超幾何分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号超幾何分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された超幾何分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って超幾何分布を含む高次元分布を構築することが,ProductDistributionを使って超幾何分布を含む独立成分分布の結合分布を計算することができる.
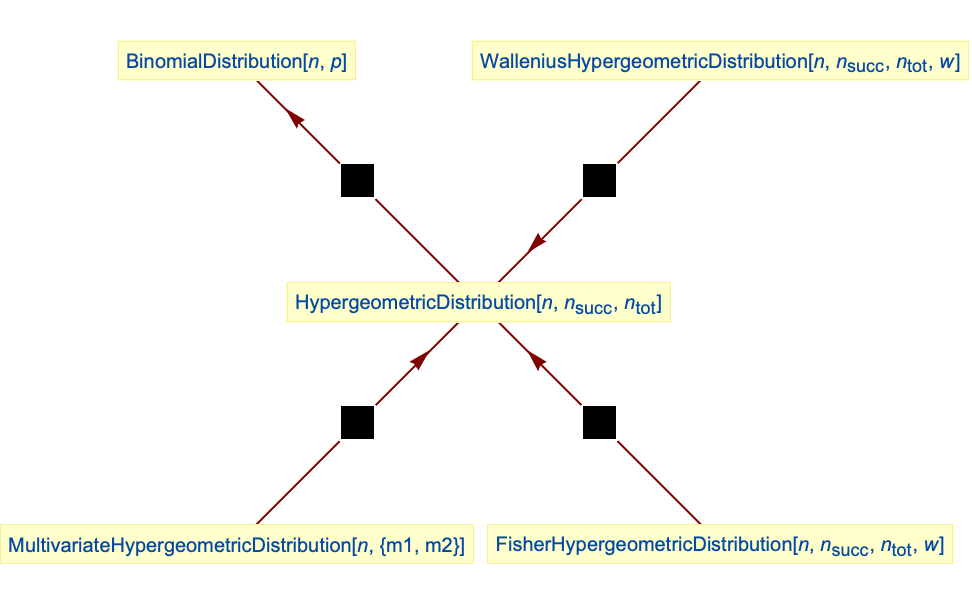
- HypergeometricDistributionは,他数多くの他の統計分布と関連している.例えば,HypergeometricDistributionは,HypergeometricDistribution[n,nsucc,ntot] がFisherHypergeometricDistribution[n,nsucc,ntot,1]とWalleniusHypergeometricDistribution[n,nsucc,ntot,1]の両方と同じPDFを持つという意味で,FisherHypergeometricDistributionとWalleniusHypergeometricDistributionの両方によって一般化される.
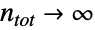 のとき,HypergeometricDistributionはBinomialDistributionの極限であり,MultivariateHypergeometricDistributionは明らかにHypergeometricDistributionの高次元一般化である.HypergeometricDistributionは,GeometricDistribution,NormalDistribution,PoissonDistribution,PearsonDistribution,BetaBinomialDistributionとも関連している.
のとき,HypergeometricDistributionはBinomialDistributionの極限であり,MultivariateHypergeometricDistributionは明らかにHypergeometricDistributionの高次元一般化である.HypergeometricDistributionは,GeometricDistribution,NormalDistribution,PoissonDistribution,PearsonDistribution,BetaBinomialDistributionとも関連している.
例題
すべて開くすべて閉じるアプリケーション (6)
HypergeometricDistributionのCDFは右連続関数の例である:
100個の要素が入った壷がある.そのうち40個が特別であるとする:
50個の要素を抽出した場合にそのうちの特別要素が20個になる確率分布を計算する:
50個の要素を抽出した場合にそのうちの特別要素が25個よりも多くなる確率を計算する:
50個の要素を抽出した場合に予想される特別要素の数を計算する:
10個一組のうち5個に欠陥がある製品があり,検査のために6個抽出したとする.見付かる欠陥品の数を数える過程のシミュレーションを行う:
ある宝くじでは一枚1ドルの券が10枚発売される.当りくじは毎回1枚のみである.元手5ドルで5つの別々の宝くじの券を1枚ずつ買った場合に当たる確率を求める:
![]() 個の白いボールと1個の青いボールが入った壷がある.2人の人が青いボールが出るまで壷からボールを取り出す.取り出したボールの替えを入れることはしない.青いボールを取り出した人が勝者となる.最初にボールを取り出した人が勝者となる確率を求める.最初に取り出した人が
個の白いボールと1個の青いボールが入った壷がある.2人の人が青いボールが出るまで壷からボールを取り出す.取り出したボールの替えを入れることはしない.青いボールを取り出した人が勝者となる.最初にボールを取り出した人が勝者となる確率を求める.最初に取り出した人が ![]() 回ボールを取り出した時点で勝つと仮定すると,それ以前の
回ボールを取り出した時点で勝つと仮定すると,それ以前の![]() 回で取り出されるボールがすべて白である確率はHypergeometricDistributionに従う:
回で取り出されるボールがすべて白である確率はHypergeometricDistributionに従う:
特性と関係 (8)
超幾何分布の特性関数はHypergeometric2F1について定義できる:
HypergeometricDistributionの母集団の上限を無限大にするとBinomialDistributionになる:
超幾何分布はFisherHypergeometricDistributionの特殊ケースである:
超幾何分布はWalleniusHypergeometricDistributionの特殊ケースである:
超幾何分布は二変量のMultivariateHypergeometricDistributionに等しい:
HypergeometricDistributionは,2つの独立二項変数の総数に条件付けして求めることができる:
考えられる問題 (4)
HypergeometricDistributionは,ntot,nsucc,n のいずれかが正ではない場合は定義されない:
HypergeometricDistributionは,n>ntotのときは定義されない:
HypergeometricDistributionは nsucc>ntot のときは定義されない:
テキスト
Wolfram Research (2007), HypergeometricDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/HypergeometricDistribution.html.
CMS
Wolfram Language. 2007. "HypergeometricDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HypergeometricDistribution.html.
APA
Wolfram Language. (2007). HypergeometricDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HypergeometricDistribution.html