WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

InverseFourierTransform

InverseFourierTransform[expr,ω,t]

expr の記号逆フーリエ変換を与える．

InverseFourierTransform[expr,{ω₁,ω₂,…},{t₁,t₂,…}]

expr の多次元逆フーリエ変換を与える．

詳細とオプション

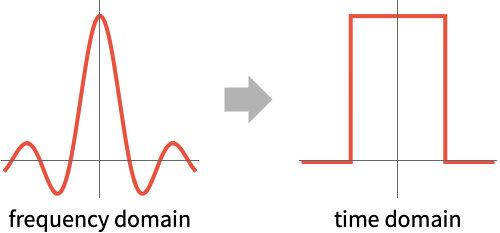
フーリエ(Fourier)変換とその逆変換は，時間領域と周波数領域間の変換を行う方法である．
フーリエ変換は，一般に，常微分方程式および偏微分方程式を簡約してそれぞれ代数方程式および常微分方程式にするために使われる．フーリエ変換は，制御理論および信号処理においても幅広く使われている．また，量子力学，ノイズ除去等の研究分野にも使われている．
周波数領域関数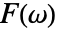の逆フーリエ変換は時間領域関数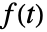である．

関数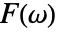の逆フーリエ変換は，デフォルトでは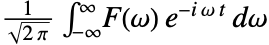で定義される．
関数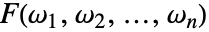の多次元逆フーリエ変換は，デフォルトで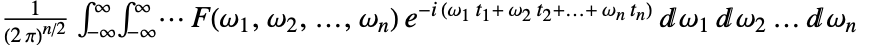，，ベクトル表記を使う場合は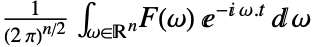と定義される．
異なった定義の選択は，オプションFourierParametersで指定できる．
積分は，第3引数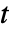が数値で与えられている場合は数値メソッドで計算される．
漸近逆フーリエ変換はAsymptoticを使って計算できる．
以下は，いくつかの関連するフーリエ変換である，

	FourierTransform	無限連続時間関数(FT)
	FourierSequenceTransform	無限離散時間関数(DTFT)
	FourierCoefficient	有限連続時間関数(FS)
	Fourier	有限離散時間関数(DFT)

逆フーリエ変換は，導関数が急速に減少する関数のSchwartzベクトル空間では自己同形であり，その双対において自己同形，緩増大分布空間，に誘導される．これには，絶対可積分関数，多項式の増加の性質の好ましい関数，コンパクトにサポートされた分布が含まれる．緩増加空間．これには，絶対可積分関数，多項式の増加の行儀のよい関数，コンパクトにサポートされた分布が含まれる．
したがって，InverseFourierTransformは絶対可積分関数に使えるだけでなく，事実上変換できる一般化された関数のプールを拡大するために，DiracDeltaのようなさまざまな緩増加分布にも使うことができる．
次のオプションを与えることができる．

	AccuracyGoal	Automatic	絶対確度の目標桁数
	Assumptions	$Assumptions	パラメータについての仮定
	FourierParameters	{0,1}	逆フーリエ余弦変換を定義するパラメータ
	GenerateConditions	False	パラメータについての条件を含む答を生成するかどうか
	PerformanceGoal	$PerformanceGoal	最適化するパフォーマンスの局面
	PrecisionGoal	Automatic	目標精度の桁数
	WorkingPrecision	Automatic	内部計算精度

以下は，FourierParametersのよく使われる設定である，

	{0,1}	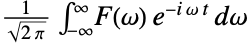	デフォルト設定／物理学
	{1,-1}	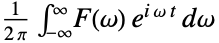	システム工学／数学
	{-1,1}		古典的物理学
	{0,-2Pi}	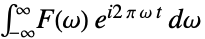	通常の周波数
	{a,b}	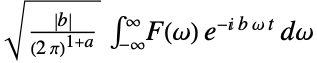	一般的な設定

TraditionalFormではInverseFourierTransformは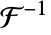，を使用して出力する． »

例題

すべて開くすべて閉じる

例 (5)

関数の逆フーリエ変換を計算する：

関数とそのフーリエ変換をプロットする：

システムエンジニアリングの慣習では，フーリエパラメータを変更する：

パラメータがある関数の逆フーリエ変換：

とについての結果をプロットする：

逆フーリエ変換の数値計算：

二変量関数の逆フーリエ変換：

変換の規模をプロットする：

スコープ (41)

基本的な用法 (3)

関数の逆フーリエ変換を記号パラメータについて計算する：

パラメータに数値を使う：

TraditionalFormによる表示：

初等関数 (7)

ベキ関数：

2つのガウス関数の逆フーリエ変換：

両方のガウス関数をプロットする：

正弦二乗関数：

平方根を含む関数：

変換の実部と虚部をプロットする：

複素指数と平方根関数を含む関数：

変換をプロットする：

逆正接関数：

大きさと位相をプロットする：

Sech関数の逆変換：

逆変換をプロットする：

有理関数 (4)

逆関数：

複素有理関数の逆フーリエ変換：

についての結果をプロットする：

二次多項式の逆：

結果をプロットする：

2つの多項式の商：

実部と虚部のプロット：

特殊関数 (6)

Sinc関数：

結果をプロットする：

BesselK関数になる逆フーリエ変換：

結果をプロットする：

BesselJ関数を含む式：

結果をプロットする：

BesselY関数の逆フーリエ変換：

結果をプロットする：

BesselJ関数になる上の平方根関数の逆変換：

結果をプロットする：

Gamma，余弦，絶対値の各関数の積：

についての結果をプロットする：

区分関数 (4)

以下の関数の逆関数は区分関数である：

逆変換をプロットする：

区分指数関数になる複素有理関数の逆変換：

逆変換をプロットする：

ボックス関数の逆変換：

区分関数の逆フーリエ変換：

周期関数 (4)

正弦と余弦の和の逆変換：

SawtoothWave：

逆変換が三角関数になる関数：

一般化された関数 (2)

指数虚関数の逆変換はDiracDelta関数である：

指数虚関数との累乗の積の逆変換はDiracDelta関数の導関数である：

多変量関数 (5)

二変量有理関数の逆フーリエ変換：

二変量指数関数の逆フーリエ変換：

逆変換がそれ自身である逆平方根関数：

逆変換をプロットする：

三変量関数の逆フーリエ変換：

三変量有理関数：

形式的な特性 (3)

一次導関数の逆フーリエ変換：

二次導関数の逆フーリエ変換：

逆フーリエ変換は方程式に縫い込まれる：

数値反転 (3)

逆フーリエ変換を単一の点で計算する：

逆フーリエ変換を記号的に計算することもできる：

次に t の特定の値で評価する：

数値逆フーリエ変換をプロットし，厳密な結果と比較する：

オプション (7)

AccuracyGoal (1)

オプションAccuracyGoalは，確度の桁数を設定する：

デフォルト設定では以下のようになる：

Assumptions (1)

BesselJの逆フーリエ変換は区分関数である：

FourierParameters (2)

単位ボックス関数および異なるパラメータについての逆フーリエ変換：

セッションごとに1回通常の周波数を扱うように，パラメータの特定の大域選択を設定する：

デフォルトに戻す：

GenerateConditions (1)

GenerateConditionsTrueを使って結果が有効になる場合のパラメータ的な条件を得る：

PrecisionGoal (1)

オプションPrecisionGoalは，積分における相対的な許容範囲を設定する：

デフォルト設定では以下のようになる：

WorkingPrecision (1)

WorkingPrecisionが指定されていると，計算はその作業精度で行われる：

デフォルト設定では以下のようになる：

アプリケーション (7)

信号とシステム (2)

信号のたたみ込みを求める：

それらのフーリエ変換の積：

逆変換を求める：

Convolveと比較する：

理想的なローパスフィルタが定義された：

インパルス応答はの逆フーリエ変換である：

そのステップ応答は以下のようになる：

常微分方程式 (1)

フーリエ変換を使って微分方程式を解く：

フーリエ変換を方程式に適用する：

フーリエ変換を解く：

逆変換を求めて解を得る：

DSolveValueと比較する：

偏微分方程式 (1)

熱伝導方程式について考える．，初期条件：

についてのフーリエ変換：

かつとして常微分方程式を解く：

逆フーリエ変換を計算する：

たたみ込みを計算して解を得る：

初期条件がでの特殊ケースについて考える：

DSolveValueと比較する：

のさまざまな値について初期条件と解をプロットする：

- 平面上で解をプロットする：

積分評価 (1)

次の定積分を計算する：

についてのフーリエ変換を計算し，変換と積分の順序を逆にする：

について積分する：

逆フーリエ変換を使って結果を得る：

Integrateと比較する：

その他のアプリケーション (2)

平面上の放射対称関数の逆フーリエ変換は，逆Hankel変換として表すことができる．以下で定義される関数についてこの関係を証明する：

関数をプロットする：

その逆フーリエ変換を計算する：

InverseHankelTransformを使って同じ結果を得る：

逆フーリエ変換をプロットする：

放射対称関数のリストについて，逆フーリエ変換の表を生成する：

これらの関数の逆Hankel変換を計算する：

必要な逆フーリエ変換の表を生成する：

特性と関係 (5)

デフォルトで，の逆フーリエ変換は以下になる：

のとき，定積分は以下のようになる：

InverseFourierTransformと比較する：

Asymptoticを使って漸近近似を計算する：

InverseFourierTransformとFourierTransformは互いに逆関数である：

InverseFourierTransformとInverseFourierCosTransformは偶関数について等しい：

InverseFourierTransformとInverseFourierSinTransformは奇関数については-分異なる：

考えられる問題 (1)

逆フーリエ変換の結果はもとと同じ形であるとは限らない：

おもしろい例題 (2)

のInverseFourierTransformは，ボックス関数ののたたみ込みである：

基本的な逆フーリエ変換の表を作成する：

トップへ