PoissonConsulDistribution[μ,λ]
母数が μ と λ のPoisson–Consul分布を表す.


PoissonConsulDistribution
PoissonConsulDistribution[μ,λ]
母数が μ と λ のPoisson–Consul分布を表す.
詳細
- PoissonConsulDistributionは一般化されたポアソン分布(GPD)としても知られる.
- Poisson–Consul分布における整数値
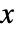 の確率は,
の確率は,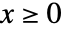 では
では 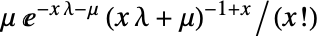 であり,
であり,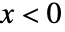 では0である.
では0である. - PoissonConsulDistributionでは,μ は任意の正の実数でよく,λ は0から1までの任意の実数でよい.
- PoissonConsulDistributionでは,μ と λ は無次元量でよい. »
- PoissonConsulDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- PoissonConsulDistribution[μ,λ]は,整数値
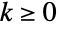 について定義され,実数母数 μ (
について定義され,実数母数 μ (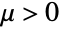 ) および λ (
) および λ (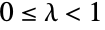 )によって決定される離散統計分布を表す.Poisson–Consul分布は,離散的で単峰性の確率密度関数(PDF)を持つ.この分布は,ポアソン分布(PoissonDistribution)が特殊ケースとして実現されることがあるという事実から,一般化されたポアソン分布と呼ばれることがある.また,ラグランジュ・ポアソン分布と呼ばれることもある.
)によって決定される離散統計分布を表す.Poisson–Consul分布は,離散的で単峰性の確率密度関数(PDF)を持つ.この分布は,ポアソン分布(PoissonDistribution)が特殊ケースとして実現されることがあるという事実から,一般化されたポアソン分布と呼ばれることがある.また,ラグランジュ・ポアソン分布と呼ばれることもある. - Poisson–Consul分布は(フランス人の数学者であるSiméon Poissonに因んで名付けられた)標準ポアソン分布を一般化したもので,1970年代から1980年代にかけて一般化された分布に関する研究を続けた統計学者のPrem C. Consulの名前を冠している.Poisson–Consul分布もまた古典的なポアソン分布と同じように出現確率が非常に低い多数の独立試行(例:1年間に馬に蹴られて死ぬ騎兵の数)からなる状況のモデル化に非常に有用で,単一の事象の出現確率が一定でなければならないという意味で古典的ポアソン分布を拡張している.Poisson–Consul分布は,家庭内暴力等の現代における多くの現象のモデル化にも使われており,金融,保険数理等の分野の貴重なツールとなっている.
- RandomVariateを使って,Poisson–Consul分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,PoissonConsulDistribution[μ,λ]](より簡略な表記では xPoissonConsulDistribution[μ,λ])を使って,確率変数 x がPoisson–Consul分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[PoissonConsulDistribution[μ,λ],x]およびCDF[PoissonConsulDistribution[μ,λ],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合がPoisson–Consul分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックPoisson–Consul分布を推定することが,FindDistributionParametersを使ってデータをPoisson–Consul分布にフィットすることができる.ProbabilityPlotを使って記号Poisson–Consul分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号Poisson–Consul分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたPoisson–Consul分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってPoisson–Consul分布を含む高次元分布を構築することが,ProductDistributionを使ってPoisson–Consul分布を含む独立成分分布の結合分布を計算することができる.
- PoissonConsulDistributionは他の多くの統計分布と関連している.この分布は,PoissonConsulDistribution[μ,0]の確率密度関数がPoissonDistribution[μ]の確率密度関数と厳密に等しいという意味で,PoissonDistributionを直接一般化したものである.加えて,PoissonConsulDistributionはBorelTannerDistributionの母数混合(ParameterMixtureDistribution)として実現でき,PoissonConsulDistribution[μ,λ]は μ→∞のときのInverseGaussianDistributionの極限である(ただし,μ (1-λ)は固定されたままであるとする).PoissonConsulDistributionは,PascalDistribution,BinomialDistribution,NegativeBinomialDistribution,MultinomialDistribution,NegativeMultinomialDistributionとも関係がある.
例題
すべて開く すべて閉じるスコープ (8)
Poisson–Consul分布から擬似乱数のサンプルを生成する:
そのヒストグラムをPoisson–Consul分布の確率密度関数と比較する:
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
μ の値が大きい場合,尖度はNormalDistributionの尖度に近くなる:
無次元のQuantityを使ってPoissonConsulDistributionを定義する:
アプリケーション (3)
PoissonConsulDistributionのCDFは右連続関数の例である:
案内係を訪れる顧客数は平均0.6でPoissonDistributionに従い,案内係が仕事を開始する時点で列に並んで待っている顧客数は平均5でPoissonDistributionに従う.待ち行列が空になるまでに対応される顧客数はPoissonConsulDistributionに従う:
繁忙期に少なくとも15人の顧客がサービス係の対応を受ける確率を求める:
母集団の初期サイズは平均 μ のPoissonDistributionに従う.各子世代のサイズもまた平均が世代のサイズに比例し定数 λ のポアソン分布に従う.子孫の総数のシミュレーションを行う:
子孫の総数はPoissonConsulDistributionに従う:
特性と関係 (5)
同じ λ 母数を持つPoissonConsulDistributionの確率変量の総和は同じ λ 母数を持つPoissonConsulDistributionに従う:
Poisson–Consul分布を簡約するとPoissonDistributionになる:
![]() が固定されているPoissonConsulDistributionの大きい μ の極限はInverseGaussianDistributionに従う:
が固定されているPoissonConsulDistributionの大きい μ の極限はInverseGaussianDistributionに従う:
PoissonConsulDistributionはBorelTannerDistributionとPoissonDistributionの母数混合である:
関連するガイド
-
▪
- 離散一変量分布
テキスト
Wolfram Research (2010), PoissonConsulDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "PoissonConsulDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html.
APA
Wolfram Language. (2010). PoissonConsulDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html
BibTeX
@misc{reference.wolfram_2025_poissonconsuldistribution, author="Wolfram Research", title="{PoissonConsulDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html}", note=[Accessed: 03-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_poissonconsuldistribution, organization={Wolfram Research}, title={PoissonConsulDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html}, note=[Accessed: 03-February-2026]}