PolyaAeppliDistribution

PolyaAeppliDistribution[θ,p]

形状母数が θ と p のPólya–Aeppli分布を表す．

詳細

  • Pólya–Aeppli分布は複合した幾何学的ポアソン分布である．つまり，独立同分布に従い，変量の数がポアソン分布に従う幾何確率変量の和の分布である．
  • Pólya–Aeppli分布における正の整数値 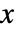の確率はp^(x-1) TemplateBox[{{1, -, x}, 2, {-, {{(, {{(, {1, -, p}, )}, , theta}, )}, /, p}}}, Hypergeometric1F1]に比例する．
  • PolyaAeppliDistributionでは，θ は任意の正の実数でよく，p は0から1までの数である．
  • PolyaAeppliDistributionでは，θ と p は無次元量でよい． »
  • PolyaAeppliDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる．

予備知識

  • PolyaAeppliDistribution[θ,p]は，整数値 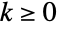について定義され，正の実数母数 θ および p（尺度母数」と呼ばれる）によって決定される離散統計分布を表す．ただし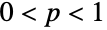，である．Pólya–Aeppli分布の確率密度関数(PDF)は，離散的で単峰性であり，全体的な形（高さ，広がり，最大値の水平位置）は θ および p の値によって決定される．Pólya–Aeppli分布は幾何学的ポアソン分布と呼ばれることがあるが，これを幾何分布(GeometricDistribution)あるいはポアソン分布(PoissonDistribution)と混同してはならない．
  • Pólya–Aeppli分布は，1920年代から1930年代にかけての，スイス人の数学者である Alfred Aeppliの博士論文とその指導教官であったGeorge Pólyaのその後の研究まで遡ることができる．Pólya–Aeppli分布分布は，独立同分布に従い，変数の数がポアソン分布(PoissonDistribution)に従う幾何学(GeometricDistribution)確率変数の和の分布であった．特に，この分布は，壺の数がポアソン分布に従い，各壺の中のビー玉の数が幾何分布に従う壺のモデルとして説明することができる．Pólya–Aeppli分布は，その始まりから計量生物学やマルコフモデルの研究で使われており，生物学，待ち行列理論，事故統計，生物情報学等の分野における現象のモデル化にも使われている．
  • RandomVariateを使って，Pólya–Aeppli分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,PolyaAeppliDistribution[θ,p]]（より簡略な表記では xPolyaAeppliDistribution[θ,p]）を使って，確率変数 x がPólya–Aeppli分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[PolyaAeppliDistribution[θ,p],x]およびCDF[PolyaAeppliDistribution[θ,p],x]を使って得られる．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．これらの数量はDiscretePlotを使って可視化することができる．
  • DistributionFitTestを使って，与えられたデータ集合がPólya–Aeppli分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックPólya–Aeppli分布を推定することが，FindDistributionParametersを使ってデータをPólya–Aeppli分布にフィットすることができる．ProbabilityPlotを使って記号Pólya–Aeppli分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号Pólya–Aeppli分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたPólya–Aeppli分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってPólya–Aeppli分布を含む高次元分布を構築することが，ProductDistributionを使ってPólya–Aeppli分布を含む独立成分分布の結合分布を計算することができる．
  • PolyaAeppliDistributionは他の多くの統計分布と関連している．この分布は，p→0のときのPolyaAeppliDistribution[θ,p]（ただし 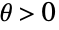）の確率密度関数の極限がPoissonDistribution[θ]の確率密度関数と厳密に等しいという意味で，PoissonDistributionを極限のケースとして持つ．PolyaAeppliDistributionは，GeometricDistribution，PoissonConsulDistribution，SkellamDistribution，CompoundPoissonDistributionとも関連がある．

例題

すべて開くすべて閉じる

例  (3)

確率質量関数：

累積分布関数：

平均と分散：

スコープ  (8)

Pólya–Aeppli分布から擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムと推定分布の確率密度関数を比較する：

歪度：

極限値：

尖度：

極限値：

母数の関数としての閉形式の種々のモーメント：

Moment：

CentralMoment：

FactorialMoment：

記号次数の閉形式：

Cumulant：

ハザード関数：

分位関数：

無次元のQuantityを使ってPolyaAeppliDistributionを定義する：

アプリケーション  (2)

PolyaAeppliDistributionのCDFは右連続関数の例である：

伝染病の温床数は平均10でPoissonDistributionに従う．一方，温床にいる患者数は平均7でGeometricDistributionに従う．患者総数が70より大きくなる確率を求める：

患者数の分布質量関数をプロットする：

特性と関係  (3)

Pólya–Aeppli分布は加法の下で閉じている：

特性関数を使った証明：

他の分布との関係：

PoissonDistributionはPólya–Aeppli分布の極限のケースである：

Wolfram Research (2010), PolyaAeppliDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), PolyaAeppliDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "PolyaAeppliDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html.

APA

Wolfram Language. (2010). PolyaAeppliDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html

BibTeX

@misc{reference.wolfram_2024_polyaaepplidistribution, author="Wolfram Research", title="{PolyaAeppliDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_polyaaepplidistribution, organization={Wolfram Research}, title={PolyaAeppliDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/PolyaAeppliDistribution.html}, note=[Accessed: 21-November-2024 ]}