WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

RegionWithin[reg1,reg2]

reg2が reg1に含まれるときにTrueを返す．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
基本的な用法  
基本的な領域  
数式定義領域  
メッシュ領域  
派生領域  
オプション  
Assumptions  
GenerateConditions  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

RegionWithin

RegionWithin[reg1,reg2]

reg2が reg1に含まれるときにTrueを返す．

詳細とオプション

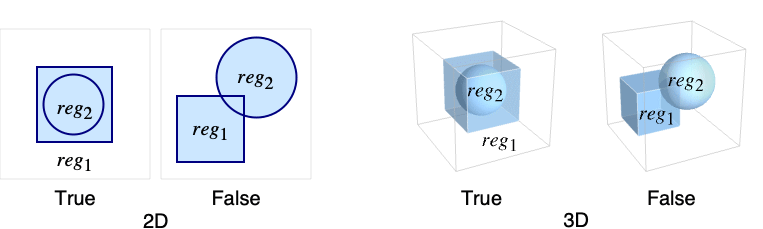
  • reg2に属するすべての点がreg1にも属するとき，領域 reg2は reg1に含まれる．
  • すべての regiがパラメータを含まない領域である，つまり，ConstantRegionQ[regi]がTrueであるとき，この領域は点集合で，一般にTrueまたはFalseが返される．
  • regiの中にパラメータに依存するものがある，つまり，ConstantRegionQ[regi]がFalseのとき，regiは領域の族を表し，RegionWithinは reg2が reg1に含まれるためのパラメータについての条件を計算しようとする．
  • 次は使用可能なオプションである．
  • Assumptions $Assumptionsパラメータについての仮定
    GenerateConditions Falseパラメータについての条件を生成するかどうか

例題

すべて開く すべて閉じる

例  (2)

ある領域が別の領域に含まれるかどうかを判定する：

Wolfram Language code: Subscript[ℛ, 1] = Disk[]; Subscript[ℛ, 2] = Rectangle[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

両者を可視化する：

Wolfram Language code: Graphics[{Opacity[0.5], {Red, Subscript[ℛ, 2]}, {Green, Subscript[ℛ, 1]}}]

ある領域が別の領域に含まれるための条件を生成する：

Wolfram Language code: Subscript[ℛ, 1] = ImplicitRegion[Subsuperscript[r, 1, 2] ≤ x^2 + y^2 ≤ Subsuperscript[r, 2, 2], {x, y}]; Subscript[ℛ, 2] = Annulus[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

スコープ  (15)

基本的な用法  (3)

帰属判定：

Wolfram Language code: Subscript[ℛ, 1] = Disk[]; Subscript[ℛ, 2] = Triangle[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: Graphics[{Opacity[0.5], {Red, Subscript[ℛ, 2]}, {Green, Subscript[ℛ, 1]}}]

ある領域が別の領域に含まれないことを示す：

Wolfram Language code: Subscript[ℛ, 1] = Parallelogram[]; Subscript[ℛ, 2] = Circle[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: Graphics[{Thick, Opacity[0.5], {Red, Subscript[ℛ, 2]}, {Green, Subscript[ℛ, 1]}}]

ある領域が別の領域の部分集合となる条件を求める：

Wolfram Language code: Subscript[ℛ, 1] = Disk[{0, 0}, r]; Subscript[ℛ, 2] = Parallelogram[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

基本的な領域  (4)

LineとIntervalを含む内の領域：

Wolfram Language code: RegionWithin[Interval[{-3, 1}], Line[{{0}, {1}}]]

Point：

Wolfram Language code: RegionWithin[Interval[{2, 2}], Point[{2}]]

Ball：

Wolfram Language code: RegionWithin[Interval[{-2, 0}], Ball[1]]

InfiniteLine：

Wolfram Language code: RegionWithin[InfiniteLine[{-3}, {1}], InfiniteLine[{0}, {1}]]

Pointを含む内の領域：

Wolfram Language code: Subscript[ℛ, 1] = Point[Tuples[Range[3], 2]]; Subscript[ℛ, 2] = Point[Tuples[Range[2], 2]];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

Line：

Wolfram Language code: Subscript[ℛ, 1] = Line[{{7, -1}, {6, -1}, {5, -1}, {3, 3}, {1, 1}, {0, 0}}]; Subscript[ℛ, 2] = Line[{{0, 0}, {3, 3}, {5, -1}}];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: Graphics[{Thick, Opacity[0.5], {Red, Subscript[ℛ, 2]}, {Green, Subscript[ℛ, 1]}}]

Polygon：

Wolfram Language code: Subscript[ℛ, 1] = Triangle[{{-1, -1}, {1, -1}, {1, 1}}]; Subscript[ℛ, 2] = Polygon[{{0, 0}, {1, 0}, {1, 1}, {0, 1}}];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: Graphics[{Opacity[0.5], {Red, Subscript[ℛ, 2]}, {Green, Subscript[ℛ, 1]}}]

DiskとEllipsoid：

Wolfram Language code: Subscript[ℛ, 1] = Ellipsoid[{0, 0}, {3, 2}]; Subscript[ℛ, 2] = Disk[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

RectangleとRegularPolygon：

Wolfram Language code: RegionWithin[RegularPolygon[r, 6], Rectangle[]]

Pointを含む内の領域：

Wolfram Language code: Subscript[ℛ, 1] = Point[Tuples[Range[5], 3]]; Subscript[ℛ, 2] = Point[Tuples[Range[3], 3]];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

Line：

Wolfram Language code: Subscript[ℛ, 1] = Line[{{7, -1, 1}, {5, -1, 0}, {0, 0, 0}}]; Subscript[ℛ, 2] = Line[{{0, 0, 0}, {3, 3, 3}, {5, -1, 0}, {7, -1, 1}}];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

Polygon：

Wolfram Language code: Subscript[ℛ, 1] = Triangle[{{2, 0, 0}, {0, 0, 2}, {0, 2, 2}}]; Subscript[ℛ, 2] = Polygon[{{1, 0, 1}, {0, 1, 2}, {1, 1, 1}, {2, 0, 0}}];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: Graphics3D[{Opacity[0.5], {Red, Subscript[ℛ, 2]}, {Green, Subscript[ℛ, 1]}}, Boxed -> False]

CuboidとHexahedron：

Wolfram Language code: Subscript[ℛ, 1] = Hexahedron[{{0, 0, 0}, {1, 0, 0}, {2, 1, 0}, {1, 1, 0}, {0, 0, 1}, {1, 0, 1}, {2, 1, 1}, {1, 1, 1}}]; Subscript[ℛ, 2] = Cuboid[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

BallとEllipsoid：

Wolfram Language code: Subscript[ℛ, 1] = Ellipsoid[{0, 0, 0}, {3, 2, 1}]; Subscript[ℛ, 2] = Ball[3];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

TetrahedronとSimplex：

Wolfram Language code: Subscript[ℛ, 1] = Simplex[{{1, 0, 1}, {1, 0, 0}, {0, 0, 1}, {1, 1, 1}}]; Subscript[ℛ, 2] = Tetrahedron[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内のCuboidとParallelepipedを含む内の領域：

Wolfram Language code: Subscript[ℛ, 1] = Parallelepiped[{-1, -1, -1, -1}, 2IdentityMatrix[4]]; Subscript[ℛ, 2] = Cuboid[{0, 0, 0, 0}, {1, 1, 1, 1}];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内のEllipsoidとBall：

Wolfram Language code: Subscript[ℛ, 1] = Ball[10]; Subscript[ℛ, 2] = Ellipsoid[Table[0, 10], Table[i, {i, 10}]];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

数式定義領域  (4)

陰的な領域：

Wolfram Language code: Subscript[ℛ, 1] = ImplicitRegion[x^2 + y^2 ≤ 1, {x, y}]; Subscript[ℛ, 2] = ImplicitRegion[1 / 2 ≤ x^2 + y^2 ≤ 1, {x, y}];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

パラメトリック領域：

Wolfram Language code: Subscript[ℛ, 1] = ParametricRegion[{r Cos[θ], r Sin[θ]}, {{r, 0, 2}, {θ, 0, 2π}}]; Subscript[ℛ, 2] = ParametricRegion[{x y, x - y}, {{x, 0, 1}, {y, 0, 1}}];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

2つの数式定義領域を比較する：

Wolfram Language code: Subscript[ℛ, 1] = ParametricRegion[{ρSqrt[4 - u^2]Cos[θ], ρSqrt[4 - u^2]Sin[θ], ρ u}, {{ρ, 0, 1}, {θ, 0, 2π}, {u, -2, 2}}]; Subscript[ℛ, 2] = ImplicitRegion[x^4 + y^4 + z^4 ≤ 1, {x, y, z}];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

一定ではない数式定義領域：

Wolfram Language code: RegionWithin[ImplicitRegion[Subsuperscript[r, 1, 2] ≤ x^2 + y^2 ≤ Subsuperscript[r, 2, 2], {x, y}], Annulus[]]

メッシュ領域  (3)

内のMeshRegionを比較する：

Wolfram Language code: Subscript[ℛ, 1] = MeshRegion[{{-1}, {2}}, Line[{1, 2}]]; Subscript[ℛ, 2] = MeshRegion[{{0}, {1}}, Line[{1, 2}]];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内の：

Wolfram Language code: Subscript[ℛ, 1] = DiscretizeGraphics[Disk[{0.5, 0}]]; Subscript[ℛ, 2] = MeshRegion[{{0, 0}, {1, 0}, {0.25, 0.5}, {0, 1}}, Polygon[{1, 2, 3, 4}]];
Wolfram Language code: Show[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内の：

Wolfram Language code: Subscript[ℛ, 1] = DiscretizeGraphics[Ball[]]; Subscript[ℛ, 2] = DiscretizeGraphics[Cuboid[]];
Wolfram Language code: Show[Subscript[ℛ, 2], Subscript[ℛ, 1]]
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内のBoundaryMeshRegionを比較する：

Wolfram Language code: Subscript[ℛ, 1] = BoundaryMeshRegion[{{-1}, {2}}, Point[{1, 2}]]; Subscript[ℛ, 2] = BoundaryMeshRegion[{{0}, {1}}, Point[{1, 2}]];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内の：

Wolfram Language code: Subscript[ℛ, 1] = BoundaryDiscretizeGraphics[Disk[{0.5, 0}]]; Subscript[ℛ, 2] = BoundaryMeshRegion[{{0, 0}, {1, 0}, {0.25, 0.5}, {0, 1}}, Line[{1, 2, 3, 4, 1}]];
Wolfram Language code: Show[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内の：

Wolfram Language code: Subscript[ℛ, 1] = BoundaryDiscretizeGraphics[Ball[]]; Subscript[ℛ, 2] = BoundaryDiscretizeGraphics[Cuboid[]];
Wolfram Language code: Show[Subscript[ℛ, 2], Subscript[ℛ, 1]]
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内のMeshRegionとBoundaryMeshRegionを比較する：

Wolfram Language code: Subscript[ℛ, 1] = ConvexHullMesh[RandomReal[{-2, 2}, {25, 2}]]; Subscript[ℛ, 2] = DelaunayMesh[RandomReal[{-1, 1}, {25, 2}]];
Wolfram Language code: Show[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

内の：

Wolfram Language code: Subscript[ℛ, 1] = ConvexHullMesh[RandomReal[{0, 1}, {25, 3}]]; Subscript[ℛ, 2] = DelaunayMesh[RandomReal[{-1, 1}, {25, 3}]];
Wolfram Language code: Show[Subscript[ℛ, 2], Subscript[ℛ, 1]]
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

派生領域  (1)

BooleanRegionを比較する：

Wolfram Language code: Subscript[ℛ, 1] = BooleanRegion[Xnor, {Disk[], Disk[{1, 0}]}]; Subscript[ℛ, 2] = Disk[{1 / 2, 0}, 1 / 4];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

オプション  (2)

Assumptions  (1)

単位円を含むすべての円板を求める：

Wolfram Language code: Subscript[ℛ, 1] = ImplicitRegion[x^2 + y^2 ≤ r^2, {x, y}]; Subscript[ℛ, 2] = Circle[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

半径が正のものだけを求める：

Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2], Assumptions -> r > 0]

GenerateConditions  (1)

単位円板が陰的に説明されたアニュラス内にある場合を求める：

Wolfram Language code: Subscript[ℛ, 1] = ImplicitRegion[Subscript[r, 1] ≤ x^2 + y^2 ≤ Subscript[r, 2], {x, y}]; Subscript[ℛ, 2] = Disk[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

結果が有効になる条件を示す：

Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2], GenerateConditions -> True]

退化した場合を明示的に許可する：

Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2], Assumptions -> Subscript[r, 1]∈Reals]

アプリケーション  (7)

点のすべての凸状の組合せはその凸包内にある：

Wolfram Language code: ℛ = ConvexHullMesh[RandomReal[1, {25, 2}]];
Wolfram Language code: convexcombos = Line[Subsets[MeshCoordinates[ℛ], {2}]];
Wolfram Language code: RegionWithin[ℛ, convexcombos]
Wolfram Language code: Show[ℛ, Epilog -> convexcombos]

指定された三角形に含まれる最大の円板を求める：

Wolfram Language code: ℛ = Triangle[{{0, 0}, {4, 0}, {3, 1}}];
Wolfram Language code: disk = Disk[{x, y}, r];
Wolfram Language code: Maximize[{r, RegionWithin[ℛ, disk]}, {x, y, r}]//Last//Simplify
Wolfram Language code: N[%]
Wolfram Language code: Graphics[{ℛ, Red, disk /. %}]

三角形に含まれる軸が平行な最大楕円を近似する：

Wolfram Language code: ellipse = Disk[{x, y}, {a, b}];
Wolfram Language code: NMaximize[{Area[ellipse], RegionWithin[ℛ, ellipse]}, {{x, 0, 4}, y, a, b}]
Wolfram Language code: Graphics[{ℛ, Red, ellipse /. Last[%]}]

指定された三角形を含む最小の円板を求める：

Wolfram Language code: ℛ = Triangle[{{0, 0}, {4, 0}, {3, 1}}];
Wolfram Language code: disk = Disk[{x, y}, r];
Wolfram Language code: Minimize[{r, RegionWithin[disk, ℛ]}, {x, y, r}]//Last
Wolfram Language code: Graphics[{disk /. %, Red, ℛ}]

三角形を含む軸が平行な最小楕円を求める：

Wolfram Language code: ellipse = Disk[{x, y}, {a, b}];
Wolfram Language code: Minimize[{Area[ellipse], RegionWithin[ellipse, ℛ]}, {x, y, a, b}]//FullSimplify
Wolfram Language code: N[%]
Wolfram Language code: Graphics[{ellipse /. Last[%], Red, ℛ}]

カリブ海の領域に完全に含まれるすべての国を求める：

Wolfram Language code: c = Entity["Ocean", "CaribbeanSea"]; sea = c["Polygon"] /. GeoPosition -> Identity;

各国の多角形：

Wolfram Language code: all = EntityValue["Country", "Polygon", "EntityAssociation"] /. GeoPosition -> Identity;

多角形がカリブ海に収まる国を選択する：

Wolfram Language code: Keys[Select[all, RegionWithin[sea, #]&]]//Sort

結果を確かめる：

Wolfram Language code: GeoEntities[c, "Country", "FullyContained" -> True]//Sort

これらの国を地図上で見る：

Wolfram Language code: GeoGraphics[{EdgeForm[Black], Polygon[c], GeoStyling[Red], Polygon[%]}]

単位長方形がアニュラス内に収まるすべての位置を可視化する：

Wolfram Language code: Subscript[ℛ, 1] = Annulus[{0, 0}, {1, 3}]; Subscript[ℛ, 2] = Rectangle[{x, y}];
Wolfram Language code: cond = RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]];
Wolfram Language code: RegionPlot[cond, {x, -3, 3}, {y, -3, 3}, Epilog -> {Red, Opacity[0.1], Subscript[ℛ, 1]}]

領域内でランダムウォークを行う：

Wolfram Language code: ℛ = Annulus[];

領域内で点をランダムな方向に動かす関数を定義する：

Wolfram Language code: walkPoint[pt_, r_, reg_] := Block[{npt = RandomPoint[Sphere[pt, r]]}, While[!RegionWithin[reg, Line[{pt, npt}]], npt = RandomPoint[Sphere[pt, r]] ]; npt ]

初期点からのランダムウォークのシミュレーションを行う：

Wolfram Language code: start = {0.5, 0.5};
Wolfram Language code: path = NestList[walkPoint[#, 0.1, ℛ]&, start, 500];

このウォークを可視化する：

Wolfram Language code: Graphics[{{Green, ℛ}, {Line[path]}, {Red, PointSize[Large], Point[start]}}]

RegionWithinを部分的な順序付けに使って同心円板を可視化する：

Wolfram Language code: regs = Disk[{0, 0}, #]& /@ RandomReal[{1 / 4, 1}, 6];
Wolfram Language code: colors = RandomColor[Hue[_], 6];

半径が大きい円板は他の円板を完全に覆う：

Wolfram Language code: Graphics[{EdgeForm[Black], Transpose[{colors, regs}]}]

帰属状態に従って領域をソートする：

Wolfram Language code: order = Ordering[regs, All, RegionWithin];

並べ替えられた円板を可視化する：

Wolfram Language code: Graphics[{EdgeForm[Black], Transpose[{colors, regs}][[order]]}]

特性と関係  (5)

RegionMemberを使った点の帰属判定：

Wolfram Language code: ℛ = Parallelogram[];
Wolfram Language code: RegionMember[ℛ, {1, 1 / 2}]

RegionWithinを使った領域の帰属判定：

Wolfram Language code: RegionWithin[ℛ, Point[{1, 1 / 2}]]
Wolfram Language code: RegionWithin[ℛ, Disk[{1, 1 / 2}, 1 / 3]]

ℛ2が ℛ1内にあるとき，ℛ2内の点はすべて ℛ1に帰属する：

Wolfram Language code: Subscript[ℛ, 1] = Rectangle[{-1, -1}, {1, 1}]; Subscript[ℛ, 2] = Disk[];
Wolfram Language code: Resolve[ForAll[{x, y}, {x, y}∈Subscript[ℛ, 2], {x, y}∈Subscript[ℛ, 1]]]
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]

2つの領域が等しいかどうかをチェックする：

Wolfram Language code: Subscript[ℛ, 1] = Parallelogram[{0, 0}, {{1, 0}, {0, 1}}]; Subscript[ℛ, 2] = Rectangle[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]] && RegionWithin[Subscript[ℛ, 2], Subscript[ℛ, 1]]
Wolfram Language code: RegionEqual[Subscript[ℛ, 1], Subscript[ℛ, 2]]

非空領域について，RegionDisjointはRegionWithinがTrueを返す場合はFalseを返す：

Wolfram Language code: Subscript[ℛ, 1] = Disk[]; Subscript[ℛ, 2] = Triangle[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: RegionDisjoint[Subscript[ℛ, 1], Subscript[ℛ, 2]]

FindInstanceを使って部分集合の条件に反する点を求める：

Wolfram Language code: Subscript[ℛ, 1] = Parallelogram[]; Subscript[ℛ, 2] = Rectangle[];
Wolfram Language code: RegionWithin[Subscript[ℛ, 1], Subscript[ℛ, 2]]
Wolfram Language code: pts = {x, y} /. FindInstance[{x, y}∈Subscript[ℛ, 1]∧{x, y}∉Subscript[ℛ, 2], {x, y}, 100];
Wolfram Language code: Graphics[{Point[pts], Opacity[0.5], {Red, Subscript[ℛ, 2]}, {Green, Subscript[ℛ, 1]}}]

RandomPointを使って部分集合の条件に反する点の一様サンプリングを求める：

Wolfram Language code: pts = RandomPoint[BooleanRegion[#1∧!#2&, {Subscript[ℛ, 1], Subscript[ℛ, 2]}], 100];
Wolfram Language code: Graphics[{Point[pts], Opacity[0.5], {Red, Subscript[ℛ, 2]}, {Green, Subscript[ℛ, 1]}}]

Reduceを使って部分集合の条件が満たされない箇所を求める：

Wolfram Language code: Reduce[{x, y}∈Subscript[ℛ, 2]∧{x, y}∉Subscript[ℛ, 1], {x, y}]
Wolfram Language code: RegionPlot[%, {x, -1, 3}, {y, -3 / 2, 5 / 2}, PlotPoints -> 60]
Wolfram Research (2017), RegionWithin, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionWithin.html.

テキスト

Wolfram Research (2017), RegionWithin, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionWithin.html.

CMS

Wolfram Language. 2017. "RegionWithin." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionWithin.html.

APA

Wolfram Language. (2017). RegionWithin. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionWithin.html

BibTeX

@misc{reference.wolfram_2026_regionwithin, author="Wolfram Research", title="{RegionWithin}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionWithin.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_regionwithin, organization={Wolfram Research}, title={RegionWithin}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionWithin.html}, note=[Accessed: 03-November-2026]}