StreamPlot3D
StreamPlot3D[{vx,vy,vz},{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
ベクトル場{vx,vy,vz}の流線を x, y, z の関数としてプロットする.
StreamPlot3D[{vx,vy,vz},{x,y,z}∈reg]
変数{x,y,z}が幾何学領域 reg にあるものとする.
詳細とオプション



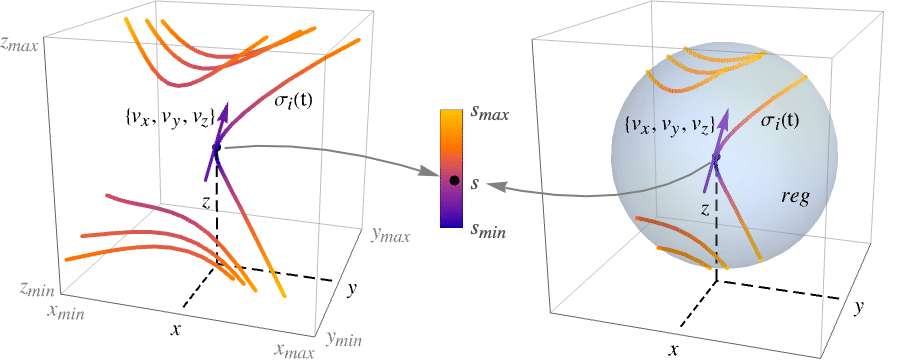
- StreamPlot3Dは,3Dストリームプロットあるいは流線プロットとして知られている.流線は,線の他に管(ストリームチューブ)やリボン(ストリームリボン)として表示することもできる.
- StreamPlot3Dは
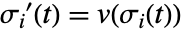 と
と 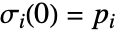 で定義される流線
で定義される流線  をプロットする.ただし,
をプロットする.ただし,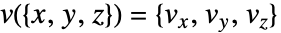 で
で 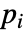 は初期流線点である.流線
は初期流線点である.流線 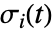 は点
は点 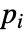 を通る曲線で,その接線は各点のベクトル場
を通る曲線で,その接線は各点のベクトル場 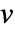 に対応する.
に対応する. - デフォルトで,流線はベクトル場
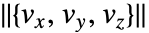 の強度
の強度 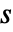 によって彩色される..
によって彩色される.. - StreamPlot3Dは,デフォルトで,プロット全体を均一な密度にするために十分な流線を表示する.背景のスカラー場は表示しない.
- StreamPlot3Dは,事実上Blockを使って,変数 x, y, z を局所的なものとして扱う.
- StreamPlot3Dは属性HoldAllを有し,x, y, z に特定の数値を割り当てた後ではじめて vi等を評価する.場合によってはEvaluateを使ってまず vi等を記号的に評価した方が効率的かもしれない.
- StreamPlot3Dには,Graphics3Dと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
BoxRatios {1,1,1} 高さと幅の割合 EvaluationMonitor None 各関数評価で評価される式 Method Automatic プロットに使用するメソッド PerformanceGoal $PerformanceGoal 最適化しようとするパフォーマンスの局面 PlotLegends None 含める凡例 PlotRange {Full,Full,Full} 含める x, y, z の値の範囲 PlotRangePadding Automatic 値の範囲をどの程度充填するか PlotTheme $PlotTheme プロットの全体的なテーマ RegionBoundaryStyle Automatic プロット領域の境界のスタイル RegionFunction True& 含める領域を決定する ScalingFunctions None 個々の座標のスケール方法 StreamColorFunction Automatic 流線の彩色方法 StreamColorFunctionScaling True StreamColorFunctionの引数をスケールするかどうか StreamMarkers Automatic 流れに使用する形状 StreamPoints Automatic 流線の数または配置 StreamScale None 流線のサイズのスケール方法 StreamStyle Automatic 流線の描画方法 WorkingPrecision MachinePrecision 内部計算精度 - RegionFunctionおよびColorFunctionの中の関数に渡される引数は x,y,z,vx,vy,vz,Norm[{vx,vy,vz}]である.
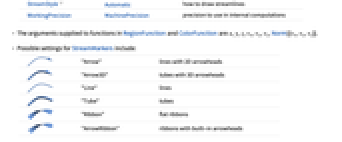
- 次は,StreamMarkersの可能な設定である.
-

"Arrow" 2Dの鏃を持つ線 
"Arrow3D" 3Dの鏃を持つ管 
"Line" 線 
"Tube" 管 
"Ribbon" 平らなリボン 
"ArrowRibbon" 組込みの鏃を持つリボン - StreamScaleAutomaticで「矢印」流線マーカーを使うと,流線の方向が分かりやすくなるように,流線が線分に分割される.
- 次は,StreamScaleの可能な設定である.
-
Automatic 流線の線分を自動的に決める Full 流線全体を分割せずに使う Tiny,Small,Medium,Large 線分の長さを指定する名前付きの設定 {len,npts,ratio} 流線の線分に明示的な指定を使う - 流線線分の長さ len は以下のいずれの形でもよい.
-
Automatic 長さを自動的に決定する None 流線を一まとまりで表示する Tiny,Small,Medium,Large 名前付きの線分長を使う s グラフィックスサイズとの割合の長さ s を使う - 各線分を描画するための点の数 npts は,Automaticまたは特定の点の数でよい.
- 縦横比 ratio は流線線分と相対的な流線の横断面の幅を指定する.
- 次は,ScalingFunctionsの可能な設定である.
-
{sx,sy,sz} scale x,y,z の各軸をスケールする - 次は,よく使われる組込みのスケーリング関数 s である.
-
"Log" 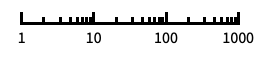
自動的に目盛ラベルを付ける対数スケール "Log10" 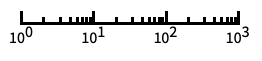
10のベキ乗に目盛を置く,10を底とした対数スケール "SignedLog" 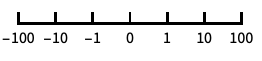
0と負の数を含む対数に似たスケール "Reverse" 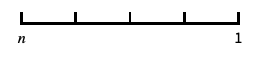
座標の向きを逆にする "Infinite" 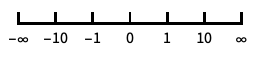
無限スケール
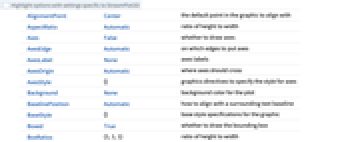
全オプションのリスト



例題
すべて開くすべて閉じるスコープ (12)
プレゼンテーション (9)
流線マーカーの「矢印」バージョンを使って流線に沿った流れの方向を示す:
流線の頭を先細りにして尾に切れ目を入れることでリボンを矢印にする:
StreamScaleを使って流線をより短い複数の線分に分割する:
オプション (42)
RegionBoundaryStyle (4)
RegionFunction (4)
場の強度が与えられた閾値を超えたところにだけ流れをプロットする:
RegionBoundaryStyleNoneを使って境界が表示されないようにする:
StreamColorFunction (4)
ColorDataからの任意の名前付き色勾配を使う:
StreamColorFunctionScalingFalseを使ってスケールされていない値を得る:
StreamColorFunctionScaling (2)
StreamMarkers (5)
StreamScale (9)
StreamStyle (3)
StreamColorFunctionはStreamStyleより優先される:
StreamColorFunctionNoneを使ってStreamStyleで流線の色を指定する:
アプリケーション (10)
流体の流れ (3)
![]() の形の点力のストークス流れについて考える.ただし,
の形の点力のストークス流れについて考える.ただし,![]() は定数ベクトル,
は定数ベクトル,![]() はディラック(Dirac)のデルタ関数である.例えば,以下は下向きの点力である:
はディラック(Dirac)のデルタ関数である.例えば,以下は下向きの点力である:
![]() かつ
かつ![]() になるようにストークス流れの方程式が満足されることを確認する:
になるようにストークス流れの方程式が満足されることを確認する:
単位球の周りのストークス流れを可視化する.流体の速度ベクトル ![]() ,圧力
,圧力 ![]() ,粘度
,粘度 ![]() ,遠方場の流体速度
,遠方場の流体速度 ![]() を定義する:
を定義する:
![]() かつ
かつ![]() となるようにストークス流れの方程式が満足されることを確認する:
となるようにストークス流れの方程式が満足されることを確認する:
電気系 (1)
![]() における点電荷近くのベクトル場のノルムが非常に速く変化するため,流線は単色のように見える.ベクトル場のノルムの大きさを領域関数で制限すると,色が表示されるようになる:
における点電荷近くのベクトル場のノルムが非常に速く変化するため,流線は単色のように見える.ベクトル場のノルムの大きさを領域関数で制限すると,色が表示されるようになる:
矢印を使ってより多くの情報を提供することができるが,矢印マーカーは矢印の先端の場の強度で彩色されるので色は変化する:
カスタムのStreamColorFunctionを使って色の制御をより強くする:
特性と関係 (9)
VectorPlot3Dを使って離散的な矢印で場を可視化する:
ListStreamPlot3DまたはListVectorPlot3Dを使ってデータに基づいてプロットを生成する:
StreamPlotを使って2Dベクトル場の流線をプロットする:
VectorPlotを使って流線の代りにベクトルでプロットする:
StreamDensityPlotを使ってスカラー場の密度プロットを加える:
VectorDensityPlotを使って流線の代りに矢印でプロットする:
LineIntegralConvolutionPlotを使ってベクトル場の線積分たたみ込みをプロットする:
VectorDisplacementPlotを使って変位ベクトル場に関連付けられた領域の変形を可視化する:
ListVectorDisplacementPlotを使って同じ変形をデータに基づいて可視化する:
SliceVectorPlot3Dで曲面に沿ってベクトルをプロットする:
VectorDisplacementPlot3Dを使って変位ベクトル場に関連付けられた3D領域の変形を可視化する:
ListVectorDisplacementPlot3Dを使って同じ変形をデータに基づいて可視化する:
ComplexVectorPlotまたはComplexStreamPlotを使って複素変数の複素関数をベクトル場としてあるいは流線を使って可視化する:
GeoVectorPlotを使って地図上にベクトルをプロットする:
GeoStreamPlotを使ってベクトルの代りに流線をプロットする:
考えられる問題 (3)
管のStreamMarkersはBoxRatiosで歪む可能性がある:
BoxRatiosを注意深く調整することで管のねじれが除去できる:
"Arrow"と"Arrow3D"の流線マーカーの色は矢印の先端で決定されるため,長い矢印の場合は色に一貫性がなくなることがある:
テキスト
Wolfram Research (2021), StreamPlot3D, Wolfram言語関数, https://reference.wolfram.com/language/ref/StreamPlot3D.html (2022年に更新).
CMS
Wolfram Language. 2021. "StreamPlot3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/StreamPlot3D.html.
APA
Wolfram Language. (2021). StreamPlot3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StreamPlot3D.html