StreamPlot3D[{vx,vy,vz},{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
绘制作为 x、y 和 z 的函数的向量场 {vx,vy,vz} 的流线.
StreamPlot3D[{vx,vy,vz},{x,y,z}∈reg]
将变量 {x,y,z} 视为位于几何区域 reg 中.




StreamPlot3D
StreamPlot3D[{vx,vy,vz},{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
绘制作为 x、y 和 z 的函数的向量场 {vx,vy,vz} 的流线.
StreamPlot3D[{vx,vy,vz},{x,y,z}∈reg]
将变量 {x,y,z} 视为位于几何区域 reg 中.
更多信息和选项




- StreamPlot3D 被称为三维流图或流线图. 除了线,流线还可以显示为管(流管)和带(流带).
- StreamPlot3D 绘制由
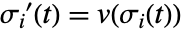 和
和 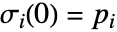 定义的流线
定义的流线  ,其中
,其中  和
和 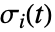 是初始流点. 流线
是初始流点. 流线  是通过点
是通过点 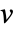 的曲线,其切线对应于各点处的矢量场
的曲线,其切线对应于各点处的矢量场 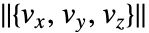 .
. - 流线默认根据矢量场
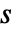 的大小
的大小  着色.
着色. - StreamPlot3D 缺省情况下显示足够多的流线,从而使得整个图形的密度大致均匀,且不显示背景标量场.
- StreamPlot3D 将变量 x、y 和 z 视为局部变量,实际上相当于使用 Block.
- StreamPlot3D 具有属性 HoldAll,仅在指定 x、y 和 z 的数值后才计算 vi 等等. 有些情况下,先用 Evaluate 符号式计算 vi 等会更有效.
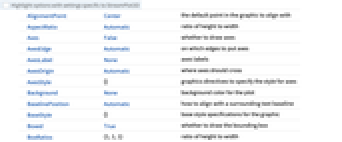
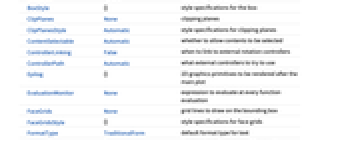
- StreamPlot3D 有和 Graphics 相同的选项,不同之处及更多选项如下所示: [所有选项的列表]
-
BoxRatios {1,1,1} 高宽比 EvaluationMonitor None 每次运行函数时要计算的表达式 Method Automatic 绘图时使用的方法 PerformanceGoal $PerformanceGoal 优化的目标 PlotLegends None 包含的图例 PlotRange {Full,Full,Full} 包含的 x、y、z 值的范围 PlotRangePadding Automatic 对数值范围进行多少填充 PlotTheme $PlotTheme 绘图的整体外观主题 RegionBoundaryStyle Automatic 怎样设置绘图区域边界的样式 RegionFunction True& 确定要包含的区域 ScalingFunctions None 怎样缩放个别坐标 StreamColorFunction Automatic 如何为流线着色 StreamColorFunctionScaling True 是否缩放传递给 StreamColorFunction 的参数 StreamMarkers Automatic 流的形状 StreamPoints Automatic 流线的数量和流线的放置 StreamScale None 如何缩放流线的大小 StreamStyle Automatic 如何绘制流线 WorkingPrecision MachinePrecision 内部计算使用的精度 - 提供给 RegionFunction 和 StreamColorFunction 中的函数的参数为 x,y,z,vx,vy,vz,Norm[{vx,vy,vz}].
- StreamMarkers 的可能的设置包括:
-

"Arrow" 带有 2D 箭头的线段 
"Arrow3D" 带有 3D 箭头的管状线段 
"Line" 线段 
"Tube" 管状线段 
"Ribbon" 扁平丝带 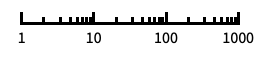
"ArrowRibbon" 带有内置箭头的丝带 - 如果设置 StreamScaleAutomatic 并使用 "arrow" 流线标记,流线将被分割为多个线段,以便于查看流线的方向.
- StreamScale 的可能的设置包括:
-
Automatic 自动确定流线的线段 Full 将流线显示为一个整体 Tiny,Small,Medium,Large 表明线段长度的已命名设置 {len,npts,ratio} 使用明确的流线线段指定 - 流线线段的长度 len 可为以下形式之一:
-
Automatic 自动确定长度 None 将流线显示为一个整体 Tiny,Small,Medium,Large 使用已命名的线段长度 s 使用与图形大小的比例为 s 的长度 - 用来画出每个线段的点数 npts 可以是 Automatic 或特定的点数.
- 比值 ratio 指定流线的截面相对于线段的宽度.
- ScalingFunctions 的可能设置包括:
-
{sx,sy,sz} 缩放 x、y 和 z 坐标 - 常见的内置缩放函数 s 包括:
-
"Log" 
对数刻度,自动进行标记 "Log10" 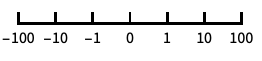
以 10 为底的对数刻度,用 10 的幂进行标记 "SignedLog" 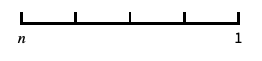
类似对数的刻度,包含 0 和负数 "Reverse" 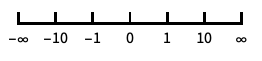
反转坐标的方向 "Infinite" 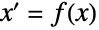
无穷刻度

所有选项的列表




范例
打开所有单元 关闭所有单元范围 (12)
演示 (9)
用 StreamScale 把流线分成多个较短的线段:
选项 (70)
ImageSize (7)
RegionBoundaryStyle (4)
RegionFunction (4)
StreamColorFunction (4)
StreamColorFunctionScaling (2)
StreamMarkers (5)
StreamScale (9)
StreamStyle (3)
StreamColorFunction 的优先级比 StreamStyle 高:
设置 StreamColorFunctionNone,通过 StreamStyle 指定流线的颜色:
Ticks (6)
应用 (10)
流体的流动 (3)
来考虑形为 ![]() 的点力的 Stokes 流,其中
的点力的 Stokes 流,其中 ![]() 是常向量,
是常向量,![]() 是 Dirac delta 函数. 例如,向下的力:
是 Dirac delta 函数. 例如,向下的力:
可视化单位球体周围的 Stokes 流. 定义流体的速度向量 ![]() 、压力
、压力 ![]() 、粘度
、粘度 ![]() 和远场流体速度
和远场流体速度 ![]() :
:
电子系统 (1)
由于向量场的范数在 ![]() 处的点电荷附近的变化异常快速,因此流线的颜色似乎都一样. 将向量场范数的幅值与区域函数绑定在一起即可显示出不同的颜色:
处的点电荷附近的变化异常快速,因此流线的颜色似乎都一样. 将向量场范数的幅值与区域函数绑定在一起即可显示出不同的颜色:
可添加箭头来提供更多信息,但是颜色会发生变化,因为箭头标记是根据箭头尖端处的场强度来着色的:
使用自定义的 StreamColorFunction 对颜色施加更多控制:
属性和关系 (9)
通过 VectorPlot3D 用离散的箭头可视化场:
用 ListStreamPlot3D 或 ListVectorPlot3D 根据数据绘图:
用 StreamPlot 绘制二维向量场的流线:
通过 VectorPlot 用向量而不是流线绘图:
使用 StreamDensityPlot 添加标量场的密度图:
通过 VectorDensityPlot 用箭头而不是流线绘图:
用 LineIntegralConvolutionPlot 绘制向量场的线积分卷积:
使用 VectorDisplacementPlot 可视化与位移矢量场相关的区域的变形:
使用 ListVectorDisplacementPlot 根据数据可视化相同的变形:
用 SliceVectorPlot3D 沿曲面绘制向量:
使用 VectorDisplacementPlot3D 可视化与位移矢量场相关的三维区域的变形:
使用 ListVectorDisplacementPlot3D 根据数据可视化相同的变形:
使用 ComplexVectorPlot 或 ComplexStreamPlot 将复变量的复函数可视化为向量场或流线:
用 GeoVectorPlot 在地图上绘制矢量:
使用 GeoStreamPlot 绘制流线而不是矢量:
可能存在的问题 (3)
管状 StreamMarkers 可能被 BoxRatios 扭曲:
仔细调整 BoxRatios 可消除失真现象:
文本
Wolfram Research (2021),StreamPlot3D,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StreamPlot3D.html (更新于 2022 年).
CMS
Wolfram 语言. 2021. "StreamPlot3D." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/StreamPlot3D.html.
APA
Wolfram 语言. (2021). StreamPlot3D. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StreamPlot3D.html 年
BibTeX
@misc{reference.wolfram_2025_streamplot3d, author="Wolfram Research", title="{StreamPlot3D}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/StreamPlot3D.html}", note=[Accessed: 20-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_streamplot3d, organization={Wolfram Research}, title={StreamPlot3D}, year={2022}, url={https://reference.wolfram.com/language/ref/StreamPlot3D.html}, note=[Accessed: 20-February-2026]}