StudentTDistribution

StudentTDistribution[ν]

自由度 ν の標準的なスチューデント(Student)の 分布を表す．

StudentTDistribution[μ,σ,ν]

位置母数 μ，尺度母数 σ，自由度 ν のスチューデントの 分布を表す．

詳細

  • 自由度 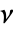のスチューデントの 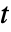分布における値 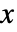の確率密度は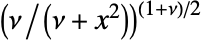に比例する． »
  • 位置母数が μ で尺度母数が σ，自由度 ν のスチューデントの 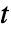分布に従う 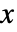については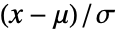， は自由度 ν の標準的なスチューデントの 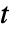分布に従う．
  • 整数 ν について，スチューデントの 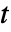分布は，正規分布からサンプルとして取った ν 個の値の観測された平均値を真の平均から引いた値の分布をサンプルの標準偏差で正規化して与える．
  • StudentTDistributionでは μ は任意の実数，σ と ν は任意の正の実数でよい．
  • StudentTDistribution では，μ と σ は単位次元が等しい任意の数量でよく，ν は任意の無次元量でよい． »
  • StudentTDistributionは，Mean，CDF，RandomVariate等の関数で使うことができる． »

予備知識

  • StudentTDistribution[μ,σ,ν]は，実数集合上で定義・サポートされ，実数 μ（「位置母数」と呼ばれる）および正の実数 σ と ν（それぞれ「尺度母数」，自由度」と呼ばれる）でパラメータ化された連続統計分布を表す．これらの母数は，ともにその確率密度関数(PDF)の全体的な動作を決定する．一般に，スチューデントの 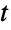分布のPDFは単一の「峰」（大域的最大値）を持つ単峰性であるが，その全体的な形（高さ，広がり，最大値の水平位置）は μ，σ，ν の値で決定される．加えて，PDFの裾部はPDFが 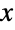の大きい値に対して指数的というよりむしろ代数的に減少するという意味で「太い」（この動作は分布のSurvivalFunctionを解析することで数量的に厳密にできる）．母数が1つの形StudentTDistribution[ν]はStudentTDistribution[0,1,ν]に等しい．母数が3つの形StudentTDistribution[μ,σ,ν]は一般化されたスチューデントの 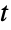分布と呼ばれることがある．
  • スチューデントの 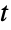分布は，1908年に英国人の統計学者William Gossetによってはじめて考案された（出版にあたっては仮の「スチューデント」が使われた）．Gossetは，正規化され正規分布に従う確率変量のサンプルが ν 個与えられた場合に，整数 ν について，スチューデントの 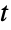分布が厳密に真の母集団平均からの観察された平均の逸脱の分布であることを示した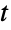． 分布は統計分野で幅広く使われており，仮定検定，分散検定の分析，ベイズ分析，確率過程でよく使われるツールである．この分布は，株価変動，電気通信における位相微分，ノイズのモデル化，画像分析等の現象のモデル化で，多くの分野で幅広く使われている．
  • RandomVariateを使って，スチューデントの 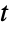分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,StudentTDistribution[μ,σ,ν]]より簡略な表記では xStudentTDistribution[μ,σ,ν]）を使って，確率変数 x がスチューデントの 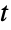分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • スチューデントの 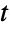分布の確率密度関数および累積分布関数は，PDF[StudentTDistribution[μ,σ,ν],x]およびCDF[StudentTDistribution[μ,σ,ν],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がスチューデントの 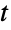分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックスチューデントの 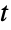分布を推定することが，FindDistributionParametersを使ってデータをスチューデントの 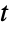分布にフィットすることができる．ProbabilityPlotを使って記号スチューデントの 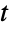分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号スチューデントの 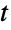分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
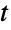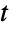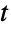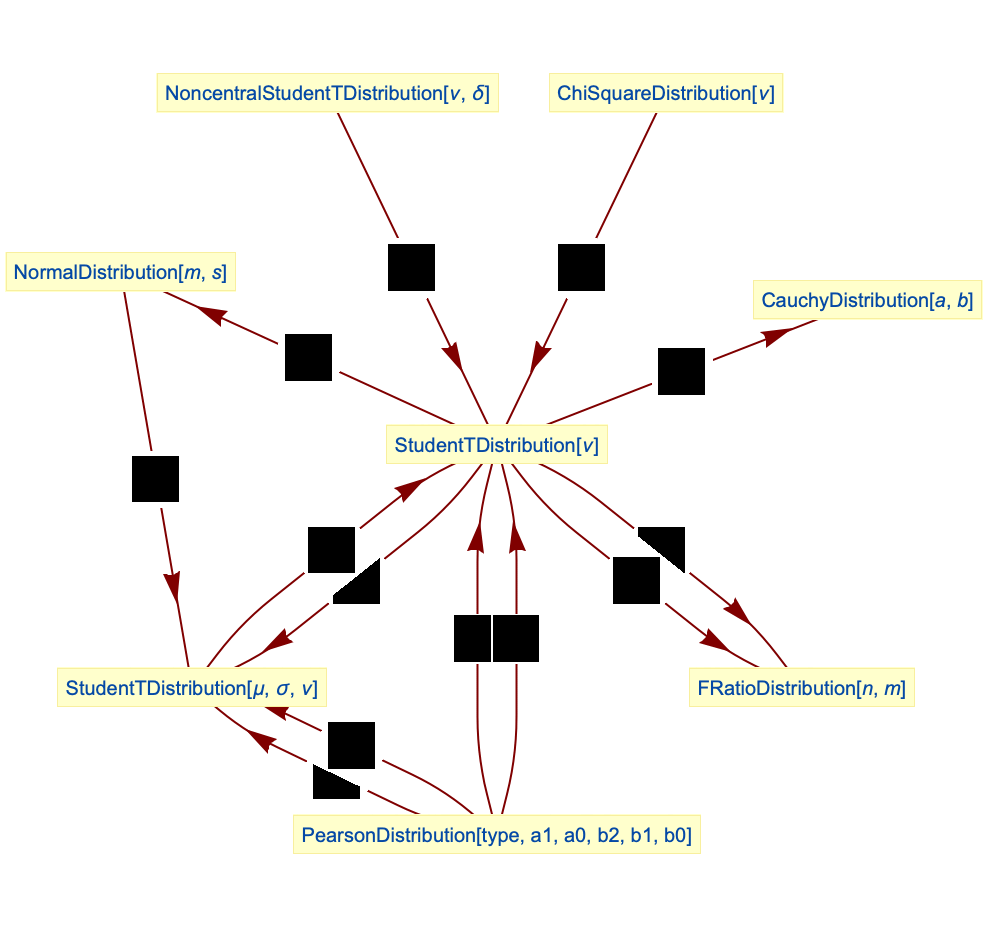
  • TransformedDistributionを使って変換されたスチューデントの 分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってスチューデントの 分布を含む高次元分布を構築することが，ProductDistributionを使ってスチューデントの 分布を含む独立成分分布の結合分布を計算することができる．
  • StudentTDistributionは，他の数多くの分布と関連がある．StudentTDistributionは，StudentTDistribution[ν]のPDFがNoncentralStudentTDistribution[ν,0]のPDFと厳密に等しいという意味でNoncentralStudentTDistributionの特殊ケースであり，また，さまざまな意味でPearsonDistributionの一般化でもある．StudentTDistribution[ν]は，ν→∞でNormalDistribution[]に近付くのに対し，StudentTDistributionのPDFはFRatioDistribution，ChiSquareDistribution，NormalDistributionの変換(TransformedDistribution)として，またNormalDistributionとGammaDistributionの母数混合 (ParameterMixtureDistribution)として得ることができる．StudentTDistributionはCauchyDistribution，MultivariateTDistribution，ChiDistributionとも密接に関係している．

例題

すべて開くすべて閉じる

例  (8)

確率密度関数：

累積分布関数：

平均と分散：

中央値：

一般化されたスチューデント 分布の確率密度関数：

一般化されたスチューデント 分布の累積分布関数：

一般化されたスチューデント 分布の平均と分散：

一般化されたスチューデント 分布の中央値：

スコープ  (8)

スチューデントの 分布から擬似乱数のサンプルを生成する：

これのヒストグラムと確率密度関数を比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

スチューデント 分布は対称的であり，したがって歪度は定義されている場合は0である：

尖度：

尺度母数と位置母数を追加しても尖度は変わらない：

極限では，尖度はNormalDistribution尖度と等しくなる：

母数の関数としての閉形式の種々のモーメント：

Moment：

記号次数の閉形式：

一般化されたスチューデント 分布のMoment：

CentralMoment：

記号次数の閉形式：

一般化されたスチューデント 分布のCentralMoment：

記号次数の閉形式：

FactorialMoment：

一般化されたスチューデント 分布のFactorialMoment：

Cumulant：

一般化されたスチューデント 分布のCumulant：

ハザード関数：

一般化されたスチューデント 分布のハザード関数：

分位関数：

一般化されたスチューデント 分布について：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

四分位数を求める：

アプリケーション  (2)

自由度 ，対立仮説 で， テストのための 値を計算する：

対立仮説 ：

対立仮説 TemplateBox[{X}, Abs]>TemplateBox[{t}, Abs]：

StudentTDistributionは厳密な（小さい）サンプリング理論で使われる． 統計を定義する：

データが正規分布からのものであれば，たとえデータが小さいサイズ（30未満）のサンプルであっても 統計はStudentTDistributionに従う：

特性と関係  (16)

スチューデント 分布は平行移動と正の因子によるスケーリングの下では閉じている：

StudentTDistribution[ν]は となるに従って正規分布に収束する：

他の分布との関係：

StudentTDistribution[ν]は位置母数 と尺度母数 を持つ：

2つの形式は変数を変えることで関連する：

StudentTDistribution[1]はCauchyDistribution[0,1]に等しい：

スチューデントの 分布は，ν が無限に近付くにつれ，標準NormalDistributionに収束する：

StudentTDistributionは非心度0のNoncentralStudentTDistributionである：

スチューデント 分布に従う変数の平方はFRatioDistributionを示す：

スチューデント 分布に従う変数の逆二乗はFRatioDistributionに従う：

スチューデント 分布はタイプ4とタイプ7のピアソン分布(PearsonDistribution)の特殊ケースである：

一般化されたスチューデント 分布はタイプ4とタイプ7のピアソン分布(PearsonDistribution)の特殊ケースである：

スチューデント 分布はChiSquareDistributionから得ることができる：

スチューデント 分布はNormalDistributionとChiSquareDistributionから得ることができる：

スチューデント 分布はNormalDistributionとGammaDistributionの母数混合分布である：

恒等スケール行列を持つMultivariateTDistributionの周辺分布はスチューデント 分布に従う：

2つのスチューデント 分布の中心モーメントは定義されている場合には互いに比例する：

考えられる問題  (2)

StudentTDistributionは，ν が正の実数ではないときは定義されない：

記号出力に無効な母数値を代入すると意味のない結果となる：

おもしろい例題  (1)

累積分布関数の等高線を持つ ν のさまざまな値についての確率密度関数：

Wolfram Research (2007), StudentTDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/StudentTDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2007), StudentTDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/StudentTDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2007. "StudentTDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/StudentTDistribution.html.

APA

Wolfram Language. (2007). StudentTDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StudentTDistribution.html

BibTeX

@misc{reference.wolfram_2024_studenttdistribution, author="Wolfram Research", title="{StudentTDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/StudentTDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_studenttdistribution, organization={Wolfram Research}, title={StudentTDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/StudentTDistribution.html}, note=[Accessed: 21-November-2024 ]}