

SymmetricMatrixQ
Details and Options

- A matrix m is symmetric if m==Transpose[m].
- SymmetricMatrixQ works for symbolic as well as numerical matrices.
- The following options can be given:
-
SameTest Automatic function to test equality of expressions Tolerance Automatic tolerance for approximate numbers - For exact and symbolic matrices, the option SameTest->f indicates that two entries mij and mkl are taken to be equal if f[mij,mkl] gives True.
- For approximate matrices, the option Tolerance->t can be used to indicate that all entries Abs[mij]≤t are taken to be zero.
- For matrix entries Abs[mij]>t, equality comparison is done except for the last
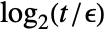 bits, where
bits, where 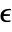 is $MachineEpsilon for MachinePrecision matrices and
is $MachineEpsilon for MachinePrecision matrices and 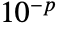 for matrices of Precision
for matrices of Precision 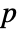 .
.
Examples
open all close allBasic Examples (2)
Scope (10)
Basic Uses (6)
Test if a real machine-precision matrix is symmetric:
A real symmetric matrix is also Hermitian:
Test if a complex matrix is symmetric:
A complex symmetric matrix has symmetric real and imaginary parts:
Test if an exact matrix is symmetric:
Use SymmetricMatrixQ with an arbitrary-precision matrix:
A random matrix is typically not symmetric:
Use SymmetricMatrixQ with a symbolic matrix:
The matrix becomes symmetric when ![]() :
:
SymmetricMatrixQ works efficiently with large numerical matrices:
Special Matrices (4)
Use SymmetricMatrixQ with sparse matrices:
Use SymmetricMatrixQ with structured matrices:
Use with a QuantityArray structured matrix:
The identity matrix is symmetric:
HilbertMatrix is symmetric:
Options (2)
SameTest (1)
This matrix is symmetric for a positive real ![]() , but SymmetricMatrixQ gives False:
, but SymmetricMatrixQ gives False:
Use the option SameTest to get the correct answer:
Tolerance (1)
Generate a real-valued symmetric matrix with some random perturbation of order 10-14:
Adjust the option Tolerance to accept this matrix as symmetric:
The norm of the difference between the matrix and its transpose:
Applications (13)
Generating Symmetric Matrices (4)
Any matrix generated from a symmetric function ![]() is symmetric:
is symmetric:
Using Table generates a symmetric matrix:
SymmetrizedArray can generate matrices (and general arrays) with symmetries:
Convert back to an ordinary matrix using Normal:
Check that matrices drawn from GaussianOrthogonalMatrixDistribution are symmetric:
Matrices drawn from CircularOrthogonalMatrixDistribution are symmetric and unitary:
Every Jordan matrix is similar to a symmetric matrix. Since any square matrix is similar to its Jordan form, this means that any square matrix is similar to a symmetric matrix. Define a function for generating an ![]() Jordan block for eigenvalue
Jordan block for eigenvalue ![]() :
:
For example, here is the Jordan matrix of dimension 4 for the eigenvalue ![]() :
:
Define a function for generating a corresponding complex similarity transformation:
The matrix is a sum of ![]() times the identity matrix and
times the identity matrix and ![]() times the backward identity matrix:
times the backward identity matrix:
Then ![]() is symmetric, which shows that the Jordan matrix is similar to a symmetric matrix:
is symmetric, which shows that the Jordan matrix is similar to a symmetric matrix:
Examples of Symmetric Matrices (5)
The Hessian matrix of a function is symmetric:
Many special matrices are symmetric, including FourierMatrix:
And HilbertMatrix:
Many filter kernel matrices are symmetric, including DiskMatrix:
AdjacencyMatrix of an undirected graph is symmetric:
As is KirchhoffMatrix:
Visualize adjacency and Kirchhoff matrices for different graphs:
Several statistical measures are symmetric matrices, including Covariance:
Uses of Symmetric Matrices (4)
A positive-definite, real symmetric matrix or metric ![]() defines an inner product by
defines an inner product by ![]() :
:
Verify that ![]() is in fact symmetric and positive definite:
is in fact symmetric and positive definite:
Orthogonalize the standard basis of ![]() to find an orthonormal basis:
to find an orthonormal basis:
Confirm that this basis is orthonormal with respect to the inner product ![]() :
:
The moment of inertia tensor is the equivalent of mass for rotational motion. For example, kinetic energy is ![]() , with
, with ![]() taking the place of the mass
taking the place of the mass ![]() and angular velocity
and angular velocity ![]() taking the place of linear velocity
taking the place of linear velocity ![]() in the formula
in the formula ![]() .
. ![]() can be represented by a positive-definite symmetric matrix. Compute the moment of inertia for a tetrahedron with endpoints at the origin and positive coordinate axes:
can be represented by a positive-definite symmetric matrix. Compute the moment of inertia for a tetrahedron with endpoints at the origin and positive coordinate axes:
Verify that the matrix is symmetric:
Compute the kinetic energy if its angular velocity is ![]() :
:
The kinetic energy is positive as long as ![]() is nonzero, showing the matrix was positive definite:
is nonzero, showing the matrix was positive definite:
Determine if a sparse matrix is structurally symmetric:
But it is structurally symmetric:
Use a different method for symmetric matrices, with failover to a general method:
Construct real-valued matrices for testing:
For a non-symmetric matrix m, the function myLS just uses Gaussian elimination:
For a symmetric indefinite matrix ms, try Cholesky and continue with Gaussian elimination:
For a symmetric positive-definite matrix mpd, try Cholesky, which succeeds:
Properties & Relations (14)
SymmetricMatrixQ[x] trivially returns False for any x that is not a matrix:
A matrix is symmetric if mTranspose[m]:
A real-valued symmetric matrix is Hermitian:
But a complex-valued symmetric matrix may not be:
Use Symmetrize to compute the symmetric part of a matrix:
This equals the average of m and Transpose[m]:
Any matrix can be represented as the sum of its symmetric and antisymmetric parts:
Use AntisymmetricMatrixQ to test whether a matrix is antisymmetric:
If ![]() is a symmetric matrix with real entries, then
is a symmetric matrix with real entries, then ![]() is antihermitian:
is antihermitian:
MatrixExp[I m] for real symmetric m is unitary:
A real-valued symmetric matrix is always a normal matrix:
A complex-valued symmetric matrix need not be normal:
Real-valued symmetric matrices have all real eigenvalues:
Use Eigenvalues to find eigenvalues:
Note that a complex-valued symmetric matrix may have both real and complex eigenvalues:
CharacteristicPolynomial[m,x] for real symmetric m can be factored into linear terms:
Real-valued symmetric matrices have a complete set of eigenvectors:
As a consequence, they must be diagonalizable:
Use Eigenvectors to find eigenvectors:
Note that a complex-valued symmetric matrix need not have these properties:
The inverse of a symmetric matrix is symmetric:
Matrix functions of symmetric matrices are symmetric, including MatrixPower:
And any univariate function representable using MatrixFunction:
SymmetricMatrix can be used to explicitly construct symmetric matrices:
These satisfy SymmetricMatrixQ:
Possible Issues (1)
SymmetricMatrixQ uses the definition ![]() for both real- and complex-valued matrices:
for both real- and complex-valued matrices:
These complex matrices need not be normal or possess many properties of self-adjoint (real symmetric) matrices:
HermitianMatrixQ tests the condition ![]() for self-adjoint matrices:
for self-adjoint matrices:
Alternatively, test if the entries are real to restrict to real symmetric matrices:
Neat Examples (1)
Images of symmetric matrices including FourierMatrix:
Related Guides
Text
Wolfram Research (2008), SymmetricMatrixQ, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html (updated 2014).
CMS
Wolfram Language. 2008. "SymmetricMatrixQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html.
APA
Wolfram Language. (2008). SymmetricMatrixQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html
BibTeX
@misc{reference.wolfram_2025_symmetricmatrixq, author="Wolfram Research", title="{SymmetricMatrixQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html}", note=[Accessed: 28-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_symmetricmatrixq, organization={Wolfram Research}, title={SymmetricMatrixQ}, year={2014}, url={https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html}, note=[Accessed: 28-January-2026]}