VectorDisplacementPlot[{vx,vy},{x,xmin,xmax},{y,ymin,ymax}]
ベクトル場{vx,vy}の変位図プロットを x と y の関数として生成する.
VectorDisplacementPlot[{vx,vy},{x,y}∈reg]
幾何学領域 reg 上に変位図をプロットする.
VectorDisplacementPlot[{{vx,vy},s},…]
スカラー場 s を使って変位図にスタイル付けする.




VectorDisplacementPlot
VectorDisplacementPlot[{vx,vy},{x,xmin,xmax},{y,ymin,ymax}]
ベクトル場{vx,vy}の変位図プロットを x と y の関数として生成する.
VectorDisplacementPlot[{vx,vy},{x,y}∈reg]
幾何学領域 reg 上に変位図をプロットする.
VectorDisplacementPlot[{{vx,vy},s},…]
スカラー場 s を使って変位図にスタイル付けする.
詳細とオプション


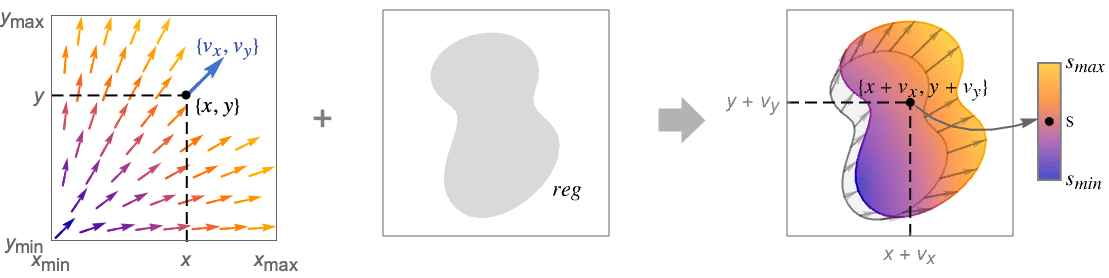
- VectorDisplacementPlotはベクトル場{vx,vy}を使って領域内の点を変位させる.デフォルトで,大小両方の変位が見えるように変位のサイズは自動的にスケールされる.デフォルトで,変位領域は変位の大きさに従って彩色される.
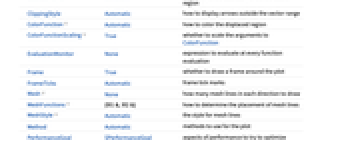
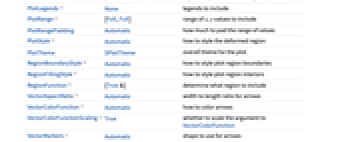
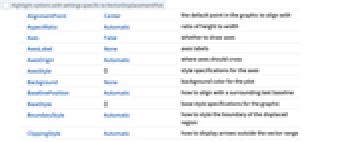
- VectorDisplacementPlotにはGraphicsと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
- デフォルトで,変位プロットはもとの領域と変位領域の表現を表示する.
- RegionBoundaryStyleおよびRegionFillingStyleを使ってもとの領域のスタイルを変えることができる.
- 次は,変位矢印を表示するVectorPointsのその他の設定である.
-
Automatic 自動選択された点 "Boundary" reg の境界に沿った点 - デフォルトで,変位矢印はもとの領域内の位置と対応する変位領域内の位置を接続する.
- VectorSizesFullはスケールされた表現ではなく完全な変位を表示する.
全オプションのリスト

例題
すべて開く すべて閉じる例 (5)
スコープ (19)
サンプリング (12)
参照領域と変形領域を比較することでスケールされた変位場を可視化する:
ベクトルは参照領域内の点から対応する(スケールされた)変形領域内の点まで描かれる:
領域はImplicitRegionでもよい:
領域はParametricRegionでもよい:
領域はMeshRegionでもよい:
領域はBoundaryMeshRegionでもよい:
プレゼンテーション (7)
オプション (64)
AspectRatio (2)
BoundaryStyle (3)
ColorFunction (4)
ColorFunctionScaling (2)
Mesh (6)
Meshを指定して変位を可視化する:
PlotRange (3)
PlotStyle (4)
RegionFunction (1)
RegionFunctionを使って参照領域を指定する:
VectorColorFunction (3)
デフォルトで,VectorColorFunctionがAutomaticならVectorColorFunctionはColorFunctionとマッチする:
ColorFunctionとは異なるVectorColorFunctionを指定する:
VectorColorFunctionは使わない:
VectorPoints (9)
VectorSizes (4)
VectorStyle (1)
VectorColorFunctionはVectorStyleよりも優先される:
アプリケーション (24)
基本的なアプリケーション (16)
非常に小さい変位と非常に大きい変位の両方が見えるように,変位は自動的にスケールされる点に注意のこと:
VectorSizesFullを使って変位の実際のサイズを表示する:
固有値と固有ベクトルの可視化 (1)
固体力学 (5)
長さ![]() ,高さ
,高さ![]() で両端が大きさ
で両端が大きさ ![]() のモーメントに従う線形弾性棒について考える:
のモーメントに従う線形弾性棒について考える:
ヤング(Young)率とポアソン(Poisson)比を指定する:
エラスティカは,細く弾性があり伸びることなく曲がる棒である.最初はまっすぐで![]() にある底部が固定され,上端にエラスティカの荷重された端を地面と平行にするのに十分な重さが加えられた垂直エラスティカについて考える.ヤコブ・ベルヌーイ(Jacob Bernoulli)によると弧の長さは以下で与えられる:
にある底部が固定され,上端にエラスティカの荷重された端を地面と平行にするのに十分な重さが加えられた垂直エラスティカについて考える.ヤコブ・ベルヌーイ(Jacob Bernoulli)によると弧の長さは以下で与えられる:
同様に,変形されたエラスティカの点の高さは以下で与えられる:
変形されていないエラスティカのParametricRegionを作成する:
無限で線形弾性があり原点に半径 ![]() の穴があって水平方向に均一な引張荷重がかけられた薄い板について考える:
の穴があって水平方向に均一な引張荷重がかけられた薄い板について考える:
平面応力の状態を仮定して,水平および垂直の変位(![]() )と(
)と(![]() )を計算する:
)を計算する:
変形された固体領域をプロットし,無次元フープ応力で彩色する.応力が穴の上下に集中している点に注目のこと:
適用された荷重の大きさにかかわらず,応力の集中係数は3である:
底部が固定され上部右辺に一様の引張荷重がかかったL字型の領域を定義する:
変形領域をプロットする.より見やすくするために変位が増幅されている点に注意のこと:
この例では,荷重の増加につれて起こる連続的な変形について考える.
![]() (赤)で固定され,
(赤)で固定され, ![]() (青)に可変垂直牽引が加えられた細いクォーターアークについて考える:
(青)に可変垂直牽引が加えられた細いクォーターアークについて考える:
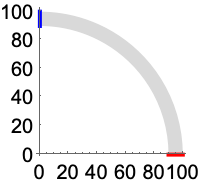
平面応力の状態を仮定して変位変数と材料パラメータを定義する:
0から最大値までのすべての荷重に適用される応力について色関数を作成する:
一連の荷重値による変形を計算して可視化する.その際,せん断応力を使って変形されたアーチに彩色する:
以下の画像をクリックして荷重を変える.アーチが細いために変位が大きく色は荷重の値すべてに対して一貫している点に注意のこと:
特性と関係 (9)
ListVectorDisplacementPlotを使って変位場データに基づいて変形を可視化する:
VectorDisplacementPlot3Dを使って変位ベクトル場に関連付けられた3D領域の変形を可視化する:
ListVectorDisplacementPlot3Dを使って同じ変形をデータに基づいて可視化する:
VectorPlotを使ってベクトル場を直接プロットする:
StreamPlotでベクトルの代りに流線を使ってプロットする:
ListVectorPlotまたはListStreamPlotをデータのプロットに使う:
VectorDensityPlotを使ってスカラー場の密度プロットを加える:
StreamDensityPlotを使ってベクトルの代りに流線をプロットする:
ListVectorDensityPlotまたはListStreamDensityPlotをデータのプロットに使う:
LineIntegralConvolutionPlotを使ってベクトル場の線積分のたたみ込みをプロットする:
VectorPlot3DとStreamPlot3Dを使って3Dベクトル場を可視化する:
ListVectorPlot3DまたはListStreamPlot3Dを使ってデータでプロットする:
SliceVectorPlot3Dで曲面上にベクトルをプロットする:
ListSliceVectorPlot3Dを使ってデータでプロットする:
ComplexVectorPlotまたはComplexStreamPlotを使って複素変数の複素関数をベクトル場としてまたは流線で可視化する:
GeoVectorPlotを使って地図上にベクトルをプロットする:
GeoStreamPlotを使ってベクトルの代りに流線をプロットする:
関連するガイド
-
▪
- ベクトルの可視化
テキスト
Wolfram Research (2021), VectorDisplacementPlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/VectorDisplacementPlot.html.
CMS
Wolfram Language. 2021. "VectorDisplacementPlot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VectorDisplacementPlot.html.
APA
Wolfram Language. (2021). VectorDisplacementPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VectorDisplacementPlot.html
BibTeX
@misc{reference.wolfram_2025_vectordisplacementplot, author="Wolfram Research", title="{VectorDisplacementPlot}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/VectorDisplacementPlot.html}", note=[Accessed: 08-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_vectordisplacementplot, organization={Wolfram Research}, title={VectorDisplacementPlot}, year={2021}, url={https://reference.wolfram.com/language/ref/VectorDisplacementPlot.html}, note=[Accessed: 08-February-2026]}