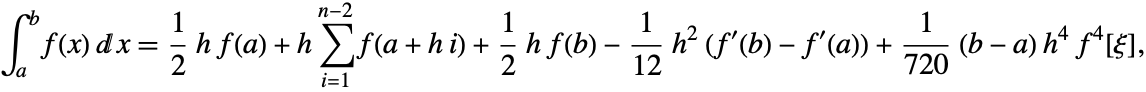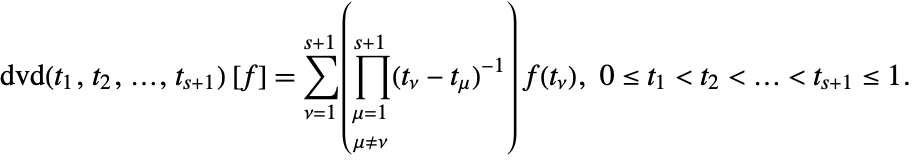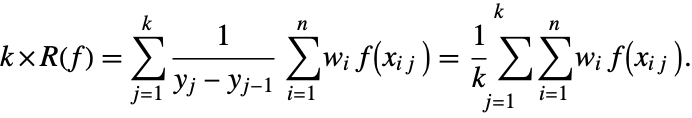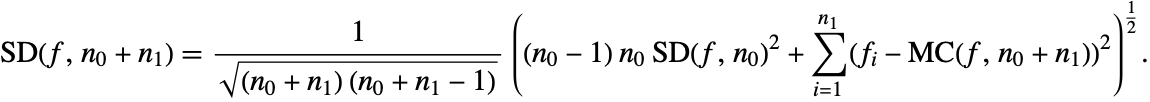NIntegrate Integration Rules
Introduction
An integration rule computes an estimate of an integral over a region, typically using a weighted sum. In the context of NIntegrate usage, an integration rule object provides both an integral estimate and an error estimate as a measure of the integral estimate's accuracy.
The following general notes pertain to weighted sum type integration rules such as "GaussKronrodRule" and "MultidimensionalRule". A separate discussion applies to other types of rules such as "LevinRule".
An integration rule samples the integrand at a set of points, called sampling points. In the literature these are also called abscissas. Corresponding to each sampling point ![]() there is a weight number
there is a weight number ![]() . An integration rule estimates the integral
. An integration rule estimates the integral ![]() with the weighted sum
with the weighted sum ![]() . An integration rule is a functional, that is, it maps functions over the interval
. An integration rule is a functional, that is, it maps functions over the interval ![]() (or a more general region) into real numbers.
(or a more general region) into real numbers.
If a rule is applied over the region ![]() this will be denoted as
this will be denoted as ![]() , where
, where ![]() is the integrand.
is the integrand.
The sampling points of the rules considered below are chosen to compute estimates for integrals either over the interval ![]() , or the unit cube
, or the unit cube ![]() , or the "centered" unit cube
, or the "centered" unit cube ![]() , where
, where ![]() is the dimension of the integral. So if
is the dimension of the integral. So if ![]() is one of these regions,
is one of these regions, ![]() will be used instead of
will be used instead of ![]() . When these rules are applied to other regions, their abscissas and estimates need to be scaled accordingly.
. When these rules are applied to other regions, their abscissas and estimates need to be scaled accordingly.
The integration rule ![]() is said to be exact for the function
is said to be exact for the function ![]() if
if ![]() .
.
The application of an integration rule ![]() to a function
to a function ![]() will be referred as an integration of
will be referred as an integration of ![]() , for example, "when
, for example, "when ![]() is integrated by
is integrated by ![]() , we get
, we get ![]() ."
."
A one-dimensional integration rule is said to be of degree ![]() if it integrates exactly all polynomials of degree
if it integrates exactly all polynomials of degree ![]() or less, and will fail to do so for at least one polynomial of degree
or less, and will fail to do so for at least one polynomial of degree ![]() .
.
A multidimensional integration rule is said to be of degree ![]() if it integrates exactly all monomials of degree
if it integrates exactly all monomials of degree ![]() or less, and will fail to do so for at least one monomial of degree
or less, and will fail to do so for at least one monomial of degree ![]() , that is, the rule is exact for all monomials of the form
, that is, the rule is exact for all monomials of the form ![]() , where
, where ![]() is the dimension,
is the dimension, ![]() , and
, and ![]() .
.
A null rule of degree ![]() will integrate to zero all monomials of degree
will integrate to zero all monomials of degree ![]() and will fail to do so for at least one monomial of degree
and will fail to do so for at least one monomial of degree ![]() . Each null rule may be thought of as the difference between a basic integration rule and an appropriate integration rule of a lower degree.
. Each null rule may be thought of as the difference between a basic integration rule and an appropriate integration rule of a lower degree.
If the set of sampling points of a rule ![]() of degree
of degree ![]() contains the set of sampling points of a rule
contains the set of sampling points of a rule ![]() of a lower degree
of a lower degree ![]() , that is,
, that is, ![]() , then
, then ![]() is said to be embedded in
is said to be embedded in ![]() . This will be denoted as
. This will be denoted as ![]() .
.
An integration rule of degree ![]() that is a member of a family of rules with a common derivation and properties but different degrees will be denoted as
that is a member of a family of rules with a common derivation and properties but different degrees will be denoted as ![]() , where
, where ![]() might be chosen to identify the family. (For example, trapezoidal rule of degree 4 might be referred to as
might be chosen to identify the family. (For example, trapezoidal rule of degree 4 might be referred to as ![]() .)
.)
If each rule in a family is embedded in another rule in the same family, then the rules of that family are called progressive. (For any given ![]() there exists
there exists ![]() , for which
, for which ![]() ).
).
An integration rule is of open type if the integrand is not evaluated at the end points of the interval. It is of closed type if it uses integrand evaluations at the interval end points.
An NIntegrate integration rule object has one integration rule for the integral estimate and one or several null rules for the error estimate. The sampling points of the integration rule and the null rules coincide. It should be clear from the context whether "integration rule" or "rule" would mean an NIntegrate integration rule object, or an integration rule in the usual mathematical sense.
Integration Rule Specification
All integration rules described below, except "MonteCarloRule", are to be used by the adaptive strategies of NIntegrate. In NIntegrate, all Monte Carlo strategies, crude and adaptive, use "MonteCarloRule".
Changing the integration rule component of an integration strategy will make a different integration algorithm.
The way to specify what integration rule the adaptive strategies in NIntegrate (see "Global Adaptive Strategy" and "Local Adaptive Strategy") should use is through a Method suboption.
If NIntegrate is given a method option that has only an integration rule specification (other than "MonteCarloRule"), then that rule is used with the "GlobalAdaptive" strategy. The two inputs below are equivalent.
For "MonteCarloRule", the adaptive Monte Carlo strategy is automatically used. The following two commands are equivalent.
"TrapezoidalRule"
The trapezoidal rule for integral estimation is one of the simplest and oldest rules (possibly used by the Babylonians and certainly by the ancient Greek mathematicians):
The compounded trapezoidal rule is a Riemann sum of the form
If the Method option is given the value "TrapezoidalRule", the compounded trapezoidal rule is used to estimate each subinterval formed by the integration strategy.
option name | default value | |
| "Points" | 5 | number of coarse trapezoidal points |
| "RombergQuadrature" | True | should Romberg quadrature be used or not |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic preprocessing |
The trapezoidal rule and its compounded (multipanel) extension are not very accurate. (The compounded trapezoidal rule is exact for linear functions and converges at least as fast as ![]() , if the integrand has continuous second derivative [DavRab84].) The accuracy of the multipanel trapezoidal rule can be increased using the Romberg quadrature.
, if the integrand has continuous second derivative [DavRab84].) The accuracy of the multipanel trapezoidal rule can be increased using the Romberg quadrature.
Since the abscissas of ![]() are a subset of
are a subset of ![]() , the difference
, the difference ![]() , can be taken to be an error estimate of the integral estimate
, can be taken to be an error estimate of the integral estimate ![]() , and can be computed without extra integrand evaluations.
, and can be computed without extra integrand evaluations.
The option "Points"->k can be used to specify how many coarse points are used. The total number of points used by "TrapezoidalRule" is ![]() .
.
"TrapezoidalRule" can be used for multidimensional integrals too.
Remark: NIntegrate has both a trapezoidal rule and a trapezoidal strategy; see "'Trapezoidal Strategy" in the tutorial "Integration Strategies". All internally implemented integration rules of NIntegrate have the suffix -Rule. So "TrapezoidalRule" is used to specify the trapezoidal integration rule, and "Trapezoidal" is used to specify the trapezoidal strategy.
Romberg Quadrature
The idea of the Romberg quadrature is to use a linear combination of ![]() and
and ![]() that eliminates the same order terms of truncation approximation errors of
that eliminates the same order terms of truncation approximation errors of ![]() and
and ![]() .
.
From the Euler–Maclaurin formula [DavRab84] we have
The ![]() terms of the equations above can be eliminated if the first equation is subtracted from the second equation four times. The result is
terms of the equations above can be eliminated if the first equation is subtracted from the second equation four times. The result is
"TrapezoidalRule" Sampling Points and Weights
"NewtonCotesRule"
Newton–Cotes integration formulas are formulas of interpolatory type with sampling points that are equally spaced.
option name | default value | |
| "Points" | 3 | number of coarse Newton–Cotes points |
| "Type" | Closed | type of the Newton–Cotes rule |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic preprocessing |
Let the interval of integration, ![]() , be divided into
, be divided into ![]() subintervals of equal length by the points
subintervals of equal length by the points
Then the integration formula of interpolatory type is given by
When ![]() is large, the Newton–Cotes
is large, the Newton–Cotes ![]() -point coefficients are large and are of mixed sign.
-point coefficients are large and are of mixed sign.
Since this may lead to large losses of significance by cancellation, a high-order Newton–Cotes rule must be used with caution.
"NewtonCotesRule" Sampling Points and Weights
"GaussBerntsenEspelidRule"
Gaussian quadrature uses optimal sampling points (through polynomial interpolation) to form a weighted sum of the integrand values over these points. On a subset of these sampling points a lower order quadrature rule can be made. The difference between the two rules can be used to estimate the error. Berntsen and Espelid derived error estimation rules by removing the central point of Gaussian rules with odd number of sampling points.
option name | default value | |
| "Points" | Automatic | number of Gauss points |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic preprocessing |
"GaussBerntsenEspelidRule" options.
A Gaussian rule ![]() of
of ![]() points for integrand
points for integrand ![]() is exact for polynomials of degree
is exact for polynomials of degree ![]() (i.e.,
(i.e., ![]() if
if ![]() is a polynomial of degree
is a polynomial of degree ![]() ).
).
Gaussian rules are of open type since the integrand is not evaluated at the end points of the interval. (Lobatto rules, Clenshaw–Curtis rules, and the trapezoidal rule are of closed type since they use integrand evaluations at the interval end points.)
This defines the divided differences functional [Ehrich2000]
For the Gaussian rule ![]() , with sampling points
, with sampling points ![]() , Berntsen and Espelid have derived the following error estimate functional (see [Ehrich2000])
, Berntsen and Espelid have derived the following error estimate functional (see [Ehrich2000])
(The original formula in [Ehrich2000] is for sampling points in ![]() . The formula above is for sampling points in
. The formula above is for sampling points in ![]() .)
.)
"GaussBerntsenEspelidRule" Sampling Points and Weights
The Berntsen–Espelid error weights are implemented below.
"GaussKronrodRule"
Gaussian quadrature uses optimal sampling points (through polynomial interpolation) to form a weighted sum of the integrand values over these points. The Kronrod extension of a Gaussian rule adds new sampling points in between the Gaussian points and forms a higher-order rule that reuses the Gaussian rule integrand evaluations.
option name | default value | |
| "Points" | Automatic | number of Gauss points that will be extended with Kronrod points |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic processing |
A Gaussian rule ![]() of
of ![]() points for integrand
points for integrand ![]() is exact for polynomials of degree
is exact for polynomials of degree ![]() , that is,
, that is, ![]() if
if ![]() is a polynomial of degree
is a polynomial of degree ![]() .
.
Gauss–Kronrod rules are of open type since the integrand is not evaluated at the end points of the interval.
The Kronrod extension ![]() of a Gaussian rule with
of a Gaussian rule with ![]() points
points ![]() adds
adds ![]() points to
points to ![]() and the extended rule is exact for polynomials of degree
and the extended rule is exact for polynomials of degree ![]() if
if ![]() is even, or
is even, or ![]() if
if ![]() is odd. The weights associated with a Gaussian rule change in its Kronrod extension.
is odd. The weights associated with a Gaussian rule change in its Kronrod extension.
Since the abscissas of ![]() are a subset of
are a subset of ![]() , the difference
, the difference ![]() can be taken to be an error estimate of the integral estimate
can be taken to be an error estimate of the integral estimate ![]() , and can be computed without extra integrand evaluations.
, and can be computed without extra integrand evaluations.
For an implementation description of Kronrod extensions of Gaussian rules, see [PiesBrand74].
"GaussKronrodRule" Sampling Points and Weights
The calculations below demonstrate the degree of the Gauss–Kronrod integration rule (see above).
The command below implements the integration rule weighted sums for the integral estimate, ![]() , and the error estimate,
, and the error estimate, ![]() , where
, where ![]() are the abscissas,
are the abscissas, ![]() are the weights, and
are the weights, and ![]() are the error weights.
are the error weights.
The error estimate is not zero since the embedded Gauss rule is exact for polynomials of degree ![]() . If we integrate a polynomial of that degree, the error estimate becomes zero.
. If we integrate a polynomial of that degree, the error estimate becomes zero.
"LobattoKronrodRule"
The Lobatto integration rule is a Gauss-type rule with preassigned abscissas. It uses the end points of the integration interval and optimal sampling points inside the interval to form a weighted sum of the integrand values over these points. The Kronrod extension of a Lobatto rule adds new sampling points in between the Lobatto rule points and forms a higher-order rule that reuses the Lobatto rule integrand evaluations.
option name | default value | |
| "Points" | 5 | number of Gauss–Lobatto points that will be extended with Kronrod points |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic preprocessing |
A Lobatto rule ![]() of
of ![]() points for integrand
points for integrand ![]() is exact for polynomials of degree
is exact for polynomials of degree ![]() , (i.e.,
, (i.e., ![]() if
if ![]() is a polynomial of degree
is a polynomial of degree ![]() ).
).
The Kronrod extension ![]() of a Lobatto rule with
of a Lobatto rule with ![]() points
points ![]() adds
adds ![]() points to
points to ![]() and the extended rule is exact for polynomials of degree
and the extended rule is exact for polynomials of degree ![]() if
if ![]() is even, or
is even, or ![]() if
if ![]() is odd. The weights associated with a Lobatto rule change in its Kronrod extension.
is odd. The weights associated with a Lobatto rule change in its Kronrod extension.
As with "GaussKronrodRule", the number of Gauss points is specified with the option "GaussPoints". If "LobattoKronrodRule" is invoked with "Points"->n, the total number of rule points will be ![]() .
.
Since the Lobatto rule is a closed rule, the integrand needs to be evaluated at the end points of the interval. If there is a singularity at these end points, NIntegrate will ignore it.
For an implementation description of Kronrod extensions of Lobatto rules, see [PiesBrand74].
"LobattoKronrodRule" Sampling Points and Weights
The calculations below demonstrate the degree of the Lobatto–Kronrod integration rule (see above).
The command below implements the integration rule weighted sums for the integral estimate, ![]() , and the error estimate,
, and the error estimate, ![]() , where
, where ![]() are the abscissas,
are the abscissas, ![]() are the weights, and
are the weights, and ![]() are the error weights.
are the error weights.
The preceding error estimate is not zero since the embedded Lobatto rule is exact for polynomials of degree ![]() . If we integrate a polynomial of that degree, the error estimate becomes zero.
. If we integrate a polynomial of that degree, the error estimate becomes zero.
"ClenshawCurtisRule"
A Clenshaw–Curtis rule uses sampling points derived from the Chebyshev polynomial approximation of the integrand.
option name | default value | |
| "Points" | 5 | number of coarse Clenshaw–Curtis points |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic processing |
Theoretically a Clenshaw–Curtis rule with ![]() sampling points is exact for polynomials of degree
sampling points is exact for polynomials of degree ![]() or less. In practice, though, Clenshaw–Curtis rules achieve the accuracy of the Gaussian rules [Evans93][OHaraSmith68]. The error of the Clenshaw–Curtis formula is analyzed in [OHaraSmith68].
or less. In practice, though, Clenshaw–Curtis rules achieve the accuracy of the Gaussian rules [Evans93][OHaraSmith68]. The error of the Clenshaw–Curtis formula is analyzed in [OHaraSmith68].
The sampling points of the classical Clenshaw–Curtis rule are zeros of Chebyshev polynomials. The sampling points of a practical Clenshaw–Curtis rule are chosen to be Chebyshev polynomial extremum points. The classical Clenshaw–Curtis rules are not progressive, but the practical Clenshaw–Curtis rules are [DavRab84][KrUeb98].
Let ![]() denote a practical Clenshaw–Curtis rule of
denote a practical Clenshaw–Curtis rule of ![]() sampling points for the function
sampling points for the function ![]() .
.
The progressive property means that the sampling points of ![]() are a subset of the sampling points of
are a subset of the sampling points of ![]() . Hence the difference
. Hence the difference ![]() can be taken to be an error estimate of the integral estimate
can be taken to be an error estimate of the integral estimate ![]() , and can be computed without extra integrand evaluations.
, and can be computed without extra integrand evaluations.
"ClenshawCurtisRule" Sampling Points and Weights
"MultipanelRule"
"MultipanelRule" combines into one rule the applications of a one-dimensional integration rule over two or more adjacent intervals. An application of the original rule to any of the adjacent intervals is called a panel.
option name | default value | |
| Method | "NewtonCotesRule" | integration rule specification that provides the abscissas, weights, and error weights for a single panel |
| "Panels" | 5 | number of panels |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic processing |
Let the unit interval ![]() be partitioned into
be partitioned into ![]() sub-intervals with the points
sub-intervals with the points ![]() .
.
it can be transformed into a rule for the interval ![]() ,
,
Let ![]() , and
, and ![]() ,
, ![]() . Then the
. Then the ![]() -panel integration rule based on
-panel integration rule based on ![]() can be written explicitly as
can be written explicitly as
If ![]() is closed, that is,
is closed, that is, ![]() has
has ![]() and
and ![]() as sampling points, then
as sampling points, then ![]() , and the number of sampling points of
, and the number of sampling points of ![]() can be reduced to
can be reduced to ![]() . (This is done in the implementation of "MultipanelRule".)
. (This is done in the implementation of "MultipanelRule".)
More about the theory of multipanel rules, also referred to as compounded or composite rules, can be found in [KrUeb98] and [DavRab84].
"MultipanelRule" Sampling Points and Weights
"CartesianRule"
A ![]() -dimensional Cartesian rule has sampling points that are a Cartesian product of the sampling points of
-dimensional Cartesian rule has sampling points that are a Cartesian product of the sampling points of ![]() one-dimensional rules. The weight associated with a Cartesian rule sampling point is the product of the one-dimensional rule weights that correspond to its coordinates.
one-dimensional rules. The weight associated with a Cartesian rule sampling point is the product of the one-dimensional rule weights that correspond to its coordinates.
option name | default value | |
| Method | "GaussKronrodRule" | a rule or a list of rules with which the Cartesian product rule will be formed |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic preprocessing |
For example, suppose we have the formulas:
that are exact for polynomials of degree ![]() ,
, ![]() , and
, and ![]() , respectively. Then it is not difficult to see that the formula with
, respectively. Then it is not difficult to see that the formula with ![]() points,
points,
is exact for polynomials in ![]() of degree
of degree ![]() . Note that the weight associated with the abscissa
. Note that the weight associated with the abscissa ![]() is
is ![]() .
.
The general Cartesian product formula for ![]() one-dimensional rules the
one-dimensional rules the ![]() of which has
of which has ![]() sampling points
sampling points ![]() and weights
and weights ![]() is
is
where ![]() , and for each integer
, and for each integer ![]() ,
, ![]() and
and ![]() .
.
Cartesian rules are applicable for relatively low dimensions (![]() ), since for higher dimensions they are subject to "combinatorial explosion". For example, a five-dimensional Cartesian product of
), since for higher dimensions they are subject to "combinatorial explosion". For example, a five-dimensional Cartesian product of ![]() identical one-dimensional rules each having
identical one-dimensional rules each having ![]() sampling points would have
sampling points would have ![]() sampling points.
sampling points.
NIntegrate uses Cartesian product rule if the integral is multidimensional and the Method option is given a one-dimensional rule or a list of one-dimensional rules.
More about Cartesian rules can be found in [Stroud71].
"CartesianRule" Sampling Points and Weights
NIntegrate`CartesianRuleData keeps the abscissas and the weights of each rule separated. Otherwise, as it can be seen from (3) the result might be too big for higher dimensions.
"MultidimensionalRule"
A fully symmetric integration rule for the cube ![]() ,
, ![]() consists of sets of points with the following properties: (1) all points in a set can be generated by permutations and/or sign changes of the coordinates of any fixed point from that set; (2) all points in a set have the same weight associated with them.
consists of sets of points with the following properties: (1) all points in a set can be generated by permutations and/or sign changes of the coordinates of any fixed point from that set; (2) all points in a set have the same weight associated with them.
A set of points of a fully symmetric integration rule that satisfies the preceding properties is called an orbit. A point of an orbit, ![]() , for the coordinates of which the inequality
, for the coordinates of which the inequality ![]() holds, is called a generator. (See [KrUeb98][GenzMalik83].)
holds, is called a generator. (See [KrUeb98][GenzMalik83].)
option name | default value | |
| "Generators" | 5 | number of generators of the fully symmetric rule |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic preprocessing |
"MultidimensionalRule" options.
If an integration rule has ![]() orbits denoted
orbits denoted ![]() , and the
, and the ![]() th of them,
th of them, ![]() , has a weight
, has a weight ![]() associated with it, then the integral estimate is calculated with the formula
associated with it, then the integral estimate is calculated with the formula
A null rule of degree ![]() will integrate to zero all monomials of degree
will integrate to zero all monomials of degree ![]() and will fail to do so for at least one monomial of degree
and will fail to do so for at least one monomial of degree ![]() . Each null rule may be thought of as the difference between a basic integration rule and an appropriate integration of lower degree.
. Each null rule may be thought of as the difference between a basic integration rule and an appropriate integration of lower degree.
The "MultidimensionalRule" object of NIntegrate is basically an interface to three different integration rule objects that combine an integration rule and one or several null rules. Their number of generators and orders are summarized in the table below. The rule objects with 6 and 9 generators use three null rules, each of which is a linear combination of two null rules. The null rule linear combinations are used in order to avoid phase errors. See [BerntEspGenz91] for more details about how the null rules are used.
| Number ofGenerators | Integration Rule Order | Order of Each of the Null Rules | Described in |
| 5 | 7 | 5 | [GenzMalik80] |
| 6 | 7 | 5,3,1 | [GenzMalik83][BerntEspGenz91] |
| 9 | 9 | 7,5,3 | [GenzMalik83][BerntEspGenz91] |
"MultidimensionalRule" Sampling Points and Weights
This subsection gives an example of a calculation of an integral estimate with a fully symmetric multidimensional rule.
"LevinRule"
A Levin-type rule estimates the integral of an oscillatory function by approximating the antiderivative as a product of a polynomial and the oscillatory part of the integrand.
By default, "LevinRule" automatically detects the oscillatory part of the integrand and applies the collocation method described below to form an integral estimate. Options can be used to specify the oscillatory part and to control the detailed behavior of the numerical algorithm, including whether to adaptively switch to a non-oscillatory alternative integration rule.
option name | default value | |
| "Points" | Automatic | number of coarse collocation points |
| "EndpointLimitTerms" | Automatic | polynomial extrapolation order at non-numerical endpoint |
| "TimeConstraint" | 10 | maximum time solving collocation equations per integration step |
| "MethodSwitching" | True | whether to automatically switch to non-oscillatory rule |
| "OscillationThreshold" | 10 | approximate number of oscillations above which to apply "LevinRule" |
| Method | Automatic | alternative non-oscillatory rule |
| "LevinFunctions" | Automatic | oscillatory functions to include in kernel |
| "MaxOrder" | 50 | maximum differential order of kernel |
| ExcludedForms | {} | forms to exclude from kernel |
| "AdditiveTerm" | Automatic | additive non-oscillatory part of integrand |
| "Amplitude" | Automatic | coefficients of kernel in integrand |
| "DifferentialMatrix" | Automatic | matrix form of linear ODE satisfied by kernel |
| "Kernel" | Automatic | explicit oscillatory kernel |
Levin-Type Collocation Method
Scope
Basic Levin-type methods for one-dimensional numerical integration [Levin96] apply to oscillatory integrals of the form
where the oscillatory part ![]() must satisfy a linear ordinary differential equation (linear ODE) of order
must satisfy a linear ordinary differential equation (linear ODE) of order ![]() written in matrix form as
written in matrix form as
where ![]() is one of the
is one of the ![]() . The vector of functions
. The vector of functions ![]() is the oscillatory "kernel" and the matrix
is the oscillatory "kernel" and the matrix ![]() is the "differential matrix".
is the "differential matrix".
For example, if ![]() , the oscillatory kernel may be
, the oscillatory kernel may be
Levin-type methods also handle the more general case
where in the simpler case above we typically have ![]() and
and ![]() . The vector of functions
. The vector of functions ![]() is the "amplitude".
is the "amplitude".
Most of the oscillatory special functions of mathematics, such as Exp, BesselJ, AiryAi, and so on, satisfy a linear ODE and can thus be integrated using Levin-type methods. Furthermore, any product, sum, or integer power of such functions, or their compositions with any non-rapidly oscillatory function, also satisfies a linear ODE. See also DifferentialRootReduce.
The "LevinRule" method can be applied to a slightly more general class of integrals,
where the "additive term" ![]() is handled separately by a traditional quadrature method such as "GaussKronrodRule".
is handled separately by a traditional quadrature method such as "GaussKronrodRule".
Levin-type methods are effective when the amplitude ![]() , the additive term
, the additive term ![]() , and the differential matrix
, and the differential matrix ![]() are not themselves rapidly oscillatory [Levin97].
are not themselves rapidly oscillatory [Levin97].
Collocation Method
In a Levin-type collocation method, an antiderivative of the integrand ![]() is sought of the form
is sought of the form ![]() for some unknown functions
for some unknown functions ![]() :
:
Differentiating both sides with respect to ![]() , and using
, and using ![]() , we find that all of the
, we find that all of the ![]() cancel, and the functions
cancel, and the functions ![]() satisfy the non-oscillatory differential equations
satisfy the non-oscillatory differential equations
These equations can be solved for the ![]() using a collocation method in which we approximate each
using a collocation method in which we approximate each ![]() as a linear combination of some simple set of
as a linear combination of some simple set of ![]() predetermined basis functions
predetermined basis functions ![]() :
:
In "LevinRule", the basis functions ![]() are chosen to be Chebyshev polynomials ChebyshevT[k,x]. Substituting this into the differential equations for
are chosen to be Chebyshev polynomials ChebyshevT[k,x]. Substituting this into the differential equations for ![]() yields
yields ![]() linear equations for the
linear equations for the ![]() collocation coefficients
collocation coefficients ![]() :
:
Since ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are all known functions, we can evaluate these linear equations at
are all known functions, we can evaluate these linear equations at ![]() collocation nodes
collocation nodes ![]() inside the integration range. This yields
inside the integration range. This yields ![]() linear equations for the
linear equations for the ![]() coefficients
coefficients ![]() . Upon solving these equations numerically, we have an approximate form for the
. Upon solving these equations numerically, we have an approximate form for the ![]() , and we may directly evaluate the integral using the fundamental theorem of calculus, as
, and we may directly evaluate the integral using the fundamental theorem of calculus, as
NIntegrate uses the abscissae of the corresponding "GaussKronrodRule" as the collocation nodes ![]() .
.
"LevinRule" computes the integral estimate using ![]() collocation nodes where
collocation nodes where ![]() is the value of the "Points" method option. A lower order integral estimate is also computed using every second collocation node (
is the value of the "Points" method option. A lower order integral estimate is also computed using every second collocation node (![]() ). The difference between these two integral estimates is taken as an estimate of the error of the algorithm.
). The difference between these two integral estimates is taken as an estimate of the error of the algorithm.
Specifying Oscillatory Kernel
By default, "LevinRule" automatically selects an oscillatory kernel comprising as much of the integrand as possible. This behavior can be modified in detail with options.
If the integrand contains an oscillatory function that is not highly oscillatory over the integration region, it may be more efficient to exclude it from the oscillatory kernel. For example, Sin[x] is not highly oscillatory over the region {x,0,5}.
The "Kernel" method option can be used to specify the oscillatory part the integrand.
The "ExcludedForms" method option can be used to specify parts of the integrand that should not be included in the automatically detected oscillatory kernel.
The "LevinFunctions" method option can be used to specify which types of functions should be included in the automatically detected oscillatory kernel. The setting "LevinFunctions"->{h1,h2,…} detects only the specific functions hi.
The setting "LevinFunctions"->{grp1,grp2,…} detects functions from the named groups grpi.
| "ExpRelated" | Exp, Power |
| "TrigRelated" | Sin, Cos, Sinh, Cosh, Haversine, Sinc |
| "ErfRelated" | Erf, Erfc, Erfi |
| "TrigIntegrals" | FresnelS, FresnelC, SinIntegral, CosIntegral, SinhIntegral, CoshIntegral |
| "BesselRelated" | BesselJ, BesselY, HankelH1, BesselI, BesselK, HankelH2, StruveH, StruveL, SphericalBesselJ |
| "AiryRelated" | AiryAi, AiryAiPrime, AiryBi, AiryBiPrime |
| "HypergeometricRelated" | HypergeometricPFQ, HypergeometricPFQRegularized, Hypergeometric0F1, Hypergeometric0F1Regularized, Hypergeometric2F1, Hypergeometric2F1Regularized |
| "InverseTrig" | ArcSin, ArcCos, ArcSinh, ArcCosh, ArcSec, ArcCsc, ArcSech, ArcCsch, ArcTan, ArcCot, ArcTanh, ArcCoth, InverseHaversine |
| "Elliptic" | EllipticE, EllipticK |
| "GammaRelated" | Gamma, GammaRegularized, Beta, BetaRegularized |
| "ExpIntegrals" | ExpIntegralE, ExpIntegralEi, DawsonF |
| "DifferentialRoots" | DifferentialRoot objects |
| "Other" | Log |
Named groups recognized by the "LevinFunctions" method option.
By default, the setting for "LevinFunctions" includes all named groups apart from "Other", "InverseTrig", and "Elliptic". This setting corresponds to elementary and special functions that are oscillatory in some part of their domain.
NIntegrate`LevinIntegrand Object
It is possible to inspect in detail the oscillatory kernel, differential matrix, amplitude, and additive term detected by NIntegrate using the internal function NIntegrate`LevinIntegrandReduce. NIntegrate`LevinIntegrandReduce returns an NIntegrate`LevinIntegrand object representing a fully processed integrand to which a Levin-type collocation method can be applied.
Properties of an NIntegrate`LevinIntegrand object li are accessed using the form li["prop"].
The "Rules" property gives the main properties of the NIntegrate`LevinIntegrand that are used in the Levin-type collocation algorithm.
Using this property we can quickly see the effect of different "LevinRule" method options on the oscillatory kernel detection, such as the "AdditiveTerm" option.
We can see how to use the "LevinFunctions" option to include or exclude groups of functions from the integrand.
It is possible to completely specify all four parts of the integrand decomposition (additive term, amplitude, kernel, and differential matrix). This can be used for efficient multiple calls to NIntegrate with similar integrands.
Note that, in this case, the first argument to NIntegrate is completely ignored.
"MonteCarloRule"
A Monte Carlo rule estimates an integral by forming a uniformly weighted sum of integrand evaluations over random (quasi-random) sampling points.
option name | default value | |
| "Points" | 100 | number of sampling points |
| "PointGenerator" | Random | sampling points coordinates generator |
| "AxisSelector" | Automatic | selection algorithm of the splitting axis when global adaptive Monte Carlo integration is used |
| "SymbolicProcessing" | Automatic | number of seconds to do symbolic preprocessing |
In Monte Carlo methods [KrUeb98], the ![]() -dimensional integral
-dimensional integral ![]() is interpreted as the following expected (mean) value
is interpreted as the following expected (mean) value
where ![]() is the mean value of the function
is the mean value of the function ![]() interpreted as a random variable, with respect to the uniform distribution on
interpreted as a random variable, with respect to the uniform distribution on ![]() , that is, the distribution with probability density
, that is, the distribution with probability density ![]() .
. ![]() denotes the characteristic function of the region
denotes the characteristic function of the region ![]() ;
; ![]() denotes the volume of
denotes the volume of ![]() .
.
The crude Monte Carlo estimate of the expected value ![]() is obtained by taking
is obtained by taking ![]() independent random vectors
independent random vectors ![]() with density
with density ![]() (that is, the vectors are uniformly distributed on
(that is, the vectors are uniformly distributed on ![]() ), and making the estimate
), and making the estimate
Remark: The function ![]() is a valid probability density function because it is non-negative on the whole of
is a valid probability density function because it is non-negative on the whole of ![]() and
and ![]() .
.
According to the strong law of large numbers, the convergence
happens with probability ![]() . The strong law of large numbers does not provide information for the error
. The strong law of large numbers does not provide information for the error ![]() , so a probabilistic estimate is used.
, so a probabilistic estimate is used.
Formula (5) is an unbiased estimator of ![]() (that is, the expectation of
(that is, the expectation of ![]() for various sets of
for various sets of ![]() is
is ![]() ) and its variance is
) and its variance is
where ![]() denotes the variance of
denotes the variance of ![]() . The standard error of
. The standard error of ![]() is thus
is thus ![]() .
.
In practice the ![]() is not known, so it is estimated with the formula
is not known, so it is estimated with the formula
The result of the Monte Carlo estimation can be written as ![]() .
.
It can be seen from Equation (6) that the convergence rate of the crude Monte Carlo estimation does not depend on the dimension ![]() of the integral, and if
of the integral, and if ![]() sampling points are used then the convergence rate is
sampling points are used then the convergence rate is ![]() .
.
The NIntegrate integration rule "MonteCarloRule" calculates the estimates ![]() and
and ![]() .
.
The estimates can be improved incrementally. That is, if we have the estimates ![]() and
and ![]() , and a new additional set of sample function values
, and a new additional set of sample function values ![]() , then using (7) and (8) we have
, then using (7) and (8) we have
To compute the estimates ![]() and
and ![]() , it is not necessary to know the random points used to compute the estimates
, it is not necessary to know the random points used to compute the estimates ![]() and
and ![]() .
.
"AxisSelector"
When used for multidimensional global adaptive integration, "MonteCarloRule" chooses the splitting axis of an integration subregion it is applied to in two ways: (i) by random selection or (ii) by minimizing the sum of the variances of the integral estimates of each half of the subregion, if the subregion is divided along that axis. The splitting axis is selected after the integral estimation.
The random axis selection is done in the following way. "MonteCarloRule" keeps a set of axes for selection, ![]() . Initially
. Initially ![]() contains all axes. An element of
contains all axes. An element of ![]() is randomly selected. The selected axis is excluded from
is randomly selected. The selected axis is excluded from ![]() . After the next integral estimation, an axis is selected from
. After the next integral estimation, an axis is selected from ![]() and excluded from it, and so forth. If
and excluded from it, and so forth. If ![]() is empty, it is filled up with all axes.
is empty, it is filled up with all axes.
The minimization of variance axis selection is done in the following way. During the integration over the region, a subset of the sampling points and their integrand values is stored. Then for each axis, the variances of the two subregions that the splitting along this axis will produce are estimated using the stored sampling point and corresponding integrand values. The axis for which the sum of these variances is minimal is chosen to be the splitting axis, since this would mean that if the region is split on that axis, the new integration error estimate will be minimal. If it happens that for some axis all stored points are clustered in one of the half-regions, then that axis is selected for splitting.
option value | |
| Random | random splitting axis election |
| MinVariance{MinVariance, "SubsampleFraction"->frac} | splitting axis selection that minimizes the sum of variances of the new regions |
option name | default value | |
| "SubsampleFraction" | 1/10 | fraction of the sampling points used to determine the splitting axis |
In the examples below the two axis selection algorithms are compared. In general, the minimization of variance selection uses less number of sampling points. Nevertheless, using the minimization of variance axis selection slows down the application of "MonteCarloRule". So for integrals for which both axis selection methods would result in the same number of sampling points, it is faster to use random axis selection. Also, using larger fraction sampling points to determine the splitting axis in minimization of variance selection makes the integration slower.
Comparisons of the Rules
All integration rules, except "MonteCarloRule", are to be used by adaptive strategies in NIntegrate. Changing the type and the number of points of the integration rule component for an integration strategy will make a different integration algorithm. In general these different integration algorithms will perform differently for different integrals. Naturally the following questions arise.
1. Is there a type of rule that is better than other types for any integral or for integrals of a certain type?
2. Given an integration strategy, what rules perform better with it? For what integrals?
3. Given an integral, an integration strategy, and an integration rule, what number of points in the rule will minimize the total number of sampling points used to reach an integral estimate that satisfies the precision goal?
For a given integral and integration strategy the integration rule which achieves a result that satisfies the precision goal with the smallest number of sampling points is called the best integration rule. There are several factors that determine the best integration rule.
4. In general the higher the degree of the rule the faster the integration will be for smooth integrands and for higher-precision goals. On the other hand, the rule degree might be too high for the integrand and hence too many sampling points might be used when the adaptive strategies work around, for example, the integrand's discontinuities.
5. The error estimation functional of a rule influences significantly the total amount of work by the integration strategy. Rules with a smaller number of points might lead (1) to a wrong result because of underestimation of the integral, or (2) to applying too many sampling points because of overestimation of the integrand. (See "Examples of Pathological Behavior".) Further, the error estimation functional might be computed with one or several embedded null rules. In general, the larger the number of the null rules the better the error estimation—fewer phase errors are expected. The number of the null rules and the weights assigned to them in the sum that computes the error estimate determine the sets of pathological integrals and integrals hard to compute for that rule. (Some of the multidimensional rules of NIntegrate use several embedded null rules to compute the error estimate. All of the one-dimensional integration rules of NIntegrate use only one null rule.)
6. Local adaptive strategies are more effective with closed rules that have their sampling points more uniformly distributed (for example, "ClenshawCurtisRule") than with open rules (for example, GaussKronrodRule) and closed rules that have sampling points distributed in a non-uniform way (for example, "LobattoKronrodRule").
7. The percent of points reused by the strategy might greatly determine what is the best rule. For one-dimensional integrals, "LocalAdaptive" reuses all points of the closed rules. "GlobalAdaptive" throws away almost all points of the regions that need improvement of their error estimate.
Number of Points in a Rule
This subsection demonstrates with examples that the higher the degree of the rule the faster the integration will be for smooth integrands and for higher-precision goals. It also shows examples in which the degree of the rule is too high for the integrand and hence too many sampling points are used when the adaptive strategies work around the integrand's discontinuities. All examples use Gaussian rules with Berntsen–Espelid error estimate.
Here is the error of a Gaussian rule in the interval ![]() .
.
(See [DavRab84].)
Minimal Number of Sampling Points
Rule Comparison
Examples of Pathological Behavior
Tricking the Error Estimator
In this subsection an integral will be discussed which NIntegrate underestimates with its default settings since it fails to detect part of the integrand. The part is detected if the precision goal is increased.
The Wrong Estimation
Better Results
Why the Estimator Is Misled
It can be seen on the preceding plot that NIntegrate does extensive computation around the top of the second spike near ![]() . NIntegrate does not do as much computation around the unintegrated spike near
. NIntegrate does not do as much computation around the unintegrated spike near ![]() .
.
Since the difference is the error estimate assigned for the region ![]() , with the default precision goal NIntegrate never picks it up for further integration refinement.
, with the default precision goal NIntegrate never picks it up for further integration refinement.
Phase Errors
In this subsection are discussed causes why integration rules might seriously underestimate or overestimate the actual error of their integral estimates. Similar discussion is given in [LynKag76].
(Note that NIntegrate gives correct results for higher-precision goals.)
Below is an explanation why this happens.
Let the integration rule ![]() be embedded in the rule
be embedded in the rule ![]() . Accidentally, the error estimate
. Accidentally, the error estimate ![]() of the integral estimate
of the integral estimate ![]() , where
, where ![]() , can be too small compared with the exact error
, can be too small compared with the exact error ![]() .
.
In the plot above, the blue graph is for the estimated error, ![]() . The graph of the actual error
. The graph of the actual error ![]() is red.
is red.
You can see that the value 0.415 of the parameter ![]() is very close to one of the
is very close to one of the ![]() local minimals.
local minimals.
A one-dimensional quadrature rule can be seen as the result of the integration of a polynomial that is fitted through the rule's abscissas and the integrand values over them. We can further try to see the actual fitting polynomials for the integration of f[x,λ,μ].
In the plots below the function f[x,λ,μ] is plotted in red, the Gauss polynomial is plotted in blue, the Gauss–Kronrod polynomial is plotted in violet, the Gauss sampling points are in black, and the Gauss–Kronrod sampling points are in red.
You can see that since the peak of f[x,0.415,1.25] falls approximately halfway between two abscissas, its approximation is an underestimate.
Conversely, you can see that since the peak of f[x,0.53,1.25] falls approximately on one of the abscissas, its approximation is an overestimate.
Index of Technical Terms
Degree of a one-dimensional integration rule