DistributionFitTest

DistributionFitTest[data]

data が正規分布に従っているかどうかの検定を行う．

DistributionFitTest[data,dist]

data が dist に従った分布かどうかの検定を行う．

DistributionFitTest[data,dist,"property"]

"property"の値を返す．

詳細とオプション

  • DistributionFitTestは data が分布 dist の母集団から得られたという帰無仮説 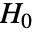およびそうではないという対立仮説 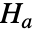で適合度仮説検定を実行する．
  • デフォルトで，確率値つまり 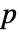値が返される．
  • 小さい 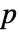値は data が dist から来ている可能性が低いことを示す．
  • dist は，記号または数値の母数，またはデータ集合，を持つ任意の記号分布でよい．
  • data は一変量{x1,x2,…}でも多変量{{x1,y1,…},{x2,y2,…},…}でもよい．
  • DistributionFitTest[data,dist,Automatic]は一般的な対立仮説に対して data と dist に当て嵌まる最も強力な検定を選ぶ．
  • DistributionFitTest[data,dist,All]は data と dist に適用されるすべての検定を選ぶ．
  • DistributionFitTest[data,dist,"test"]は"test"に従って 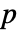値をレポートする．
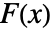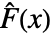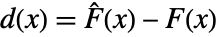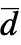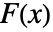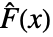  • 多くの検定が，検定分布 dist の累積分布関数 ，データの経験的累積分布関数 ，それらの差分 と =Expectation[d(x),…]を使う．累積分布関数である と は帰無仮説 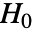下で同じでなければならない．
  • 次の検定は一変量分布と多変量分布に使える．
  • "AndersonDarling"分布，データExpectation[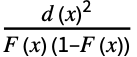]に基づく
    "CramerVonMises"分布，データExpectation[d(x)2]に基づく
    "JarqueBeraALM"正規性歪度と尖度に基づく
    "KolmogorovSmirnov"分布，データsup_x TemplateBox[{{d, (, x, )}}, Abs]に基づく
    "Kuiper"分布，データ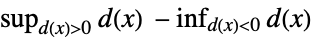に基づく
    "PearsonChiSquare"連続，データ期待ヒストグラムと観察ヒストグラムに基づく
    "ShapiroWilk"正規性変位値に基づく
    "WatsonUSquare"分布，データExpectation[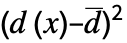]に基づく
  • 次の検定は多変量分布に使用できる．
  • "BaringhausHenze"正規性経験的特性関数に基づく
    "DistanceToBoundary"一様性一様境界までの距離に基づく
    "MardiaCombined"正規性Mardia歪度とMardia尖度の組合せ
    "MardiaKurtosis"正規性多変量の尖度に基づく
    "MardiaSkewness"正規性多変量の歪度に基づく
    "SzekelyEnergy"データNewtonのポテンシャルエネルギーに基づく
  • DistributionFitTest[data,dist,"property"]を使って"property"の値を直接与えることができる．
  • 検定結果のレポートに関連する特性
  • "AllTests"適用可能なすべての検定のリスト
    "AutomaticTest"Automaticが使われた場合に選ばれる検定
    "DegreesOfFreedom"検定で使われる自由度
    "PValue" 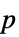値のリスト
    "PValueTable" 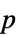値のフォーマットされた表
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計量と 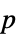値のペアのリスト
    "TestDataTable" 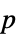値と検定統計量のフォーマットされた表
    "TestStatistic"検定統計量のリスト
    "TestStatisticTable"検定統計量のフォーマットされた表
    "HypothesisTestData"HypothesisTestDataオブジェクトを返す
  • DistributionFitTest[data,dist,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．このオブジェクトを使って，追加的な検定結果と htd["property"]の形式で特性を取り出すことができる．
  • データ分布に関連する特性
  • "FittedDistribution"データのフィットした分布
    "FittedDistributionParameters"データの分布母数
  • 使用可能なオプション
  • Method Automatic 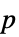値をの計算に使用するメソッド
    SignificanceLevel 0.05診断とレポートのための切捨て
  • 適合度検定では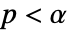， のときにのみ 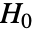が棄却されるような切捨て 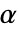が選択される．特性"TestConclusion"および"ShortTestConclusion"で使われる 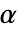の値はSignificanceLevelオプションで制御される．デフォルトの 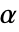は0.05である．
  • Method->"MonteCarlo"の設定では，入力 siと同じ長さの 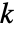個のデータ集合が 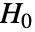のもとにフィットされた分布を使って生成される．次に，DistributionFitTest[si,dist,{"TestStatistic",test}]からのEmpiricalDistributionを使って 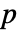値が推定される．

例題

すべて開くすべて閉じる

例  (3)

正規性についてデータの検定を行う：

さらに特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

完全な検定表：

データのヒストグラムを検定分布の確率密度関数と比較する：

データ集合の特定の分布へのフィットを検定する：

Anderson–Darling検定表を抽出する：

検定結果をProbabilityPlotで証明する：

多変量分布への適合度を調べるために，データを検定する：

検定分布の周辺確率密度関数をデータに対してプロットし，検定結果を確認する：

スコープ  (22)

検定  (16)

正規性についてデータの検定を行う：

正規分布に従うデータの 値は大抵の場合大きい：

正規分布に従わないデータの 値は大抵の場合小さい：

第3引数をAutomaticに指定して，一般に検出力が高く適切な検定を適用する：

特性"AutomaticTest"はどの検定を選択したかを知るのに使われる：

データが特定の分布にフィットするかどうかの検定を行う：

WeibullDistribution[1,2]に対するよいフィットを棄却するための十分な証拠はない：

派生分布への適合度を検定する：

値は混合から得られたのではないデータに比べて混合データの場合には大きい：

数量データについて適合度の検定を行う：

正規性をチェックする：

特定の分布についての適合度をチェックする：

式に基づいた分布への適合度を検定する：

母数を指定しないとその母数はデータから推定される：

値はどの母数が推定されたかに依存する：

多変量の正規性についてデータの検定を行う：

正規分布に従うデータの 値は，一般に，正規分布には従わないデータのそれよりも大きい：

特定の多変量分布への適合度についてデータの検定を行う：

MultinormalDistributionと多変量のUniformDistributionの検定をそれぞれ行う：

2つのデータ集合の分布を比較する：

サンプルサイズは同じではなくてもよい：

2つの多変量データ集合の分布を比較する：

同じ分布に従うデータ間の 値は異なる分布に従うデータ間のそれよりも大きい：

特定の適合度検定を行う：

任意の数の検定を同時に行うことができる：

データと分布に適したすべての検定を同時に行う：

特性"AllTests"を使ってどの検定が使われたかを調べる：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出可能な特性：

HypothesisTestDataオブジェクトからいくつかの特性を抽出する：

Cramér–von Mises検定からの 値と検定統計量：

任意の数の特性を同時に抽出する：

Anderson–Darling 値と検定統計量からの結果：

データ特性  (2)

母数が指定されていない場合のフィットされた分布を得る：

フィットされた分布から母数を抽出する：

フィットされた分布の確率密度関数をデータに対してプロットする：

フィットを適合度検定で確認する：

母数が指定されていると検定分布が返される：

データとフィットされた分布を視覚的に比較する：

レポート  (4)

いくつかの検定を選択して使い，結果を一覧にする：

すべての適切な検定結果を示す完全な表：

選択された検定結果の表：

特化したレポートのために検定表から項目を取り出す：

値は0.05よりも大きいので，正規性を棄却するための証拠はこのレベルでは見当たらない：

1つあるいは複数の検定の 値を表にする：

表からの 値：

すべての適切な検定からの 値の表：

検定の部分集合からの 値の表：

1つあるいは複数の検定からの検定統計量をレポートする：

表からの検定統計量：

すべての適切な検定からの検定統計量の表：

オプション  (6)

Method  (4)

モンテカルロに基づいたメソッドを使うか，最速メソッドを自動的に選ぶかする：

モンテカルロに基づいたメソッドに使うサンプル数を設定する：

モンテカルロ推定ではサンプル数を増すと真の 値に収束する：

モンテカルロに基づくメソッドで使われるランダムなシードを設定する：

このシードは生成器の状態に影響し，結果の 値にも何等かの影響を与える：

モンテカルロシミュレーションは の下に多くの検定統計量を生成する：

のもとでの推定される検定統計量の分布：

値の経験的推定はモンテカルロによる推定と一致する：

SignificanceLevel  (2)

デフォルトで，有意水準は0.05になっている：

有意水準を0.001にする：

有意水準は"ShortTestConclusion"にも使われる：

アプリケーション  (12)

データ集合が正規分布から導かれたものかどうかを分析する：

一連の適合度検定を行う：

QuantilePlotの経験的累積分布関数と理論的累積分布関数を視覚的に比較する：

経験的累積分布関数と検定分布のそれとを視覚的に比較する：

バッファロー市の降雪量が正規分布に従うかどうかを調べる：

Jarque–Bera ALM検定とShapiro–Wilk検定を使って正規性を算定する：

SmoothHistogramは検定結果と一致する：

QuantilePlotは比較的よいフィットを示している：

適合度検定を使ってヒストグラムのような可視化が示すフィットを確かめる：

Kolmogorov–Smirnov検定はヒストグラムが示す適合フィットと一致する：

最も明るい100個の星の絶対的な大きさが正規分布に従うかどうか調べる：

自動検定の統計値とp値：

結果を視覚的にチェックする：

多変量データがボックス内で一様分布に従うかどうかを調べる：

境界までの距離(Distance-to-Boundary)検定を使う：

Szekelyのエネルギー検定を使って2つの多変量データ集合を比較する：

偽物と本物の紙幣の測定値の分布は大きく異なる：

周辺分布を視覚的に比較して不一致の起源を調べる：

データが単位円上で一様分布に従っているかどうかを調べる：

Kuiperの検定とWatsonの 検定は円の上での均一性の検定に役立つ：

最初のデータ集合はランダムに分布しており，2番目のデータ集合はクラスタ化している：

モデルがS&P 500指標の日々の点の変化に適しているかどうか調べる：

ヒストグラムは裾部の重い対称分布を示す：

LaplaceDistributionを試す：

非常に大きいデータ集合では，検定分布からの小さい偏差も容易に検出される：

LinearModelFitからの残差を正規性について調べる：

Shapiro–Wilk検定は残差が正規分布に従っていないことを示している：

QuantilePlotでは分布の左裾部に大きい偏差が現れる：

検定統計量の分布のシミュレーションを行いモンテカルロの 値を得る：

SmoothHistogramを使って検定統計量の分布を可視化する：

Anderson–Darling検定からモンテカルロの 値を得る：

DistributionFitTestによって返された 値と比較する：

仮説検定の検出力を推定する：

およその検出力曲線を可視化する：

もとになる分布がStudentTDistribution[2]，検定規模が0.05，サンプルサイズが35の場合のShapiro–Wilk検定の検出力を推定する：

カーネル密度推定を使ったデータ集合の平滑化で，データのもとになっている分布の構造を保存しつつ，ノイズを除去することができる．以下で同じ分布からの2つのデータ集合を作る：

平滑化されていないデータはもとになった分布のノイズの多い推定を与える：

ノイズによってタイプIのエラーが生まれる：

平滑化によってノイズが少なくなり，5%レベルで正しい結論が導かれる：

特性と関係  (16)

デフォルトで，一変量データはNormalDistributionと比較される：

分布母数はデータから推定される：

デフォルトで，多変量データはMultinormalDistributionと比較される：

分布母数が指定されていない場合，それはデータから推定される：

検定分布で母数が指定されていない場合には最尤度推定が使われる：

値は誤判定（タイプIのエラー）の期待される割合を示す：

検定サイズを0.05にすると，結果として約5%の が誤って棄却される：

タイプIIのエラーは，誤りであるにもかかわらず が棄却されない場合に起る：

検定サイズを高めるとタイプIIのエラーの率が低くなる：

有効な検定の 値は のもとでUniformDistribution[{0,1}]である：

Kolmogorov–Smirnov検定を使って一様性を調べる：

各検定の検出力は が誤りであるときにこれを棄却する確率である：

これらの条件下では，ピアソン(Pearson)の 検定の検出力が最も低い：

各検定の検出力はサンプルサイズが小さくなるに従って減少する：

検定の中にはサンプルサイズが小さくても他の検定よりよい結果を出すものもある：

場所による差の検出に向いている検定とそうではない検定がある：

検定の検出力：

尺度の差の検出に向いている検定とそうではない検定がある：

検定の検出力：

ピアソンの 検定の検出力を高めるためには大きいサンプルサイズが必要である：

検定の検出力：

正規性の検定に向いている検定とそうではない検定がある：

Jarque–Bera ALM検定とShapiro–Wilk検定はサンプルが小さい場合の検出力が最も大きい：

正規性の複合仮説のための検定は指定された母数を無視する：

調べる分布の特性によって異なる検定を使う．ある特定の検定に基づいた結果が，常に他の検定に基づいた結果と一致するとは限らない：

緑色の領域は両方の検定による正しい結果である．両方の検定でタイプIIのエラーが認められた場合には，赤色の領域に点が置かれている．灰色の領域は検定結果が一致しない部分である：

検定に先立つ母数の推定は検定統計量の分布に影響する：

のもとでの検定統計量と結果の 値の分布：

推定を考慮に入れないと 値を過大評価してしまう：

分布のフィット検定は，入力がTimeSeriesのときにのみ値に使うことができる：

考えられる問題  (5)

検定によっては予め母数が指定されていなければならず，有効な について推定されてはならないものもある：

通常はモンテカルロ法を使って有効な 値に至ることができる：

分布の多くでは，母数が推定された場合に訂正が適用される：

Jarque–Bera ALM検定は有効な 値のためにはサンプルサイズが最低でも10でなければならない：

モンテカルロ法を使って有効な 値を得る：

Kolmogorov–Smirnov検定とKuiper検定はデータ間のタイを予想しない：

Jarque–Bera ALM検定とShapiro–Wilk検定は正規性の検定にのみ有効である：

離散分布の検定を行う場合は注意深く解釈する必要がある：

ピアソン 検定は離散分布に直接適用できる：

おもしろい例題  (1)

ある検定統計量の分布：

Wolfram Research (2010), DistributionFitTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/DistributionFitTest.html （2015年に更新）.

テキスト

Wolfram Research (2010), DistributionFitTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/DistributionFitTest.html （2015年に更新）.

CMS

Wolfram Language. 2010. "DistributionFitTest." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/DistributionFitTest.html.

APA

Wolfram Language. (2010). DistributionFitTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DistributionFitTest.html

BibTeX

@misc{reference.wolfram_2024_distributionfittest, author="Wolfram Research", title="{DistributionFitTest}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DistributionFitTest.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_distributionfittest, organization={Wolfram Research}, title={DistributionFitTest}, year={2015}, url={https://reference.wolfram.com/language/ref/DistributionFitTest.html}, note=[Accessed: 14-November-2024 ]}