DistributionFitTest

DistributionFitTest[data]

检验 data 是否为正态分布.

DistributionFitTest[data,dist]

检验 data 是否服从分布 dist.

DistributionFitTest[data,dist,"property"]

返回 "property" 的值.

更多信息和选项

  • DistributionFitTest 进行拟合优度假设检验，其中零假设 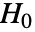假定 data 是从一个服从分布 dist 的总体中抽取的，而备择假设 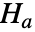认为并非如此.
  • 默认情况下，返回一个概率值或者 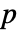值.
  • 一个较小的 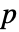值表明 data 不可能来自 dist.
  • dist 可以是任何带有数值型或者符号型参数的符号式分布，也可以是一个数据集.
  • data 可以是单变量 {x1,x2,…} 或者多变量 {{x1,y1,…},{x2,y2,…},…}.
  • DistributionFitTest[data,dist,Automatic] 将选择对于一般备择假设而言，适用于 data 和 dist 的最有效的检验.
  • DistributionFitTest[data,dist,All] 将选择适用于 data 和 dist 的所有检验.
  • DistributionFitTest[data,dist,"test"] 根据 "test" 的结果报告 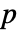值.
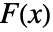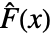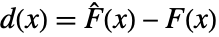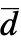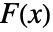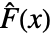  • 许多检验使用的是所检验分布 dist 的累积分布函数 ，数据的经验累积分布函数 ，以及两者的差值 和 =Expectation[d(x),…]. 累积分布函数 和 在零假设 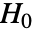下应该是相同的.
  • 下列检验可以用于单变量以及多变量分布：
  • "AndersonDarling"分布，数据基于 Expectation[]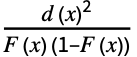
    "CramerVonMises"分布，数据基于 Expectation[d(x)2]
    "JarqueBeraALM"正态性基于偏度和峰度
    "KolmogorovSmirnov"分布，数据基于 sup_x TemplateBox[{{d, (, x, )}}, Abs]
    "Kuiper"分布，数据基于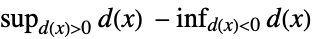
    "PearsonChiSquare"分布，数据基于期望直方图和观测到的直方图
    "ShapiroWilk"正态性基于分位数
    "WatsonUSquare"分布，数据基于 Expectation[]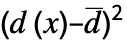
  • 下列检验可用于多变量分布：
  • "BaringhausHenze"正态性基于经验特征函数
    "DistanceToBoundary"均匀性基于到均匀边界的距离
    "MardiaCombined"正态性组合的 Mardia 偏度和峰度
    "MardiaKurtosis"正态性基于多变量峰度
    "MardiaSkewness"正态性基于多变量偏度
    "SzekelyEnergy"数据基于牛顿势能
  • DistributionFitTest[data,dist,"property"] 可以直接给出 "property" 的值.
  • 与检验结果报告相关的属性包括：
  • "AllTests"所有适用的检验列表
    "AutomaticTest"使用 Automatic 时所选择的检验
    "DegreesOfFreedom"检验中所用的自由度
    "PValue" 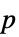值的列表
    "PValueTable" 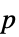值的格式化表格
    "ShortTestConclusion"检验结果的简短描述
    "TestConclusion"检验结论的描述
    "TestData"检验统计量和 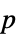值的成对列表
    "TestDataTable" 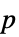值和检验统计量的格式化表格
    "TestStatistic"检验统计量的列表
    "TestStatisticTable"检验统计量的格式化表格
    "HypothesisTestData"返回一个 HypothesisTestData 对象
  • DistributionFitTest[data,dist,"HypothesisTestData"] 返回一个 HypothesisTestData 对象 htd，该对象可用于提取其它检验结果，并利用形式 htd["property"] 获得各属性.
  • 与数据分布相关的属性有：
  • "FittedDistribution"数据的拟合分布
    "FittedDistributionParameters"数据的分布参数
  • 可以给出下列选项：
  • Method Automatic计算 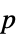值所用的方法
    SignificanceLevel 0.05诊断与报告的临界值
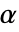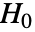  • 对于拟合优度检验，选择一个临界值 使得 仅当 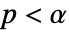时被拒绝. 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的 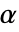值由 SignificanceLevel 选项控制. 默认情况下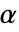， 设为 0.05.
  • 在设置 Method->"MonteCarlo" 下，使用拟合分布在 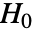的条件下，生成与输入 si 长度相同的 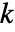个数据集合. 然后，使用来自 DistributionFitTest[si,dist,{"TestStatistic",test}] 的 EmpiricalDistribution 估计 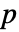值.

范例

打开所有单元关闭所有单元

基本范例  (3)

检验一些数据的正态性：

创建一个 HypothesisTestData 对象，以进一步提取属性：

完整的检验表格：

比较数据的直方图与所检验分布的概率密度函数：

检验一组数据对某特定分布的拟合效果：

提取 Anderson–Darling 检验表格：

用 ProbabilityPlot 验证检验结果：

检验将数据拟合为多元分布的拟合优度：

绘制检验分布的边缘概率分布函数相对于数据的图形，以验证检验结果：

范围  (22)

检验  (16)

检验一些数据的正态性：

对于正态分布的数据，其 值一般较大：

对于非正态分布的数据，其 值一般较小：

设定 Automatic 的第三个参数，以应用一般意义上较有效且适当的检验：

属性 "AutomaticTest" 可用于确定检验的类型：

检验数据是否符合某一种特定分布：

这里没有足够的证据来拒绝这是 WeibullDistribution[1,2] 的良好拟合：

对一个导出分布，检验拟合优度：

比起非混合分布的数据，混合数据的 值较大：

检查数量数据的拟合优度：

检查正态性：

检查特定分布的拟合优度：

检验一个基于公式的分布的拟合优度：

将从数据中估计未指定的参数：

值依赖于所估计的参数：

检验某些数据的多元正态性：

对于正态分布的数据，其 值一般比非正态数据的大：

检验某些数据对于某一特定多变量分布的拟合优度：

分别检验 MultinormalDistribution 和多元 UniformDistribution：

比较两个数据集的分布：

样本大小不一定相等：

比较两种多变量数据集的分布：

与非均匀分布的数据的 值相比，均匀分布的数据 值较大：

进行特定的拟合优度检验：

可同时进行任何检验：

同时进行适用于数据和分布的各种检验：

使用 "AllTests" 来识别所用的检验类型：

创建一个 HypothesisTestData 对象以重复提取属性：

可以提取的属性：

从一个 HypothesisTestData 对象中提取一些属性：

Cramér–von Mises 检验的 值和检验统计量：

同时提取任意多个属性：

Anderson–Darling 的 值和检验统计量的结果：

数据属性  (2)

在参数未指定时获取拟合分布：

提取拟合分布的参数：

绘制拟合分布相对于数据的概率密度函数：

通过拟合优度检验验证拟合：

当参数已经指定好时，返回检验的分布：

作图比较数据与拟合的分布：

报告  (4)

将一组检验结果在表格中显示：

所有适当检验结果的完整表格：

选择一些检验结果列在表格中：

从检验表格中提取相应的项，生成自定义的报告：

值高于 0.05，因此在该水平上没有足够的证据来拒绝分布的正态性：

将一个检验或一组检验的 值列成表：

表格中的 值：

所有适当检验的 值表：

一部分检验的 值表：

汇报一个或一组检验的检验统计量：

表格中的检验统计量：

所有适当检验的检验统计量的表格：

选项  (6)

Method  (4)

使用基于蒙特卡罗的方法，或自动选择最快的方法：

设置样本个数以使用基于蒙特卡罗的方法：

蒙特卡罗估计值随样本数的增大而收敛于真实的 值：

设置随机种子，用在基于蒙特卡罗的方法中：

种子影响生成器的状态，并对生成的 值产生某些影响：

蒙特卡罗模拟生成 条件下的许多检验统计量：

在 条件下该检验统计量的估计分布：

值的经验估计与蒙特卡罗估计一致：

SignificanceLevel  (2)

默认情况下，使用的显著水平为 0.05：

将显著水平设置为 0.001：

显著水平也用于 "ShortTestConclusion"：

应用  (12)

分析一个数据集是否取自一个正态分布：

进行一系列拟合优度检验：

在 QuantilePlot 中作图比较实验和理论累积分布函数：

作图比较经验累积分布函数与检验分布：

判断布法罗市的降雪累积量是否为正态分布：

使用 Jarque–Bera ALM 检验与 Shapiro–Wilk 检验来评定正态性：

SmoothHistogram 与检验结果相符：

QuantilePlot 表明拟合效果相当好：

使用优度检验来验证拟合，其中拟合由图形表示，例如直方图：

柯尔莫哥洛夫–斯米尔诺夫检验的结果与直方图一致，均表明拟合效果良好：

检验前 100 个最亮恒星的绝对星等呈正态分布：

Shapiro–Wilk 检验适用于检验正态性：

作图检查结果：

检验一组多元数据在一个框形区域是否为均匀分布：

使用 Distance-to-Boundary 检验：

利用 Szekely 能量检验比较两个多元数据集合：

伪作和真迹笔记的数据的分布显著不同：

作图比较边缘分布，以确定导致差异的起因：

检验数据在一个单位圆上是否呈均匀分布：

Kuiper 检验与 Watson 检验可以有效检验数据在圆上的均匀性：

第一个数据集为随机分布，第二个聚集成簇：

确定一个模型是否适用于标普 500 强数据的差异度量：

直方图表明这是一个重尾对称分布：

尝试用 LaplaceDistribution：

对于大型数据集合，很容易检测到距检验分布小的偏差：

检验 LinearModelFit 的残差的正态性：

Shapiro–Wilk 检验表明残差非正态分布：

从 QuantilePlot 中可以看出在分布的左尾部有较大的偏差：

模拟一个检验统计量的分布，以获得蒙特卡罗 值：

利用 SmoothHistogram 可视化检验统计量的分布：

获得 Anderson–Darling 检验的蒙特卡罗 值：

与 DistributionFitTest 返回的 值比较：

得到一个假设检验的效能的估计：

可视化近似的效能曲线：

估计 Shapiro–Wilk 检验的效能，其中底层分布为 StudentTDistribution[2]，检验的尺寸为 0.05，且样本大小为 35：

利用核密度估计对一个数据集进行平滑处理可以在保留数据的底层分布结构的同时，删除噪音. 下面的两个数据集是从同一个分布中创建的：

未经平滑处理的数据提供了底层分布的一个带有噪声的估计：

噪声可能导致第一类误差的产生：

平滑处理可以降低噪声，并且在 5% 显著性水平上得到一个正确的结论：

属性和关系  (16)

默认情况下，单变量数据与 NormalDistribution 比较：

分布的参数根据数据估计：

默认情况下，多变量数据与 MultinormalDistribution 比较：

分布中未指定的参数根据数据估计：

对于检验分布的未指定参数，采用最大似然估计：

值表明误确认（第一类错误）的期望比例：

设置检验的大小为 0.05 将导致有5%的概率会错误否定 ：

第二类错误出现在当 非真但却没有被否定时：

提高检验的大小可以降低第二类错误的机率：

有效检验的 值在 下为 UniformDistribution[{0,1}]：

利用柯尔莫哥洛夫–斯米尔诺夫检验验证均匀性：

各检验的效能等于在 不成立时否定它的概率：

在这些条件下，皮尔森 检验的效能最低：

样本越小，各检验的效能越低：

在小样本情况下，一些检验的效能优于其它检验的效能：

在检测位置的不同时，一些检验的效能优于其它检验：

检验的效能：

在检测尺度不同时，一些检验的效能优于其它检验：

检验的效能：

皮尔森 检验需要大型样本以得到高效能：

检验的效能：

在检验正态性时，一些检验的效能优于其它检验：

Jarque–Bera ALM 与 Shapiro–Wilk 检验对于小样本是最有效的：

为正态性的复合假设设计的检验忽略指定的参数：

检验方法不同，所检测的分布性质也不同. 基于某一个检验的结论并不总与其它检验所得到的结论一致：

绿色区域表示两种检验均得到正确结论. 当两种检验均产生第二类误差时，点落到红色区域. 灰色区域表示两种检验的结论不一致.

估计检验前的参数影响检验统计量的分布：

在 下，检验统计量的分布与所得的 值：

不考虑估计方法将对 值估计过高：

分布拟合检验仅当输入为 TimeSeries 时适用于值：

可能存在的问题  (5)

有些检验要求预先指定参数，并不对有效 值进行估计：

通常使用蒙特卡罗方法以达到一个有效的 值：

对于许多分布，在估计参数时要进行修正：

Jarque–Bera ALM 检验要求样本数至少为 10 以得到有效 值：

使用蒙特卡罗方法得到一个有效的 值：

柯尔莫哥洛夫–斯米尔诺夫检验与 Kuiper 检验认为数据中不能存在任何关联：

Jarque–Bera ALM 检验与 Shapiro–Wilk 检验仅对正态性的检验有效：

当某些检验用于离散分布时，需要仔细的解释：

皮尔森 检验直接应用于离散分布：

巧妙范例  (1)

一些检验统计量的分布：

Wolfram Research (2010)，DistributionFitTest，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DistributionFitTest.html （更新于 2015 年）.

文本

Wolfram Research (2010)，DistributionFitTest，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DistributionFitTest.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "DistributionFitTest." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/DistributionFitTest.html.

APA

Wolfram 语言. (2010). DistributionFitTest. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DistributionFitTest.html 年

BibTeX

@misc{reference.wolfram_2024_distributionfittest, author="Wolfram Research", title="{DistributionFitTest}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DistributionFitTest.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_distributionfittest, organization={Wolfram Research}, title={DistributionFitTest}, year={2015}, url={https://reference.wolfram.com/language/ref/DistributionFitTest.html}, note=[Accessed: 14-November-2024 ]}