FourierSinTransform

FourierSinTransform[expr,t,ω]

expr の記号フーリエ正弦変換を与える．

FourierSinTransform[expr,{t1,t2,…},{ω1,ω2,…}]

expr の多次元正弦フーリエ変換を与える．

詳細とオプション

  • フーリエ(Fourier)正弦変換は，フーリエ変換を複素数や負の周波数を必要とせずに見る特別の方法である．
  • ジョセフ・フーリエ(Joseph Fourier)は，彼の有名な変換を，これとフーリエ余弦変換を使って設計した．これらの変換は，信号処理，統計，画像および動画の圧縮等に現在も使われている．
  • 時間領域関数 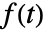のフーリエ正弦変換は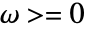，については周波数領域関数 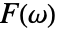である．
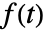  • 関数 のフーリエ正弦変換はデフォルトでは 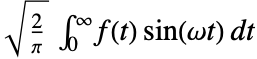で定義される．
  • 関数 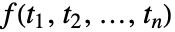の多次元フーリエ正弦変換は，デフォルトで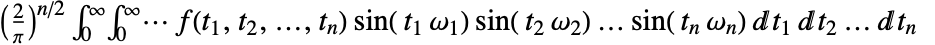，，ベクトル表記を使っているときは(2/pi)^(n/2)int_(t in TemplateBox[{}, PositiveReals]^n )f(t) sin(omega t)dt と定義される．
  • 別の定義はオプションFourierParametersを使用して指定できる．
  • 積分は，第3引数の 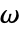が数値で与えられた場合は数値メソッドを使って計算される．
  • 漸近逆フーリエ正弦変換はAsymptoticを使って計算できる．
  • 次は，関連するいくつかのフーリエ変換である．
  • FourierTransform無限連続時間関数(FT)
    FourierSequenceTransform無限離散時間関数(DTFT)
    FourierCoefficient有限連続時間関数(FS)
    Fourier有限離散時間関数(DFT)
  • フーリエ正弦変換は，導関数が急速に減少する関数のSchwartzベクトル空間では自己同形であり，その双対において自己同形に誘導される．これには，絶対可積分関数，多項式の増加の性質の好ましい関数，コンパクトにサポートされた分布が含まれる．
  • したがって，FourierSinTransformはで絶対可積分関数に使えるだけでなく，効果的に変換できる関数または一般化された関数のプールを拡大するために，DiracDeltaのようなさまざまな緩増加分布にも使うことができる．
  • 次は，使用可能なオプションである．
  • AccuracyGoal Automatic目標確度の桁数
    Assumptions $Assumptionsパラメータについての仮定
    FourierParameters {0,1}フーリエ正弦変換を定義するパラメータ
    GenerateConditions Falseパラメータについての条件を含む答を生成するかどうか
    PerformanceGoal$PerformanceGoal最適化するパフォーマンスの局面
    PrecisionGoal Automatic目標精度の桁数
    WorkingPrecision Automatic内部計算精度
  • 次は，FourierParametersのよく使われる設定である．
  • {0,1}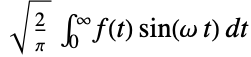
    {1,1}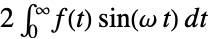
    {-1,1}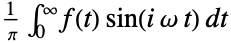
    {0,2Pi}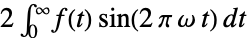
    {a,b}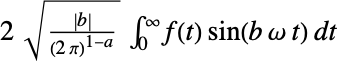

例題

すべて開くすべて閉じる

例  (6)

関数のフーリエ正弦変換を計算する：

関数とそのフーリエ正弦変換をプロットする：

指数関数のフーリエ正弦変換：

異なる規約に関しては，パラメータを変更する：

平方根の逆数のフーリエ正弦変換：

多変量関数のフーリエ正弦変換を計算する：

関数とその変換をプロットする：

単一の点における変換を計算する：

スコープ  (37)

基本的な用法  (3)

記号パラメータ についての関数のフーリエ正弦変換：

変換をプロットする：

三角関数を含むフーリエ正弦変換：

変換をプロットする：

変換をプロットする：

パラメータ の数値についてのフーリエ正弦変換を評価する：

代数関数  (3)

ベキ乗関数のフーリエ正弦変換：

有理関数のフーリエ正弦変換：

についての変換をプロットする：

についての変換をプロットする：

のときの変換：

変換をプロットする：:

についての変換をプロットする：

2つの多項式の商のフーリエ正弦変換：

変換をプロットする：

指数関数と対数関数  (3)

指数関数のフーリエ正弦変換：

についての変換をプロットする：

についての変換をプロットする：

変換をプロットする：

ガウシアンのフーリエ正弦変換：

のときの変換：

変換をプロットする：

についての変換をプロットする：

対数関数のフーリエ正弦変換：

変換をプロットする：

についての変換をプロットする：

についての変換をプロットする：

変換をプロットする：

三角関数  (3)

初等関数の構成：

についての変換をプロットする：

についての変換をプロットする：

についての変換をプロットする：

についての変換をプロットする：

指数関数と三角関数の積のフーリエ正弦変換：

，についての変換をプロットする：

，についての変換をプロットする：

逆正接関数のフーリエ正弦変換：

変換をプロットする：

変換をプロットする：

特殊関数  (8)

Sinc関数を含む式のフーリエ正弦変換：

変換をプロットする：

変換をプロットする：

ExpIntegralEiのフーリエ正弦変換：

変換をプロットする：

Erfの変換：

変換をプロットする：

Erfcの変換：

についての変換のプロット：

SinIntegralを含む式：

変換をプロットする：

CosIntegral：

についての変換のプロット：

BesselJ関数の正弦変換：

についての変換をプロットする：

および についての変換をプロットする：

および についての変換のプロット：

BesselY関数の正弦変換：

についての変換のプロット：

および についての変換のプロット：

区分関数と分布  (4)

区分関数のフーリエ正弦変換：

正弦関数を半周期に制限する：

三角関数：

FresnelSについての変換：

変換をプロットする：

変換をプロットする：

周期関数  (2)

正弦のフーリエ正弦変換：

SquareWaveのフーリエ正弦変換：

一般化された関数  (4)

HeavisideThetaを含む式のフーリエ正弦変換：

DiracDeltaを含むフーリエ正弦変換：

変換をプロットする：

変換をプロットする：

HeavisideLambdaを含むフーリエ正弦変換：

HeavisidePiを含むフーリエ正弦変換：

多変量関数  (2)

二変数指数関数のフーリエ正弦変換：

両方をプロットする：

両方をプロットする：

指数関数とSquareWaveの積のフーリエ正弦変換：

形式的な特性  (3)

一次導関数のフーリエ正弦変換：

二次導関数のフーリエ正弦変換：

フーリエ正弦変換は方程式に縫い込まれる：

数値評価  (2)

単一の点におけるフーリエ正弦変換を計算する：

フーリエ正弦変換を記号的に計算することもできる：

次に の特定の値について評価する：

オプション  (8)

AccuracyGoal  (1)

オプションAccuracyGoalは確度の桁数を設定する：

デフォルト設定では以下のようになる：

Assumptions  (1)

BesselJのフーリエ正弦変換は区分関数である：

FourierParameters  (3)

さまざまなパラメータを持った単位ボックス関数のフーリエ制限変換：

変換の異なる定義にデフォルト以外の設定を使う：

逆変換を得るためには同じFourierParameters設定を使う：

セッションごとにパラメータについて自分の特定の大域選択を設定する：

デフォルトに戻す：

GenerateConditions  (1)

GenerateConditions->Trueを使って結果が有効となる場合に必要なパラメータ条件を得る：

PrecisionGoal  (1)

オプションPrecisionGoalは，積分における相対的な許容範囲を設定する：

デフォルト設定の場合：

WorkingPrecision  (1)

WorkingPrecisionが指定されている場合，計算はその作業精度で行われる：

デフォルト設定の場合：

アプリケーション  (4)

常微分方程式  (1)

初期条件 の以下の常微分方程式について考える：

この常微分方程式にフーリエ正弦変換を適用する：

この変換について解く：

および として逆フーリエ正弦変換を求める：

DSolveValueと比較する：

偏微分方程式  (1)

，について無限拡散問題を解く．のときの初期条件 でである．境界条件は のとき である：

についてのフーリエ正弦変換：

およびとしてこの常微分方程式を解く：

逆正弦変換を計算する：

DSolveValueと比較する：

および のときの特殊ケースについて考える：

積分評価  (2)

次の定積分を について計算する：

指数関数のフーリエ正弦変換を計算する：

フーリエ正弦変換の公式を適用する：

定積分を解く：

Integrateと比較する：

次の定積分を について計算する：

指数関数のフーリエ正弦変換を計算する：

Parsevalの恒等式を適用する：

同様に，以下のようにすることもできる：

定積分を解く：

Integrateと比較する：

特性と関係  (4)

デフォルトで，のフーリエ正弦変換は以下のようになる：

とき，定積分は以下のようになる：

FourierSinTransformと比較する：

Asymptoticを使って漸近近似を計算する：

FourierSinTransformとInverseFourierSinTransformは互いに逆関数である：

FourierSinTransformとFourierTransformの結果は，奇関数については という因数の分だけ異なる：

結果は ω>0については の分だけ異なる：

考えられる問題  (1)

逆フーリエ正弦変換の結果はもととは同じ形式ではないかもしれない：

フーリエ正弦変換はDiracDelta等の一般化された関数によって与えられることがある：

おもしろい例題  (2)

MeijerGによって表現されたフーリエ正弦変換：

基本的なフーリエ正弦変換の表を作成する：

Wolfram Research (1999), FourierSinTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierSinTransform.html （2025年に更新）.

テキスト

Wolfram Research (1999), FourierSinTransform, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierSinTransform.html （2025年に更新）.

CMS

Wolfram Language. 1999. "FourierSinTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/FourierSinTransform.html.

APA

Wolfram Language. (1999). FourierSinTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierSinTransform.html

BibTeX

@misc{reference.wolfram_2025_fouriersintransform, author="Wolfram Research", title="{FourierSinTransform}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FourierSinTransform.html}", note=[Accessed: 28-January-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_fouriersintransform, organization={Wolfram Research}, title={FourierSinTransform}, year={2025}, url={https://reference.wolfram.com/language/ref/FourierSinTransform.html}, note=[Accessed: 28-January-2025 ]}