LaplaceTransform

LaplaceTransform[f[t],t,s]

给出 f[t] 在变量 t 中的符号拉普拉斯变换并返回在变量 s 中的变换 F[s].

LaplaceTransform[f[t],t,]

给出在数值 出的数字拉普拉斯变换.

LaplaceTransform[f[t1,…,tn],{t1,…,tn},{s1,…,sn}]

给出 f[t1,…,tn] 的多维拉普拉斯变换.

更多信息和选项

  • 拉普拉斯变换通常用于将微分和偏微分方程转换为代数方程式，求解并逆变换返回解.
  • 拉普拉斯变换还广泛应用于控制论和信号处理中，作为一个以传递函数和转移矩阵为形式来表示和控制线性系统的方法. 拉普拉斯变换和逆变换也是一种在时域和频域之间变换的方法.
  • 函数 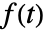的拉普拉斯变换定义为 .
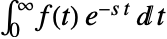  • 多维拉普拉斯变换由 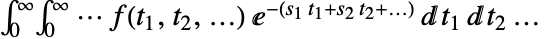给出.
  • 如果赋给第三个参数 s 的是数值，则使用数值法计算积分.
  • 可使用 Asymptotic 计算渐进拉普拉斯变换.
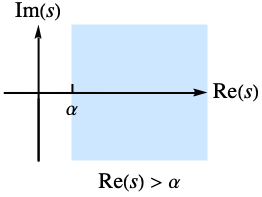
  • 只对于半平面 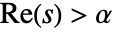内的复数值 s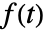， 的拉普拉斯变换才存在.
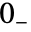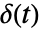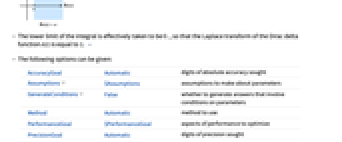
  • 积分的下极限实际上为 ，使得 Dirac delta 函数 的拉普拉斯变换等于 1. »
  • 可给出以下选项：
  • AccuracyGoalAutomatic追求的绝对准确度
    Assumptions $Assumptions对参数的设定
    GenerateConditions False是否给出涉及参数条件的答案
    MethodAutomatic所用的方法
    PerformanceGoal$PerformanceGoal优化的目标
    PrecisionGoalAutomatic追求的精度
    PrincipalValueFalse是否求出柯西主值
    WorkingPrecisionAutomatic内部计算使用的精度
  • 用 GenerateConditions"ConvergenceRegion" 获取拉普拉斯变换的收敛域.
  • 在 TraditionalForm 中，LaplaceTransform 用 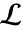输出. »

范例

打开所有单元关闭所有单元

基本范例  (4)

计算函数的拉普拉斯变换：

定义一个分段函数：

计算它的拉普拉斯变换：

在一个点上计算拉普拉斯变换：

计算多变量函数的拉普拉斯变换：

定义一个多变量分段函数：

计算它的拉普拉斯变换：

范围  (67)

基本用法  (4)

计算符号参数 t 的函数的拉普拉斯变换：

三角函数的拉普拉斯变换：

参数 s 取一个数值，计算拉普拉斯变换：

TraditionalForm 格式：

初等函数  (13)

幂函数的拉普拉斯变换：

平方根函数：

多项式的拉普拉斯变换：

指数函数：

指数函数与线性函数的积：

含有三角函数的表达式：

含有双曲函数的表达式：

指数函数与线性函数的比：

正弦函数与线性函数的比：

初等函数的复合函数：

对数函数：

对数函数与幂函数的积：

对数函数的平方：

特殊函数  (10)

误差函数与平方根函数组成的复合函数的拉普拉斯变换：

贝塞尔函数：

含有贝塞尔函数的积：

正弦积分函数：

Laguerre 多项式：

Airy 函数：

切比雪夫多项式：

Struve 函数：

Fresnel 函数：

Gamma 函数：

超几何函数：

分段函数  (9)

分段函数的拉普拉斯变换：

将正弦函数限制到半周期：

指数函数，将左侧去掉：

三角形函数：

多项式函数，将左侧去掉：

斜坡函数：

UnitStep：

UnitStep 与余弦函数的积：

Floor 的拉普拉斯变换：

周期函数  (5)

SquareWave 的拉普拉斯变换：

TriangleWave：

SawtoothWave：

周期为 的全波整流函数：

整流波：

广义函数  (5)

HeavisideTheta 的拉普拉斯变换：

DiracDelta:

DiracDelta 的导数：

HeavisideLambda：

HeavisidePi：

多变量函数  (9)

常数的二元拉普拉斯变换：

指数函数：

幂函数：

BesselJ：

平方根：

余弦函数与平方根函数的复合函数：

多变量幂函数的拉普拉斯变换：

余弦函数：

对数：

形式属性  (6)

拉普拉斯变换是线性运算符：

的拉普拉斯变换是 的拉普拉斯变换在 处的值：

一阶导数的拉普拉斯变换：

二阶导数的拉普拉斯变换：

函数与单项式乘积的拉普拉斯变换：

拉普拉斯变换同时作用于方程的两侧：

数值运算  (3)

在一个点上计算拉普拉斯变换：

或者，先符号式计算拉普拉斯变换：

然后针对 的具体值进行计算：

绘制用数值法获得的拉普拉斯变换：

对于某些函数，不能符号式计算拉普拉斯变换：

用数值法计算拉普拉斯变换并绘制：

计算平面中一个点的多变量拉普拉斯变换：

分数阶微积分  (3)

MittagLefflerE 函数的拉普拉斯变换：

-域的 ComplexPlot：

到时域的拉普拉斯逆变换：

涉及参数的 MittagLefflerE 函数的拉普拉斯变换：

到时域的拉普拉斯逆变换：

CaputoD 分数阶导数的拉普拉斯变换：

应用于正弦函数：

与正弦函数的 CaputoD 导数的 LaplaceTransform 相比较：

选项  (4)

Assumptions  (1)

用 Assumptions 指定参数范围：

GenerateConditions  (1)

当结果有效时，用 GenerateConditions->True 获得参数条件：

Principal Value  (1)

由于在 处有奇点，以下函数的拉普拉斯变换没有定义：

用 PrincipalValue 获取积分的柯西主值：

Working Precision  (1)

用 WorkingPrecision 获取任意精度的结果：

应用  (12)

常微分方程  (5)

用拉普拉斯变换求解一个微分方程：

求拉普拉斯变换：

求逆变换：

绘制解：

用 DSolve 直接求解：

求解下面的微分方程：

求拉普拉斯变换：

求逆变换：

绘制解：

求解 RL 电路，求电流 ：

用 DSolveValue 验证：

RL 电路的格林函数：

用格林函数求解 RL 电路：

求解常微分方程组：

分数阶微分方程  (3)

用拉普拉斯变换解分数阶微分方程：

求拉普拉斯变换：

求逆变换：

绘制解：

直接用 DSolve 求解：

求解以下分数阶积分-微分方程：

求拉普拉斯变换：

求逆变换：

直接用 DSolve 求解：

以下等式描述了 1.9 阶的分数谐波振荡器：T

求拉普拉斯变换：

求逆变换：

绘制解：

直接用 DSolve 求解：

计算积分  (2)

计算下面的积分：

计算拉普拉斯变换，并交换拉普拉斯变换和积分的顺序：

在 上积分：

用 InverseLaplaceTransform 获取原来的积分：

验证结果：

涉及贝塞尔函数的积分：

更改变量 ，引入辅助变量 ：

应用拉普拉斯变换，并交换拉普拉斯变换和积分的顺序：A

在 上积分：

用 InverseLaplaceTransform 获取 ：

原来的积分等于 ：

验证结果：

其他应用  (2)

用级数展开式计算拉普拉斯变换：

奇数系数消失：

可用 Regularization 求变换过的级数的和：

直接用 LaplaceTransform 验证结果：

用级数展开式计算 Sinc 的拉普拉斯变换：

奇数系数消失：

验证结果：

属性和关系  (3)

用 Asymptotic 计算渐近近似：

LaplaceTransform 和 InverseLaplaceTransform 是互逆的：

对数值近似值用 NIntegrate：

NIntegrate 计算拉普拉斯参数 s 的数值的转换：

可能存在的问题  (1)

化简需要返回原形式：

巧妙范例  (2)

LaplaceTransform 按 MeijerG 执行：

创建基本的拉普拉斯变换表：

Wolfram Research (1999)，LaplaceTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LaplaceTransform.html （更新于 2023 年）.

文本

Wolfram Research (1999)，LaplaceTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LaplaceTransform.html （更新于 2023 年）.

CMS

Wolfram 语言. 1999. "LaplaceTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/LaplaceTransform.html.

APA

Wolfram 语言. (1999). LaplaceTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LaplaceTransform.html 年

BibTeX

@misc{reference.wolfram_2024_laplacetransform, author="Wolfram Research", title="{LaplaceTransform}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/LaplaceTransform.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_laplacetransform, organization={Wolfram Research}, title={LaplaceTransform}, year={2023}, url={https://reference.wolfram.com/language/ref/LaplaceTransform.html}, note=[Accessed: 15-November-2024 ]}