MultinomialDistribution
MultinomialDistribution[n,{p1,p2,…,pm}]
n 回試行,確率 piの多項分布を表す.
詳細
- 多項分布における非負の整数
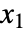 ,
, 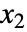 , …,
, …, 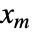 のベクトル
のベクトル 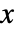 の確率は
の確率は 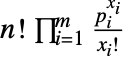 である.
である. - 試行回数 n は任意の正の整数でよく,
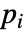 は
は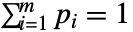 となる任意の非負の実数でよい.
となる任意の非負の実数でよい. - MultinomialDistributionでは,n と piは無次元量でよい. »
- MultinomialDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- MultinomialDistribution[n,{p1,p2,…,pm}]は,
 および
および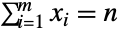 を満足し,
を満足し,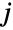 番目の各(一変量)周辺分布が
番目の各(一変量)周辺分布が 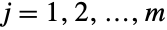 についてBinomialDistributionを持つことで特徴付けられる整数のすべてのタプル
についてBinomialDistributionを持つことで特徴付けられる整数のすべてのタプル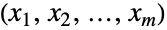 からなる
からなる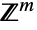 の部分集合上でサポートされる離散多変量統計分布を表す.言い変えるなら,各変数
の部分集合上でサポートされる離散多変量統計分布を表す.言い変えるなら,各変数 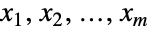 は
は 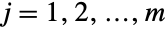 について xjBinomialDistribution[n,pj]を満足する.多項分布は正の整数 n および
について xjBinomialDistribution[n,pj]を満足する.多項分布は正の整数 n および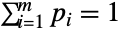 を満足する非負の実数のベクトル{p1,p2,…,pm}でパラメータ化され,両者がともに分布の陪平均,分散,共分散を定義する.
を満足する非負の実数のベクトル{p1,p2,…,pm}でパラメータ化され,両者がともに分布の陪平均,分散,共分散を定義する. - 多項分布は,タイプ i で母集団の piパーセントを表す集団からの置換を伴う,n 回抽選が行われるような場合をモデル化する.これは,n 個のボールが取り出され,代りに異なる m タイプのボールが入っている壺から置換される壺モデルとして可視化することができる.
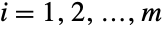 について,タイプ i のボールの割合は百分率で piであるという制約条件がある.多項分布は1708年にフランス人数学者のPierre Raymond de Montmortの随筆によってはじめて解析された(これは,最初期に研究された多変量多項分布の一つである).この分布は,以来,素粒子物理学における気体分子運動論,会計学における過大申告等を含むさまざまな現象の研究ツールとなっている.また,分割表,電気通信のモデリング,医学的疫学,光子計数等の解析に広く使われている.
について,タイプ i のボールの割合は百分率で piであるという制約条件がある.多項分布は1708年にフランス人数学者のPierre Raymond de Montmortの随筆によってはじめて解析された(これは,最初期に研究された多変量多項分布の一つである).この分布は,以来,素粒子物理学における気体分子運動論,会計学における過大申告等を含むさまざまな現象の研究ツールとなっている.また,分割表,電気通信のモデリング,医学的疫学,光子計数等の解析に広く使われている. - RandomVariateを使って,多項分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,MultinomialDistribution[n,{p1,p2,…,pm}]] (より簡略な表記では xMultinomialDistribution[n,{p1,p2,…,pm}])を使って,確率変数 x が多項分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[MultinomialDistribution[n,{p1,p2,…,pm}]]およびCDF[MultinomialDistribution[n,{p1,p2,…,pm}]]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Covariance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が多項分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック多項分布を推定することが,FindDistributionParametersを使ってデータを多項分布にフィットすることができる.ProbabilityPlotを使って記号多項分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号多項分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された多項分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って多項分布を含む高次元分布を構築することが,ProductDistributionを使って多項分布を含む独立成分分布の結合分布を計算することができる.
- MultinomialDistributionは,他の数多くの分布と関係がある.MultinomialDistributionは,上で説明したように,BinomialDistributionと関係がある.MultinomialDistributionの一次元周辺分布のPDFはそれぞれBinomialDistributionを持つが,多変量周辺分布は名前付きの分布には簡約されない.MultinomialDistributionの壺モデルとMultivariateHypergeometricDistributionの壺モデルは,後者の分布モデルが置換なしに「引く」という意味で関係している.多項分布は,一変量BinomialDistributionとの関係によって,BernoulliDistribution,NormalDistribution,PoissonDistribution,BetaBinomialDistribution,NegativeBinomialDistributionとも関連している.
例題
すべて開くすべて閉じるスコープ (8)
一変量周辺分布はBinomialDistributionに従う:
無次元のQuantityを使ってMultinomialDistributionを定義する:
アプリケーション (5)
候補者が2名でそのうちの1名が単純多数決で当選となる選挙があるとする.![]() 人の投票者のそれぞれが確率
人の投票者のそれぞれが確率 ![]() で候補1に,確率
で候補1に,確率 ![]() で候補2に投票する.ただし
で候補2に投票する.ただし ![]() で,投票者は棄権することもできる.
で,投票者は棄権することもできる.![]() で
で ![]() である場合に,浮動票の確率は次のようになる:
である場合に,浮動票の確率は次のようになる:
3個の容器に5個のボールを分け入れる.各容器を同じ確率で選ぶものとして,空の容器ができない確率を求める:
SurvivalFunctionを使って同じ確率を計算する:
![]() 個の容器に
個の容器に ![]() 個のボールを同じ確率で分配する.
個のボールを同じ確率で分配する.![]() と
と ![]() の値が違っても空の容器が出ない確率を求める:
の値が違っても空の容器が出ない確率を求める:
カスタマーサービスセンターに電話をすると,0.4の確率で相手が通話中,0.1の確率で目的とは違う相手に繋がり,目的の相手に繋がる場合を含め3つの場合がある.6回電話して4回は通話中で繋がらず,目的の相手に2回繋がる確率を求める:
6回電話して少なくとも2回目的とは違う相手に繋がる確率を求める:
911通報の30%が救急車の要請,15%が消防署への通報,残りが警察への通報である都市がある.次の10回の救急通報のうち2回が救急車の要請,1回が消防署への通報,7回が警察への通報である確率を求める:
特性と関係 (3)
考えられる問題 (2)
テキスト
Wolfram Research (2010), MultinomialDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/MultinomialDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "MultinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MultinomialDistribution.html.
APA
Wolfram Language. (2010). MultinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultinomialDistribution.html
