PascalDistribution
PascalDistribution[n,p]
母数が n と p のパスカル(Pascal)分布を表す.
詳細

- パスカル分布は二項待ち時間分布とも呼ばれる.
- パスカル分布における整数値
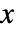 の確率は,
の確率は,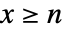 では
では![TemplateBox[{{x, -, 1}, {n, -, 1}}, Binomial] p^n(1-p)^(x-n) TemplateBox[{{x, -, 1}, {n, -, 1}}, Binomial] p^n(1-p)^(x-n)](Files/PascalDistribution.ja/3.png) であり,その他の場合はゼロである.
であり,その他の場合はゼロである. - PascalDistribution[n,p]は非零の成功確率 p で n 回成功するまでの試行回数の分布を与える.
- PascalDistributionでは,n は正の整数でよく,p は1以下の正の実数でよい.
- PascalDistributionでは,n と p は無次元量でよい. »
- PascalDistributionは,Mean,CDF,RandomVariate等の関数とともに用いることができる.
予備知識
- PascalDistribution[n,p]は,整数値
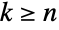 について定義され,試行の成功数と成功確率をそれぞれ表す整数母数 n (
について定義され,試行の成功数と成功確率をそれぞれ表す整数母数 n ( )と実数母数 p (
)と実数母数 p ( ) によって決定された離散統計分布を表す.パスカル分布は離散的で単峰性の確率密度関数(PDF)を持つ.パスカル分布は,「負の二項分布」としてまとめられる数多くの分布の一つであるが,負の二項分布(NegativeBinomialDistribution)と混同してはならない.
) によって決定された離散統計分布を表す.パスカル分布は離散的で単峰性の確率密度関数(PDF)を持つ.パスカル分布は,「負の二項分布」としてまとめられる数多くの分布の一つであるが,負の二項分布(NegativeBinomialDistribution)と混同してはならない. - パスカル分布は確率分布の中で最も早く研究されたものの一つであり,ブレーズ パスカル(Blaise Pascal)の1670年代の研究まで遡ることができる.パスカル分布は,負の二項分布族の一員として見ると,各取り出しが互いに独立で成功確率が p のときに,ある特定の色のビー玉を n 個壺から取り出すためのビー玉の取り出し回数を説明する壺モデルとして実現することができる.この分布は,誕生以来,NegativeBinomialDistribution[n,p]の整数 n の場合として実現されており,負の二項分布族に含まれているために,数多く応用されている(例:事故統計および無線通信).この分布のその他の応用例には,人口統計のモデル化,心理学データ,品質管理,待ち行列理論等がある.
- RandomVariateを使って,パスカル分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,PascalDistribution[n,p]](より簡略な表記では xPascalDistribution[n,p])を使って,確率変数 x がパスカル分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[PascalDistribution[n,p],x]およびCDF[PascalDistribution[n,p],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合がパスカル分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックパスカル分布を推定することが,FindDistributionParametersを使ってデータをパスカル分布にフィットすることができる.ProbabilityPlotを使って記号パスカル分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号パスカル分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたパスカル分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってパスカル分布を含む高次元分布を構築することが,ProductDistributionを使ってパスカル分布を含む独立成分分布の結合分布を計算することができる.
- PascalDistributionは,他の数多くの統計分布と関連している.上述の通り,パルカル分布は負の二項分布族の一員であり,したがって,(非整数 n についてのポリヤ分布としても知られる)NegativeBinomialDistributionと定性的に関係している.GeometricDistributionはPascalDistributionの変換分布(TransformedDistribution)である.ここで,変量 u-1の累積分布関数は,uPascalDistribution[1,p]であるときは常に,GeometricDistribution[p]のそれと厳密に等しい.PascalDistributionはNegativeBinomialDistributionの変換でもある.PascalDistribution[n,p]の確率密度関数は,n→∞のときに,μ と σ についてNormalDistribution[μ,σ]の確率密度関数に収束するのに対し,平均(Mean)と標準偏差(StandardDeviation)はPascalDistribution[n,p]のそれにそれぞれ収束する.PascalDistributionはPoissonDistribution,PoissonConsulDistribution,BinomialDistribution,NegativeBinomialDistribution,MultinomialDistribution,NegativeMultinomialDistributionとも関係がある.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
大きい n の極限の値は標準的なNormalDistributionの尖度である:
無次元のQuantityを使ってPascalDistributionを定義する:
アプリケーション (7)
PascalDistributionのCDFは右連続関数の例である:
表が3回出るまでのコイントスの回数のシミュレーションを行う:
10回目のコイントスで7回目の表が出た.コインが公正な場合にそのような事象が起こる確率を求める:
コインが不正であるかもしれないと仮定して,p が最も取りそうな値を求める:
バスケットボールの選手が4回成功するまでフリースローを続ける.この選手がフリースローで得点する確率は0.7である.このフリースローのシミュレーションを行う:
ファウルする確率が独立で1分間につき0.1だと仮定して,30分間のファウルのシミュレーションを行う:
バスケットボール選手は6回ファウルすると退場になる.ファウルで退場になるまでの期待されるプレー時間を求める:
4つのデータパクレットを含むデータストリームがデータ順序に関する情報なしで繰り返し送信されている.全パクレットが正しい順序であるデータストリームが2回目に届くまでの送信回数の分布を求める:
送信回数が20回以下でパクレットが正しい順序で2回目に受信される確率を求める:
2回目に正しい順序でデータストリームが届くまでの平均試行回数を求める:
パケットの順序が正しいデータストリームが2回目に届くまでの回数のシミュレーションを行う:
2つのチャンネルを通してメッセージが送信.成功率は等しい.各チャンネルが少なくとも3つのメッセージを受信までに必要な送信回数が,5回を超えない確率を求める:
特性と関係 (5)
PascalDistribution[n,p]は ![]() のとき正規分布に収束する:
のとき正規分布に収束する:

GeometricDistributionはパスカル分布を変換したものである:
NegativeBinomialDistributionとパスカル分布の違いはシフトである:
テキスト
Wolfram Research (2010), PascalDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/PascalDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "PascalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PascalDistribution.html.
APA
Wolfram Language. (2010). PascalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PascalDistribution.html