リスト

リストの作成リスト要素の追加，削除，変更
オブジェクトの集合を作るリストの結合
数値の表を作るリストの集合論的扱い
リスト要素の操作リストの並べ替え
ベクトルと行列リストの分割
部分リストの構成リストにおける順序
リスト要素の判定と検索多次元リストの並べ替え
リストの作成
計算を進めていく上で，複数のオブジェクトを1つにまとめて扱えると便利になる．複数のオブジェクトをまとめたものをリストと呼ぶ．後で説明するが，リストはWolfram言語の一般的な構造であり非常に重要なものである．
リストの簡単な例として，{3,5,1}がある．これは3つの数から構成されるリストである．リストにすることで3つのオブジェクトを一括で扱えるようになる．つまり，すべての要素について同じ計算をしたり，まとめて一変数としても扱えるようになる．
3つの数の要素からなるリストを作る：
各要素を二乗した後，それぞれに 1 を加える：
2つのリストで対応する要素同士の差を取る．リストの長さ（要素の個数）は同じでなければならない：
% は，リストの全要素を引用する：
リストは1つの引数として扱われる．「数学関数」の数学関数はどれでも同様に使える：
変数に数値を割り当てられるように，変数にリストを割り当てることもできる．
リストを v に割り当てる：
v は，現れるたびにリストに置き換えられる：
オブジェクトの集合を作る
「リストの作成」において，複数の数をまとめて扱うための一方法としてのリストの使い方に触れた．このチュートリアルでは，リストの違った使い方をいろいろ見ていく．Wolfram言語の数あるオブジェクトの中でも最も適用範囲が広く，かつ，機能的に強力なオブジェクトはリストであることが理解できると思う．そして，Wolfram言語のリストが，数学やコンピュータサイエンスにおけるいくつかの基本的な考え方を一般化したものであることも見えてくるだろう．
リストの基本的な機能は，種類によらず複数の式をまとめるための1つの方法を提供することである．
これは数値のリストである：
数式のリストを生成する：
リストを微分することもできる：
x に3を代入した値を求めることもできる：
Wolfram言語に組み込まれているほとんどの数学関数は，リストの各要素に別々に作用することができるように設定されている．ただし，このことは関数によっては当てはまらないときがある．ユーザ定義の関数 f は，それに対して特別な設定がなされない限り，リスト全体にしか作用しない．ユーザ定義の関数をリストの各要素にも適用可能にするには，「リストや式への関数の部分的適用」と「構造操作」で説明するMapとThreadを使う必要がある．
数値の表を作る
数値の表としてリストを使うことができる．表は，パラメータに値を設定した数列の値について式を繰返し評価することで作成することができる．
が1から6までの，の値の表を作る：
今度は， がからまでの，の値の表を作る：
Nをリストに作用させ，数値を確認する：
数式を要素とした表を作成することも可能である：
Tableで使う反復子の記述は，「和と積」で説明した和Sumと積Productのものと同じ整数表記である：
0.25刻みでxを0〜1に変えた表を作成する：
Tableで作ったリストには，別の演算を行うことも可能である：
TableFormを作用させると，表の形式でリストを表示することができる．TableFormのTとFは大文字であることに注意：
これまで見てきた表の作成例は，すべて単一の表を変えて作成した．複数のパラメータに依存した表を作成することもできる，多次元の表を作るときも「和と積」の標準的な反復子の記述法が使われる．
を1から3へ， を1から2へと変えたときの の表を作成する：
上の例における表は，リストのリストである．外側のリストの要素は，iの反復値に対応している．また，内側のリストの要素は， を固定したときの の反復値に対応している．
場合によっては，何も増分しないで，特定の式を何回も繰返し評価するだけで表を生成したい．
記号xを4つ並べたリストを作る：
これは，{1,2,3,4}からサンプルを取った4組の数のペアのリストを与える．Tableは，リストの各要素についてRandomSample[{1,2,3,4},2]の評価を行う．このため，4つの異なるサンプルが得られる：
これは，リスト{1,4,9,16}中のそれぞれの i の値についてを評価する：
これは，3×2の表を作る：
この表では，行の長さは徐々に変化する反復変数i に依存する：
Tableを使って任意次数の配列を生成することができる．
これは，三次の2×2×2配列を生成する．これはリストのリストのリストである：
Table[f,{imax}]
f を imax 回計算し，値をリストとして構成する
Table[f,{i,imax}]
i が1から imax までの間での f の値のリストを構成する
Table[f,{i,imin,imax}]
i が imin から imax までの間での値のリストを構成する
Table[f,{i,imin,imax,di}]
刻み幅 di を使う
Table[f,{i,imin,imax},{j,jmin,jmax},…]
多次元の表を生成する
Table[f,{i,{i1,i2,…}]
i が連続的に値 i1, i2, …を取る f の値のリストを構成する
TableForm[list]
リストを表形式で表示する
表の生成に使う関数
「リスト要素の操作」で説明した操作法でリストから任意の要素を抽出することができる．
これは，表を作成し，sqという名前を与える：
これは，表の第3要素を与える：
これは，3番目から5番目までの要素のリストを与える：
これは2×2の表を作成し，mという名前を与える：
表を構成しているリストのリストから，第1要素のサブリストを抽出する：
次に，第2要素を抽出する：
こうすれば，両方の操作を1回でできる：
mを表の形式で表示する：
t[[i]]
or
Part[t,i]
リスト t の i 番目のサブリストを抽出する（t〚i〛とも入力する）
t[[i;;j]]
or
Part[t,i;;j]
リスト t の i 番目から j 番目までの要素のリストを与える
t[[{i1,i2,…}]]
or
Part[t,{i1,i2,…}]
リスト t の i1番目，i2番目…の要素のリストを与える
t[[i,j,…]]
or
Part[t,i,j,…]
リスト t の t[[i]][[j]]…に対応する部分を与える
表の要素抽出の方法
「リスト要素の操作」で述べたように，Wolfram言語においてリストは配列と同じように扱うことができる．例えば，リストのリストは二次元配列である．それを表形式でレイアウト表示したなら，各要素に割り当てられた2つの添数は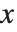， と 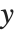の座標のような働きをする．
リスト要素の操作
リスト処理に使う操作法では，リスト全体を単体のものとして扱うことを前提としている場合が多い．しかし，時にはリスト内の個別の要素を抽出したり割り当てたりする必要がある．
リストの要素に「指標」を与えることでその要素を参照することができる．リスト左端の要素が1で，右方向に移るに従い2, 3, ...と高くなるように番号が付けられている．
{a,b,c}
リストの定義（中カッコで要素をくくる）
Part[list,i]
or
list[[i]]
リストの部分抽出（単一要素）．リスト list の i 番目の要素を抽出する（第1要素は list[[1]]）
Part[list,{i,j,…}]
or
list[[{i,j,…}]]
リストの部分抽出（複数要素）．リスト list の i, j, …番目の複数要素からなる新たなリストを構成する
Part[list,i;;j]
list の i 番目から j 番目までの要素のリスト
リストの定義と要素抽出
2番目の要素を抽出する：
既存のリストから別のリストを構成する：
リストを変数vに割り当てる：
vから特定要素を抽出する：
リストを変数として定義すると，他のプログラミング言語で使う「配列」と同じようにリストが扱えるようになる．例えば，v[[i]]に値を割り当てることでリストの要素を再設定することができる．
Part[v,i]
or
v[[i]]
リストの部分抽出．リストから i 番目の要素を抽出する
Part[v,i]=value
or
v[[i]]=value
リストの部分的割当て．i 番目の要素に値を割り当てる
配列的なリストの使い方
リスト変数を定義する：
3番目の成分を0に変更する：
vに割り当てられたリストの変更内容を確認する：
ベクトルと行列
Wolfram言語では，ベクトルと行列もそれぞれ，リストおよびリストのリストで表される．
{a,b,c}
ベクトル
{{a,b},{c,d}}
行列
ベクトルと行列の表記
2×2の行列を作る：
列1を取り出す：
要素 を取り出す：
2要素のベクトルを定義する：
オブジェクトp，qはスカラーとして扱われる：
ベクトルは要素ごとに加算される：
ドット演算子でつないで，内積（スカラー積）を計算する：
行列にベクトルを掛けることもできる：
行列同士でもよい：
ベクトルと行列でもよい：
この掛け算はスカラーになる：
Wolfram言語においてベクトルと行列は，ともに構成上はリストなので，行ベクトルと列ベクトルを区別する必要はない．
Table[f,{i,n}]
i=1,2,…,n で f を計算し，n 次元ベクトルを作成する
Array[a,n]
{a[1],a[2],…}要素からなる n 次元ベクトルを作成する
Range[n]
リスト{1,2,3,…,n}を構成する
Range[n1,n2]
リスト{n1,n1+1,…,n2}を構成する
Range[n1,n2,dn]
リスト{n1,n1+dn,…,n2}を構成する
list[[i]]
or
Part[list,i]
list の i 番目の要素を抽出する
Length[list]
list のリスト長（構成成分の個数）を得る
c v
ベクトルをスカラー倍する
a.b
2つのベクトルの内積
Cross[a,b]
2つのベクトルの外積（a×b としても入力可）
Norm[v]
ベクトルのユークリッドノルム
ベクトルに関連した関数
Table[f,{i,m},{j,n}]
i が1 〜m，j が1〜n の区間で f を計算し，m×n 要素の行列を作る
Array[a,{m,n}]
i,j 要素 a[i,j]で m×n 要素の行列を作る
IdentityMatrix[n]
n×n 要素の単位行列を作る
DiagonalMatrix[list]
list の対角要素から正方行列（対角行列）を作る
list[[i]]
or
Part[list,i]
行列 list の i 番目の行を抽出する
list[[All,j]]
or
Part[list,All,j]
行列 list の j 番目の列を与える
list[[i,j]]
or
Part[list,i,j]
行列 list の i,j 列の要素を抽出する
Dimensions[list]
list で与えられる行列の次元数を調べる
行列に関連した関数
Column[list]
list の要素を列に表示する
MatrixForm[list]
行列形式で list を表示する
ベクトルと行列のフォーマットコンストラクト
要素 の3×3の行列 を作成する：
こうすると，sを通常の二次元行列の形式で表示することができる：
未知数要素からなるベクトルを作る．このベクトルは，ベクトル要素が何であっても有効な一般式の導出に使うことができる：
未知数要素を使い3×2要素の行列を作成する．「関数のリスト化」に，違った種類の要素を作るためにArrayをどのように使うかの説明がある：
作った行列の次元数を調べる：
3×3の対角行列を作成する：
c m
行列のスカラー倍
a.b
2つの行列のドット積
Inverse[m]
逆行列
MatrixPower[m,n]
行列の n 番目のベキ
Det[m]
行列式
Tr[m]
対角和（トレース）
Transpose[m]
転置行列
Eigenvalues[m]
固有値
Eigenvectors[m]
固有ベクトル
行列を使った演算操作のいくつか
これは，前の例で定義した未知数要素からなる2×2の行列である：
行列式を計算する：
これは，mの転置行列である：
mの逆行列をシンボル的な形で求める：
これは，3×3の有理数行列である：
この行列の逆行列を求める：
もとの行列と逆行列の内積を取ると，単位行列が得られる：
3×3の行列を作る：
Eigenvaluesを使うと，行列の固有値を計算することができる：
行列の要素を数値化する：
固有値を数値解析的に近似する：
上記の関数の他に，行列演算のための組込み関数がまだいろいろあるが，それらは，「Wolfram言語における線形代数」で説明する．
部分リストの構成
First[list]
リスト list の1番目の要素を抽出する
Last[list]
リストの最後の要素を抽出する
Part[list,n]
or
list[[n]]
リストの n 番目の要素を抽出する
Part[list,-n]
or
list[[-n]]
リストの後ろから数えて n 番目の要素を抽出する
Part[list,m;;n]
要素 m から n を抽出する
Part[list,{n1,n2,…}]
or
list[[{n1,n2,…}]]
n1, n2, …番目の要素を抽出したリストを作成する
リスト要素の抽出
このリストを以下の例で使用する：
tの最終要素を抽出する：
第3要素を抽出する：
要素3から6までのリストである：
第1，第4要素から新たなリストを作る：
Take[list,n]
リスト list で前から n 個の連番要素を抽出し，リストに構成する
Take[list,-n]
リストで後ろから n 個の連番要素を抽出し，リストに構成する
Take[list,{m,n}]
リストで m 番目から n 番目までの連番要素を抽出し，リストに構成する
Rest[list]
リスト list から先頭要素を除いたリストを作る
Drop[list,n]
リスト list から初めの n 個の要素を除いたリストを作る
Most[list]
リスト list から最終要素を除いたリストを作る
Drop[list,-n]
リスト list から後ろの n 個の要素を除いたリストを作る
Drop[list,{m,n}]
リスト list の m 番目から n 番目の要素を除いたリストを作る
リストからの連番要素の抽出と除去
前に定義したリストtから最初の3要素を取り出す：
同じリストから末尾の3要素を取り出す：
2〜5番目の要素を取り出す：
3番目から7番目まで，ステップ2（1つおき）で取り出す：
tの最初の要素を除いたリストを作る：
tの最初の3つの要素を除いたリストを作る：
tの第3要素だけが除かれる：
「式のリスト的操作」で詳しく説明するが，ここで見てきた部分抽出の関数は，一般化することでリストだけでなく他のどんな式にも適用することができる．
ここで取り上げた関数は，リスト中の位置関係に基づいて要素を取り出すためのものである．「パターンにマッチする式の検索」で説明するが，SelectやCases等の関数を使えば，要素の位置関係ではなく，要素の特徴に基づいた抽出や検索もできるようになっている．
リスト要素の判定と検索
Position[list,form]
リスト list の中で form が現れる位置を探す
Count[list,form]
リストlist の中で form が現れる回数を検索
MemberQ[list,form]
form がリスト list に含まれるかどうかを判定
FreeQ[list,form]
form がリスト list に含まれないかどうかを判定
リスト要素の判定と検索
「部分リストの構成」では位置関係や添数に従いリスト要素をどう抽出するかを説明している．ここでは，要素の持つ値に基づいて要素の検索や判定をどう行うかを説明する．
入力リストにおけるaの要素の位置を列挙したリストを構成する：
Countを使い，aが現れる頻度を調べる：
判定結果から，aは{a,b,c}の要素である：
一方，dは要素ではない：
3×3の単位行列を作りmと呼ぶ：
判定結果によると，mのどこかに0がある：
こうすると，0の位置が列挙される：
「パターンにマッチする式の検索」で説明してあるように，CountとPosition，およびMemberQとFreeQの関数を使うことで，任意のリスト要素を検索することはもちろん，特定の「パターン」に合った要素のクラスを探すこともできる．
リスト要素の追加，削除，変更
Prepend[list,element]
リスト list に要素 element を第1要素として追加する
Append[list,element]
リスト list に要素 element を最終要素として追加する
Insert[list,element,i]
リスト list の前から数えた位置 i に要素 element を挿入する
Insert[list,element,-i]
リスト list の後ろから数えた i 番目の位置に要素 element を挿入する
Riffle[list,element]
リスト list の要素の間に element を挿入する
Delete[list,i]
リスト list の位置 i の要素を削除する
ReplacePart[list,i->new]
list 中の位置 i にある要素を new で置き換える
ReplacePart[list,{i,j}->new]
list[[i,j]]を new で置き換える
リスト要素の追加・削除
リストの先頭にxを追加する：
位置2の要素になるようにxをリストに挿入する：
xをリストの要素の間に挿入する：
リストの3番目の要素をxで置換する：
2×2行列の要素1，2を置換する：
ReplacePartのような関数は明示的なリストを取って新たなリストを与える．しかし，場合によってはリストに「その場で」変更を加え，新たなリストは生成したくない場合もあるだろう．
v={e1,e2,…}
リストに変数を割り当てる
v[[i]]=new
i 番目の要素に新たな値を割り当てる
リスト要素の再設定
vがリストであると定義する：
このようにして3番目の要素をxに設定する：
vが変更された：
m[[i,j]]=new
行列の(i,j) 番目の要素を置換する
m[[i]]=new
i 番目の行を置換する
m[[All,i]]=new
i 番目の列を置換する
行列の部分の再設定
mが行列であると定義する：
このように行列の最初の列を設定する：
こうすると最初の列の全要素が0になる：
リストの結合
Join[list1,list2,…]
リストを連結する
Union[list1,list2,…]
リストを結合し，重複する要素を除去して，順序正しく並べ替えたリストを構成する
Riffle[list1,list2]
list1と list2の交互的要素
リストの結合
Joinを使うと，リストをいくつでもつなぎ合せることができる：
Unionを使うと重複を解消してリストを結合できる：
Riffleは要素を交互にしてリストを結合する：
リストの集合論的扱い
Wolfram言語は，通常，リストの要素を入力されたままの順序で内部保持する．しかし，リストを数学的な集合として扱いたいときは，要素の並び順を無視した方がよいかもしれない．
Union[list1,list2,…]
入力リスト listi を結合し，重複する要素があれば解消して順序正しく並べ替えたリストを構成する
Intersection[list1,list2,…]
すべての入力リスト listi に共通する要素でリストを構成する
Complement[universal,list1,…]
すべての入力リスト listi にない入力リスト universal の要素でリストを構成する
Subsets[list]
list のすべての部分集合を与える
DeleteDuplicates[list]
list から重複する要素をすべて削除する
集合論的な関数
Unionを使うと，入力リストの和集合を作ることができる：
Intersectionで入力リストの共通集合を作る：
Complementを使い，最初の集合から他の集合を引いた補集合を構成する：
リストの部分集合を与える：
DeleteDuplicatesはリストから重複する要素をすべて削除する：
リストの並べ替え
Sort[list]
入力リスト list を標準的順序（小から大の数字，アルファベット順等）に並べ替えたリストを構成
Union[list]
入力リスト list で重複する要素があったらその重複を解消して標準的順序に並べ替えたリストを構成
Reverse[list]
入力リスト list の要素の並ぶ順序を反転させたリストを構成
RotateLeft[list,n]
リスト list の全要素を n 回左方向に位置を入れ替えた（左回転させた）リストを構成
RotateRight[list,n]
リスト list の全要素を n 回右方向に位置を入れ替えた（右回転させた）リストを構成
リストの並べ替え
標準的順序で入力要素を並べ替える．標準的順序とは，アルファベット順や，数字の順序を意味する：
入力要素を標準的順序に並べ替え，要素の重複を解消する：
入力リストの要素を2つ分左方向に移動する：
右方向の回転を命令するには，回転数に負の値を指定するか，RotateRightを使う：
PadLeft[list,len,x]
list の長さが len になるように左側を x で充填する
PadRight[list,len,x]
list の右側を充填する
リストの充填
長さが10になるようにリストをxで充填する：
リストの分割
Partition[list,n]
入力リスト list の全要素を n 個ずつのサブリストに分割したリストを構成する
Partition[list,n,d]
d をオフセットとする部分リストを構成する
Split[list]
入力リスト list を同一要素ごとにまとめて分けたリストを構成する
SplitBy[list,f]
f が適用されたときに，list を同じ値の要素からなるサブリストに分割する
Gather[list]
list の要素を同一要素ごとに集めたサブリストにする
GatherBy[list,f]
list 中の要素を，f を適用したときに同じ値を返す要素ごとのサブリストにする
リストの分割
リストを入力する：
リストの要素を一対のサブリストに再編成する．1つ残った末尾要素は捨てられる：
3個の要素からなるサブリストに再構成する．サブリストの間で重なり合う部分はない：
隣り合うサブリストの要素が1つのオフセットだけ離れた3個の要素からなるサブリストに再構成する：
同一要素ごとにまとめて分けたリストを作成する：
次は整数の乱数リストである：
上記のリストを順番に奇数，偶数のグループに分ける：
整数をサブリストに集める：
整数を，3を法とした同値性に基づいたサブリストに集める：
Tuples[list,n]
list の要素のすべての n 要素集合を作成する
Tuples[{list1,list2,…}]
i 番目の要素が listi からのすべての可能な集合のリストを作成する
リストの要素の可能な要素集合を見付ける
リストから2要素を取る可能なすべての組合せである：
それぞれのリストから要素を1個取る可能なすべての組合せである：
リストにおける順序
Sort[list]
list 中の要素を順に並べる
Ordering[list]
Sort[list] における list 中の要素の位置
Ordering[list,n]
Ordering[list] 中の最初の n 個の要素の位置
Ordering[list,-n]
Ordering[list] 中の最後の n 個の要素の位置
Permutations[list]
list の可能な全順序
Min[list]
list の最小要素
Max[list]
list 中の最大要素
リスト中の順序
これは，数のリストである：
これは，t中の要素を順に与える：
これは，tの要素の位置を最小のものから最大のものへという順で与える：
これはSort[t]に等しい：
リスト中の最小要素が得られる：
多次元リストの並べ替え
行列，表，多次元配列はすべてネストしたリストのことである．Wolfram言語はこれらのリストの処理のための多くの関数を提供している．
Flatten[list]
多次元リスト list のすべてのレベルのネストを外す
Flatten[list,n]
入力リスト list において，レベル1からレベル n までのサブリストのネストを外す
Partition[list,{n1,n2,…}]
入力リスト list をサイズ n1×n2×…のブロックに分割する
Transpose[list]
リストの最上層の2つのレベルを入れ替える
RotateLeft[list,{n1,n2,…}]
後続するレベルを位置 ni 分ずらす
PadLeft[list,{n1,n2,…}]
長さが ni になるように後続するレベルを充填する
多次元リストの操作を行う関数
すべてのレベルにあるサブリストのネストを外す．この操作は内側のカッコをすべて取り払う作業と思えばよい：
今度は1つのレベルのサブリストのネストだけを外す：
上記の他にも，各種の多次元リストの操作が可能である．それらのいくつかに関しては「リストの操作」で触れる．