数

数的类型任意精度的计算
复数任意精度的数
数值量机器精度数
不同形式的数之间的转换区间算术
精确和近似结果不定结果和无穷结果
数值精度控制数值运算
数的类型
Wolfram 系统中建立了四种基本的数的类型.
Integer
任意长度的精确整数
Rational
integer/integer 的最简形式
Real
近似实数，具有任意指定的精度
Complex
具有 number+number I 形式的复数
Wolfram 系统中数的基本类型.
有理数是两个整数的比，化简为最简形式：
近似实数通过小数点来区分：
近似实数可以有任意的位数：
复数中可以有整数或有理数的成分：
复数中也可以有近似实数的成分：
123
精确整数
123.
近似实数
123.0000000000000
具有确定精度的近似实数
123.+0.I
包含近似实数成分的复数
数 123 的几种类型.
通过查看数的头可以区分在 Wolfram 系统中数的不同类型.（虽然 Wolfram 系统中的数像其他表达式一样有头，但没有明确的元素来提取他们.）
对象 123 被看作精确整数，具有头 Integer：
小数点的出现使 123. 在 Wolfram 系统中被处理为近似实数，具有头 Real：
NumberQ[x]
检验 x 是否是数
IntegerQ[x]
检验 x 是否是整数
EvenQ[x]
检验 x 是否是偶数
OddQ[x]
检验 x 是否是奇数
PrimeQ[x]
检验 x 是否是素数
Head[x]===type
检验数的类型
检验不同类型的数.
NumberQ[x] 检测任何类型的数：
5. 作为实数处理 Real，所以 IntegerQ 得出 False：
如果经常使用复数，应该注意一些微妙之处. 当输入一个数如 123. 时，Wolfram 系统把其作为近似实数处理，而假定其虚部是精确的0. 有时可能会输入虚部是具有一定精度的0，但不是精确的0的近似复数.
当虚部是精确整数 0 时，Wolfram 系统把该复数简化为实数：
虚部只是具有确定精度的0，故 Wolfram 系统保持其为复数形式：
区分虚部是精确的0的复数和虚部是具有一定精度的0的复数，似乎太学究气了. 但是，例如，当我们在"多值函数" 中讨论复数的幂和根的解释时，这个区别就很有意义了.
在 Wolfram 系统中确定数的类型的一种方法是使用 Head[expr] 来找出头. 然而，在许多情况下，最好使用函数如IntegerQ，其明确地检测特定的类型. 当这些函数的参数是所需类型时，该函数设置返回 True，否则，返回 False. 因此，除非 x 是一个整数，否则，IntegerQ[x] 将返回 False.
复数
在 Wolfram 语言中，你可以通过包括常量 I，等于 ，输入复数. 确保你所输入的是大写的 I.
如果使用笔记本，也可以键入 EsciiEsc 来以 输入 I （见"笔记本中的数学表示法"）. 在输出中使用的是形式 . 请注意，平常的 i 指的是名为 的变量，而不是 .
给出复数 ：
复数的除法：
复指数的值：
x+I y
复数
Re[z]
复数的实部
Im[z]
复数的虚部
Conjugate[z]
共轭复数 或
Abs[z]
复数的模
Arg[z]
在 中的幅角
复数运算.
数值量
NumberQ[expr]
检验 expr 是否为一个数
NumericQ[expr]
检验 expr 是否有一个数值
检验数值量.
Pi 是一个符号，所以Pi+3 并不明确是一个数：
但是是一个数值值：
求出 Pi+3 明确的数值值：
Wolfram 语言知道常数例如 Pi 是数值量. 还知道标准的数学函数例如 Log 和 Sin 当其参数是数值时有数值值.
Log[2+x] 包含 x，因此不是数值量：
许多函数明确使用数值量值：
一般，Wolfram 语言假定任何具有属性 NumericFunction 的函数当其参数是数时，将产生数值值. 在 Wolfram 语言中所有标准的数学函数已经具有该属性. 当用户定义自己的函数时，可以明确设置属性来告诉 Wolfram 语言假定当这些函数的参数是数时，他们有数值值.
不同形式的数之间的转换
IntegerDigits[n]
整数 n 在十进制中的每一位数的列表
IntegerDigits[n,b]
整数 n 在 b 进制中的每一位数的列表
IntegerDigits[n,b,len]
在每位数的列表中的左端补0，使列表长度达到 len
IntegerLength[n]
整数 n 在十进制中的位数数目
IntegerLength[n,b]
整数 n 在 b 进制中的位数数目
IntegerExponent[n,b]
整数 n 在 b 进制中末尾零的个数
RealDigits[x]
近似实数 x 在十进制中每一位数的列表，并给出小数点左边位数的数目
RealDigits[x,b]
实数 x 在 b 进制中的每一位数的列表
RealDigits[x,b,len]
实数 x 在 b 进制中的前 len 位的每一位数的列表
RealDigits[x,b,len,n]
从 bn 的系数开始的前 len 位的列表
FromDigits[list]
从其十进制每位数的序列重构该数
FromDigits[list,b]
从其 b 进制每位数的序列重构该数
FromDigits["string"]
从字串构建该整数
FromDigits["string",b]
从 b 进制中的字串构建该整数
IntegerString[n]
整数 n 在十进制下每位数构成的字串
IntegerString[n,b]
整数 n 在 b 进制下每位数构成的字串
在数和数位列表或字串之间的转换.
一个整数在十六进制下每位数的列表：
给出每位数的列表，并且给出小数点左边位的数目：
56的二进制位序列，左边添加0使长度达到8：
从其二进制序列重构原来的数：
56 是二进制字串：
再重构原来的数：
b^^nnnn
b 进制下的数
BaseForm[x,b]
以 x 在 b 进制下的形式打印
IntegerString[n,b]
代表整数 n 在 b 进制下的一个字串
其他进制下的数.
在超过10的进制中，9以上的数字用字母 a–z 表示.
二进制的数 在十进制下是 ：
把37以二进制形式显示出来：
把37的二进制表示以一个字串的形式显示：
一个十六进制的数：
可以用十六进制的数进行运算. 这里结果以十进制形式给出：
以十六进制的形式给出实数和整数：
可以用其他进制给出近似实数和整数：
这是八进制 的前几位：
以下给出前 15 个八进制位的显式列表：
从 系数开始给出了 15 个八进制数：
"数字的输出格式" 将介绍如何打印各种形式下的数. 如果用户想要建立自己的格式，那么常常需要使用MantissaExponent 来分离实数的各个部分.
MantissaExponent[x]
给出包含 x 的尾数和指数的列表
MantissaExponent[x,b]
给出 b 进制下的尾数和指数
分离数的尾数和指数.
给出数的尾数和指数分离的列表：
精确和近似结果
标准电子计算器按照特定的精度（譬如说10个十进制数位）进行所有的计算. 然而用 Wolfram 语言，常能获得精确结果.
对 Wolfram 语言给出精确结果，即使有31个十进制数：
用户可以告诉 Wolfram 语言给出近似的数值结果，如同计算器那样，只要在末尾输入 //N. N 代表“数值”. 必须是大写字母. "表达式输入的特殊方式" 将解释 // 的含义.
给出近似的数值结果：
Wolfram 语言能以有理数的形式给出结果：
//N 总是给出近似的数值结果：
expr//N
给出 expr 的近似值
获得数的近似值.
当键入整数时，例如 7，Wolfram 语言假定其是精确的. 如果键入带明确小数点的数，例如 4.5，Wolfram 语言假定其仅精确到固定的十进制小数位.
一个精确有理数，被化简到最少项：
当给出带小数点的数时，Wolfram 语言产生近似数值结果：
只要有小数点出现，Wolfram 语言就给出近似数值结果：
当算术表达式中任一个数带有明确小数点，将得到整个表达式的近似数值结果：
数值精度
正如"精确和近似结果"讨论的那样，Wolfram 语言能处理任意位数的近似实数. 一般地，近似实数的精度（precision）是其在十进制下的，在计算中作为有效数字处理的位数. 近似实数的准确度（accuracy）是其在十进制下小数点后边的位数. 请注意，为了在数字处理上达到完全的一致，精度和准确度经常具有与数位的整数数目不相对应的值.
Precision[x]
x 的十进制下的有效数位的总数
Accuracy[x]
x 的十进制下小数点后边的有效数位的数目
实数的精度和准确度.
产生一个具有30位精度的数：
给出该实数的精度：
准确度相对较低，因为这里小数点后边只有部分位数：
该数具有小数点右边的所有位数：
准确度大于精度：
一个近似实数总是在其值上具有一定的不确定性，这与我们所知之外的数位相关. 我们可以把精度看做是提供了这种不确定性的相对大小的一种测量. 而准确度给出了不确定性绝对大小的测量.
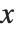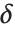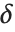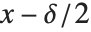Wolfram 语言的设置可以使如果一个数 具有不确定性 ，那么其真实值可以位于大小为 从 到 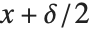的区间的任意位置. 我们定义一个具有准确度 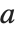的近似数的不确定性为 ，而一个具有精度 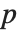的非零近似数的不确定性为 .
Precision[x]
Accuracy[x]
关于不确定性的精度和准确度定义.
加上或减去小于不确定性的一定数量没有明显可见的效果：
N[expr,n]
使用任意精度数近似计算 expr 到 n 位精度
N[expr]
仅使用机器精度数据近似计算 expr
使用任意精度和机器精度的数值计算.
Wolfram 语言区分两种近似实数： 任意精度数和机器精度数. 任意精度数能包含任何位数，并且保持其精度. 另一方面，机器精度数总是保护相同数目的位数，并且不保持其精度信息.
近似等于 的机器精度数：
这两个都是任意精度数：
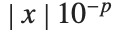下面的详细讨论表明，机器精度数值直接利用用户的计算机系统的数值能力，因此使用他们可以使计算进行得很快. 但是机器精度数的灵活性比任意精度数差的多，并且可能需要困难度高的数值分析来确定获得的结果是否是正确的.
MachinePrecision
用来表明机器精度数的精度规格
$MachinePrecision
用户的计算机系统的机器精度
MachineNumberQ[x]
检验 x 是否是一个机器精度数
机器精度数.
返回标记 MachinePrecision 来表明这是一个机器精度数：
在这台电脑中，机器精度数具有略少于16位的十进制位数：
当输入一个近似实数时，Wolfram 语言必须决定以机器精度还是任意精度处理. 除非用户指明，否则，如果输入的数少于Ceiling[$MachinePrecision+1] 位时，Wolfram 语言将以机器精度处理该数，否则如果用户输入更多的位数时，将以任意精度处理该数.
123.4
机器精度数
123.45678901234567890
某些计算机系统上的任意精度数
123.45678901234567890`
所有计算机系统上的任意精度数
123.456`200
具有200位精度的任意精度数
123.456``200
具有200位准确度的任意精度数
1.234*^6
科学表示法下的机器精度数（1.234×106）
1.234`200*^6
具有200位精度在科学表示法下的数
2^^101.111`200
具有200个二进制位精度的二进制数
2^^101.111`200*^6
科学表示法下的二进制数（101.1112×26）
数的输入形式.
当 Wolfram 语言打印数的时候，通常以尽可能容易阅读的形式给出. 但如果用户想取出由 Wolfram 语言显示出的数，然后在后面作为 Wolfram 语言的输入使用，则需要保证没有信息丢失.
在标准输出形式下，Wolfram 语言显示一个数到6位，如下所示：
在输入形式下，Wolfram 语言显示出所知道的所有位：
一个标准输出形式下的任意精度数：
在输入形式中，Wolfram 语言明确指明数的精度，并给出额外的数位以确保该数能正确地进行重构：
令 Wolfram 语言不明确指明精度：
InputForm[expr,NumberMarks->True]
在所有的近似数中使用记号 `
InputForm[expr,NumberMarks->Automatic]
只在任意精度数中使用记号 `
InputForm[expr,NumberMarks->False]
不使用记号 `
控制数的显示形式.
NumberMarks 选项的缺省设置在 InputForm 中和诸如 ToString 和 OpenWrite 的函数中由 $NumberMarks 给出. 因此通过重新设置 $NumberMarks，能改变整个 InputForm 中被显示的形式.
若缺省地使 Wolfram 语言在输入形式中包含数记号：
甚至一个机器精度数现在也带有明显的数记号：
即使不带数记号，InputForm 仍在科学表示法中使用 *^：
在进行数值计算中，有时不可避免地会出现所得结果低于用户想要的精度. 特别，当得到的数值结果非常接近0时，用户可能很想假定结果是真正的零. 函数 Chop 允许用户用精确的整数0代替接近0的近似实数.
Chop[expr]
用0代替 expr 中的所有小于10-10 的近似实数
Chop[expr,dx]
用0代替小于 dx 的数
清除接近0的数.
这个运算给出很小的虚部：
使用 Chop 可以略去虚部：
任意精度的计算
使用 //N 获得近似结果时，Wolfram 语言就像标准的计算器一样：给出固定位数的有效数字的结果. 而且 Wolfram 语言还可以给出用户指定位数的有效数字的计算结果. 这使用户能在 Wolfram 语言中得到任意精度的结果.
expr//N or N[expr]
expr 的近似数值
N[expr,n]
使用 n 位精度计算 expr 的数值
数值计算函数.
给出 的固定位数的有效数字的近似值. Pi//N 与 N[Pi] 作用相同：
给出 的40位近似值：
的30位近似值：
做任何数值计算都会产生截断误差. 当用户增加数值精度，误差将相应地变小. 确定在增加精度时，结果不再变化，常常是检验结果是否正确的好办法.
的结果很像一个整数. 为了检验其实际上不是整数，需要使用足够高的精度：
任意精度的数
当对任意精度的数进行计算时，Wolfram 语言在各处都保持对精度的跟踪. 一般，Wolfram 语言将尽力给出可能的最高精度，给出用户的输入具有的精度.
Wolfram 语言把任意精度数处理为量的值，这个量的某些位是已知的，某些位是未知的. 一般，任意精度数 x 的由Precision[x] 给出的位数是已知的，后面的无穷位是完全不知道的.
计算 ，尽力得到10位精度：
在某一点之后，所有数位都未定：
当用户进行计算的时候，Wolfram 语言记录在用户的结果中任何可能受到输入中未知数位影响的数位. 其设置了结果的精度，以使任何被影响的数位不被包括在内. 这个过程确保由 Wolfram 语言返回的数字是正确的，无论未知数位的取值如何.
计算 ，尽力得到30位精度：
在上述情况下，结果有准确的30位精度：
如果输入只有很小的精度，那么 Wolfram 语言不能给出那样高精度的输出：
如果想要 Wolfram 语言假定参数精确的 142/1000，那么必须明确表示：
在许多计算中所得结果的精度因“舍入误差”而降低. 一个典型的情况是两个很接近的数进行相减，所得结果依赖于每个数的高阶位. 并且结果的精度比原来数的精度低的多.
两个输入数都有20位的精度，但结果的精度低的多：
在一个数中添加一些位而另一个数中不添加，这样不能使添加的位在结果中表现出来：
函数输出的精度以一个复杂的方式依赖于输入的精度. 变化得快的函数，其输出精度较低，这是因为与输入中的不确定性有关的输出变化是更大的. 而接近于常数的函数给出的输出其精度比输入的更高.
变化很快的函数，其输出的精度比其输入的精度低：
计算到20位精度的 ：
所得结果与整数 1 相加，给出更高的精度：
值得注意，以不同方式进行同一运算所得结果的精度是不大相同的. 通常，在计算中，一旦损失了精度，是不可能恢复的. 精度的损失就是有关信息的丢失.
接近于1的40位数：
与 1 相加得出另一个40位数：
最初的精度一直被保持：
这种方式计算 1+x 将损失精度：
这种方式得出的结果精度相当低：
以不同方式进行同一运算所得结果的精度不同意味着，其中包括两个近似实数间的比较必须谨慎处理. 在测试两个实数是否“相等”时，Wolfram 语言先求出二者之差，并检测结果是否在给定的精度内“与0一致”.
这两个数在给定的精度内是相等的：
Wolfram 语言用于计算数学函数的内部算法被设计来保持尽可能高的精度. 大多数情况下，Wolfram 语言内部函数给出结果的精度与输入的精度很接近. 但在有些情况下，做不到这一点，Wolfram 语言将给出较低精度的结果. 如果输入的精度较高，Wolfram 语言在内部计算中将使用较高的精度. 并且通常能给出较高精度的结果.
N[expr]
计算 expr ，给出机器精度的结果
N[expr,n]
数值计算 expr ，得到 n 位精度的结果
数值计算.
如果表达式仅包含整数和精确数值量，那么 N[expr,n] 在所有情况下都给出 n 位精度的结果. 应该认识到，要做到这一点，Wolfram 语言有时必须执行更高精度的内部中间运算.
全局变量 $MaxExtraPrecision 指定在中间计算中，允许多少额外的数位.
变量
默认值
$MaxExtraPrecision50
使用的最大额外精度
控制中间计算的精度.
为了得到正确答案，Wolfram 语言自动增加内部运算的精度：
使用默认设置 $MaxExtraPrecision=50，Wolfram 语言不能得到正确答案：
告诉 Wolfram 语言在内部计算中用更多的位：
得到正确答案：
将 $MaxExtraPrecision 重新设置为默认值：
甚至在做给出精确结果的计算时，Wolfram 语言仍然偶尔使用某些内部运算中的近似数，以使 $MaxExtraPrecision 的值能发挥作用.
在近似数的精度内，Wolfram 语言求出结果：
在 $MaxExtraPrecision 的默认值下，Wolfram 语言不能给出此式的结果：
重设 $MaxExtraPrecision，使 Wolfram 语言得出结果：
在进行降低精度的计算中， 我们有可能最终得到不具有任何有效数位的数字. 但即使在这种情况下，Wolfram 语言仍然保持数字的准确度信息. 给出一个不具有有效数位但具有准确度a 的数字，Wolfram 语言仍然可以告诉我们该数的实际值一定位于区间 {-10-a,+10-a}/2 之间. 默认情况下，Wolfram 语言以 0.×10e 的形式显示该这样的数.
一个计算到20位精度的数：
没有留下任何有效数位：
Wolfram 语言仍然保持结果的准确度：
对结果加上精确的 1 将生成具有相当高精度的数：
用数字的精度为特征的一个微妙之处在于任何与零一致的数都必须被视为具有零精度. 这样做的理由是这样一个数没有任何可以被视为有效位的数位，因为其所有已知的数位刚好是零.
给出一个值一致为零的数.     
该数没有可识别的有效精度：
但仍具有一定的准确性，刻画了其不确定性的特点：
如果您的计算结果很可能接近零，可以方便地指定用户想获得的准确度，而不是精度.
N[expr,p]
计算 expr，得到 p 位精度的结果
N[expr,{p,a}]
计算 expr，得到最多 p 位精度和 a 位准确度的结果
N[expr,{Infinity,a}]
计算 expr，得到任意精度和 a 位准确度的结果
指定准确度以及精度.
一个符号表示的表达式：
表明该表达式等于零：
N 不能确保获得精度为20的结果：
但是能获得准确度为20的结果：
当 Wolfram 语言在任意精度的未知位的潜在影响下工作时，其缺省地假定这些位在不同的数中是完全无关的. 但这个假定不可能产生很高的精度，能导致不必要的精度损失.
特别，在一个计算中，如果两个数以同样的方式生成时，其一些未知位可能是相等的. 那么当二者相减时，未知位可以相消. 但是在未知位总是无关的假定下，Wolfram 语言将丢失这样的相消.
一个计算到20位精度的数：
1+d 有34位精度：
这个量具有较低的精度，因为 Wolfram 语言假定每个 d 中的未知位是无关的：
数值计算有时依赖不同数的未知位间的相消而产生较高精度的结果. 如果能确定未知位最终相消，那么用户可以明显地在未知位处引入任意数字，在整个运算中使用这些任意数字，然后将他们消去，并得到更高精度的结果.
SetPrecision[x,n]
产生具有 n 位精度的十进制数，如果有必要的话，使用二进制的零填充
SetAccuracy[x,n]
产生具有 n 位准确度的十进制数
用来修改精度和准确度的函数.
给 d 增加了10个任意的数字：
增加的位数被消去：
结果的精度是44位，而不是34位：
SetPrecision 通过在二进制添加0来增加精度. 有时，Wolfram 语言在任意精度数中存贮的位数多于显示出来的位数，此时，SetPrecision 将在使用完这些额外的位数后再添加零.
设置一个数具有40位精度. 额外的位来自二进制到10进制进行的换算：
变量
默认值
$MaxPrecisionInfinity
使用的最大总精度
$MinPrecision0
使用的最小精度
全局精度控制参数.
给出全局赋值 $MinPrecision=n，用户能在计算的每步有效地使用 SetPrecision[expr,n]. 这意味着既使任意精度数种的正确位数变得低于n，该数将总是被添加到 n 位精度.
如果设置 $MaxPrecision=n 以及 $MinPrecision=n，那么能迫使所有的任意精度数有固定的 n 位精度. 结果，这使 Wolfram 语言像处理机器精度数一样处理任意精度数，但是有更高的精度.
固定精度计算使某些计算效率更高. 但是如果不仔细分析，将不能确定所得结果有多少位是正确的.
具有20位精度的很小的数：
在 Wolfram 语言通常的算法下，此式能被很好的计算：
让 Wolfram 语言使用固定精度算法：
结果的前几位是正确的，但其余的是错误的：
恢复$MinPrecision 和 $MaxPrecision 的默认值：
机器精度数
当一个计算中出现机器精度时，整个计算都是在机器精度下进行的. Wolfram 语言的结果也是机器精度数.
当输入包含机器精度时，Wolfram 语言以机器精度进行整个计算：
Zeta[5.6] 产生机器精度结果，所以 N 是不恰当的：
给出高精度的结果：
当对任意精度数进行计算时，像 "任意精度数" 讨论的那样，Wolfram 语言总是保持对结果精度的跟踪，并且正确地给出由输入给定的精度的数位. 但是，当对机器精度数进行计算时，Wolfram 语言总是给出机器精度的结果，不管结果在输入形式下的所有位是否是正确的.
两个机器精度数相减：
其结果具有机器精度：
这是结果的所有位：
在使用 Wolfram 语言的机器精度数值计算中，用户可能得到错误数位的事实在许多方面令人很不满意. 然而 Wolfram 语言使用固定精度做这些计算的根本原因是计算效率方面的因素.
Wolfram 语言通常被设置为使用户与所用的计算机系统的细节尽可能地隔离开来. 但是，在处理机器精度数种，如果Wolfram 语言不利用特定计算机的一些特有的性质，将丢失太多的精度.
很重要的一点是所有的计算机有特殊的硬件或微代码来进行特定的固定精度的浮点运算. 在进行机器精度的数值运算时，Wolfram 语言利用这些特点.
一个典型的安排是所有的机器精度数在 Wolfram 语言中被表示为所用计算机系统中的“双浮点运算”，在大多数现代计算机中，这种数包含64个二进制位，产生16个十进制位的尾数.
使用计算机的内部浮点能力的主要优点是速度快. 任意精度的数值计算，其并不直接利用这些能力，通常比机器精度运算慢许多倍.
使用内部浮点能力有好些缺点. 前面已提到的一个是迫使所有的数都有固定的精度，与对他们而言什么精度是合理的无关.
第二个缺点是，机器精度的处理随计算机不同会有所变化. 在机器精度数的运算中，Wolfram 语言受特定计算机的浮点算法系统的摆布. 两个计算机的浮点算法不同时，在这两个计算机上的 Wolfram 语言机器精度运算得到的结果会有所不同.
$MachinePrecision
十进制精度位数
$MachineEpsilon
机器精度数的最小正数，1.0加上该数给出的结果与1.0是可区分的
$MaxMachineNumber
机器精度数的最大值
$MinMachineNumber
机器精度中的最小正值
$MaxNumber
任意精度数的最大值
$MinNumber
正的任意精度数的最小值
特定计算机系统上数的性质.
因为在任意特定计算机系统上的机器精度数由一个确切位数的二进制数所代表，而两个很接近的数有同样的位数类型，所以不能被区分. 参数 $MachineEpsilon 给出 1.0 和与其最接近的数间的距离，该距离有一个独特的二进制表达式.
给出所用计算机系统的 $MachineEpsilon 的值：
尽管显示为 1.，Wolfram 语言知道结果大于1：
InputForm 表明结果不是确切的1：
减去1给出 $MachineEpsilon:
再次显示为 1.：
但在这种情况下，咋机器精度下，结果与1. 没有差别：
减1给出0：
机器精度数不仅有受限的精度，也有受限的量值，如果生成的数的幅度大于 $MaxMachineNumber，Wolfram 语言将自动转换该数成任意精度的形式.
所用计算机系统能处理的机器精度数的最大值：
Wolfram 语言自动转换任何大于 $MaxMachineNumber 的结果为任意精度数：
另一个计算，其结果在机器精度数的范围之外：
截至版本 11.3，如果机器精度计算产生的数幅度上小于 $MinMachineNumber，那么 Wolfram 语言会产生一个警告. 然而，结果会保留为次正规机器数，在二进制尾数中有前导零.
这是最小机器精度数，可以放入计算机系统的正则格式：
Wolfram 语言发出关于计算的警告，当产生的数小于 $MinMachineNumber，但是不会自动转换成任意精度算术：
有可能丢失所有有效数字并最终以机器数零作为答案：
使用 SetPrecision 转换成任意精度以避免下溢：
区间算术
Interval[{min,max}]
从 min 到 max 的区间
Interval[{min1,max1},{min2,max2},…]
从 min1 到 max1、从 min2 到 max2, … 等区间的并
实区间的表示法.
代表 到 之间的所有数：
到 之间所有数的平方总在 到 之间：
取倒数给出两个不同的区间：
Abs 把这两个区间折迭到一起：
可以在许多种函数中使用区间：
有些函数自动生成区间：
IntervalUnion[interval1,interval2,…]
求若干区间的并集
IntervalIntersection[interval1,interval2,…]
求若干区间的交集
IntervalMemberQ[interval,x]
检验点 x 是否位于一个区间中
IntervalMemberQ[interval1,interval2]
检验区间 interval2 是否完全位于区间 interval1 中
区间运算.
求两个区间的交集：
可以使用 Max 和 Min 求区间的端点：
检验一列区间的哪些包含点7：
不仅能使用具有精确量的区间，也能使用具有近似数的区间. 即使对机器精度数，Wolfram 语言在舍入时总是尽量保持结果的有效性.
明确显示 Wolfram 语言为机器精度数 0. 处理的区间：
显示围绕 100. 的区间移动到0的结果：
建立这样的区间时，可以带有任何精度的数：
用普通机器精度算法，将给出不正确的结果：
生成的区间包含正确的0值：
不定结果和无穷结果
如果插入 0/0 这样的表达式，Wolfram 语言将显示一个信息返回结果 Indeterminate：
表达式 0/0 是一个不确定数值结果的例子. 如果用户打入0/0，Wolfram 语言没有办法知道你想要的答案. 如果通过取当 时 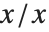的极限得到 0/0，那么你会想要结果为 1. 而取 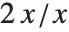的极限所得 0/0，那么你可能想要结果为 2. 表达式 0/0 本身没有含区别不同情况的足够信息. 因此其值必定是不确定的.
当一个不定结果产生时，Wolfram 语言就显示一个警告信息，然后返回 Indeterminate 作为结果. 如果在一个算术计算中使用 Indeterminate，那么总是得到结果 Indeterminate. 一个单个不定式将“毒害”任何算术运算. （符号Indeterminate 在 Wolfram 语言中所起的作用类似于IEEE浮点标准中的“非数”对象.）
通常的算术法则在 Indeterminate 情况下失效：
Indeterminate “毒害”任何算术运算. 导致一个不确定的结果：
当在 Wolfram 语言程序中进行算术运算时，能区分是否在运算中生成不确定的结果常常是重要的. 通过使用在 "消息" 中讨论的函数 Check 检测是否有与不确定结果相关的警告信息生成，可以实现这一点.
可在程序内使用 Check 来检测是否在计算中有警告：
Indeterminate
不确定的数值结果
Infinity
正无穷大量
-Infinity
负无穷大量 ( DirectedInfinity[-1] )
DirectedInfinity[r]
具有复方向 r 的无穷大量
ComplexInfinity
不定方向的无穷大量
DirectedInfinity[]
等价于 ComplexInfinity
不确定和无穷大量.
在许多场合下，能够用无穷大量做运算常常是方便的. 在 Wolfram 语言中符号 Infinity 代表正无穷大量，用户可使用其指明和式与积分上下限等，也可以用来做某些算术运算.
具有无穷大上限的积分：
Wolfram 语言知道 ：
如果试图求两个无穷大量的差，将得到不确定结果：
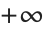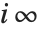在处理无穷大量中会出现许多微妙之处. 其中之一涉及到无穷大量的方向. 当计算无穷积分时，典型地考虑沿着复平面上某个趋向无穷大的路径进行积分. 在这种情况下，区分复平面上不同方向上的无穷大是重要的. 和 是两个例子，但在某些情况下，也需要 等等.
在 Wolfram 语言中，无穷大量可以有“方向”，其由一个复数来说明. 当键入符号 Infinity，代表正无穷大量，其内部被转换成 DirectedInfinity[1]， 该式代表 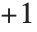方向上的无穷大量. 类似地，-Infinity 变成DirectedInfinity[-1]，IInfinity 变成 DirectedInfinity[I]. 尽管 DirectedInfinity 形式总是在内部使用，但 DirectedInfinity[r] 的标准输出格式是 r Infinity.
Infinity 在内部被转换成 DirectedInfinity[1]：
尽管“有向无穷大”的表示常常被使用，但并不总是有效的. 如果打入 1/0，将得到一个无穷大，但根本无法确定无穷大的方向. Wolfram 语言把 1/0 的结果表示为 DirectedInfinity[]. 在标准输出格式中，方向不定的无穷大被显示为ComplexInfinity.
1/0 给出一个方向不定的无穷大：
控制数值运算
NHoldAll
防止函数中的任何自变量被 N 影响
NHoldFirst
防止第一个参数被影响
NHoldRest
防止除第一个参数以外的任何参数被影响
用于控制数值计算的属性.
通常 N 进入到函数内并用于每个参数：
告诉 Wolfram 语言不要将 N 用于 f 的第一个参数：
f 的第一个参数保留为精确形式：