FourierSinTransform

FourierSinTransform[expr,t,ω]

gives the symbolic Fourier sine transform of expr.

FourierSinTransform[expr,{t1,t2,…},{ω1,ω2,…}]

gives the multidimensional Fourier sine transform of expr.

Details and Options

  • The Fourier sine transform is a particular way of viewing the Fourier transform without the need for complex numbers or negative frequencies.
  • Joseph Fourier designed his famous transform using this and the Fourier cosine transform, and they are still used in applications like signal processing, statistics and image and video compression.
  • The Fourier sine transform of the time domain function 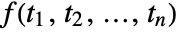is the frequency domain function 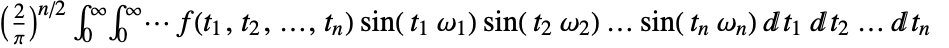for :
  • The Fourier sine transform of a function 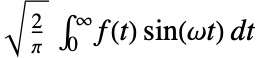is by default defined to be .
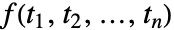  • The multidimensional Fourier sine transform of a function 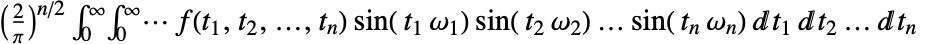is by default defined to be or when using vector notation, (2/pi)^(n/2)int_(t in TemplateBox[{}, PositiveReals]^n )f(t) sin(omega t)dt.
  • Different choices of definitions can be specified using the option FourierParameters.
  • The integral is computed using numerical methods if the third argument, 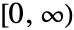, is given a numerical value.
  • The asymptotic Fourier sine transform can be computed using Asymptotic.
  • There are several related Fourier transformations:
  • FourierTransforminfinite continuous-time functions (FT)
    FourierSequenceTransforminfinite discrete-time functions (DTFT)
    FourierCoefficientfinite continuous-time functions (FS)
    Fourierfinite discrete-time functions (DFT)
  • The Fourier sine transform is an automorphism in the Schwartz vector space of functions whose derivatives are rapidly decreasing and thus induces an automorphism in its dual: the space of tempered distributions. These include absolutely integrable functions, well-behaved functions of polynomial growth and compactly supported distributions.
  • Hence, FourierSinTransform not only works with absolutely integrable functions on 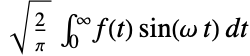, but it can also handle a variety of tempered distributions such as DiracDelta to enlarge the pool of functions or generalized functions it can effectively transform.
  • The following options can be given:
  • AccuracyGoal Automaticdigits of absolute accuracy sought
    Assumptions $Assumptionsassumptions to make about parameters
    FourierParameters {0,1}parameters to define the Fourier sine transform
    GenerateConditions Falsewhether to generate answers that involve conditions on parameters
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoal Automaticdigits of precision sought
    WorkingPrecision Automaticthe precision used in internal computations
  • Common settings for FourierParameters include:
  • {0,1}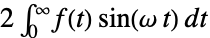
    {1,1}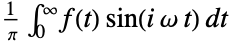
    {-1,1}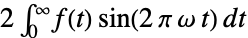
    {0,2Pi}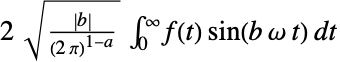
    {a,b}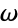

Examples

open allclose all

Basic Examples  (6)

Compute the Fourier sine transform of a function:

Plot the function and its Fourier sine transform:

Fourier sine transform of an exponential function:

For a different convention, change the parameters:

Fourier sine transform of the reciprocal of a square root:

Compute the Fourier sine transform of a multivariate function:

Plot the function and its transform:

Compute the transform at a single point:

Scope  (37)

Basic Uses  (3)

Fourier sine transform of a function for a symbolic parameter :

Plot the transform:

Fourier sine transforms involving trigonometric functions:

Plot the transform:

Plot the transform:

Evaluate the Fourier sine transform for a numerical value of the parameter :

Algebraic Functions  (3)

Fourier sine transform of power functions:

Sine transform of rational functions:

Plot the transform for :

Plot the transform for :

Transform when :

Plot the transform:

Plot the transform for :

Fourier sine transform of a quotient of two polynomials:

Plot the transform for:

Exponential and Logarithmic Functions  (3)

Fourier sine transforms for exponential functions:

Plot the transform for :

Plot the transform for :

Plot the transform:

Fourier sine transform of a Gaussian:

Transform when :

Plot the transform:

Plot the transform for :

Sine transforms of logarithmic functions:

Plot the transform:

Plot the transform for :

Plot the transform for :

Plot the transform:

Trigonometric Functions  (3)

Composition of elementary functions:

Plot the transform for :

Plot the transform for :

Plot the transform for :

Plot the transform for :

Fourier sine transform of the product of exponential and trigonometric functions:

Plot the transform for , :

Plot the transform for , :

Fourier sine transforms of arctangent functions:

Plot the transform:

Plot the transform:

Special Functions  (8)

Fourier sine transforms of expressions involving the Sinc function:

Plot the transform:

Plot the transform:

Fourier sine transform of ExpIntegralEi:

Plot the transform:

Transform of Erf:

Plot the transform:

Transform of Erfc:

Plot the transform for :

Expression involving the SinIntegral:

Plot the transform:

CosIntegral:

Plot the transform for :

Sine transforms for BesselJ functions:

Plot the transform for :

Plot the transform for and :

Plot the transform for and :

Sine transforms for BesselY functions:

Plot the transform for :

Plot the transform for and :

Piecewise Functions and Distributions  (4)

Fourier sine transform of a piecewise function:

Restriction of a sine function to a half-period:

Triangular function:

Transforms in terms of FresnelS:

Plot the transform:

Plot the transform:

Periodic Functions  (2)

Fourier sine transform of sine:

Fourier sine transform of SquareWave:

Generalized Functions  (4)

Fourier sine transforms of expressions involving HeavisideTheta:

Fourier sine transforms involving DiracDelta:

Plot the transform:

Plot the transform:

Fourier sine transform involving HeavisideLambda:

Fourier sine transform involving HeavisidePi:

Multivariate Functions  (2)

Fourier sine transform of an exponential functions in two variables:

Plot of both:

Plot of both:

Fourier sine transform of product of exponential and SquareWave:

Formal Properties  (3)

Fourier sine transform of a first-order derivative:

Fourier sine transform of a second-order derivative:

Fourier sine transform threads itself over equations:

Numerical Evaluation  (2)

Calculate the Fourier sine transform at a single point:

Alternatively, calculate the Fourier sine transform symbolically:

Then evaluate it for specific value of :

Options  (8)

AccuracyGoal  (1)

The option AccuracyGoal sets the number of digits of accuracy:

With default settings:

Assumptions  (1)

Fourier sine transform of BesselJ is a piecewise function:

FourierParameters  (3)

Fourier sine transform for the unit box function with different parameters:

Use a nondefault setting for a different definition of the transform:

To get the inverse, use the same FourierParameters setting:

Set up your particular global choice of parameters once per session:

Restore defaults:

GenerateConditions  (1)

Use GenerateConditions True to get the parameter conditions necessary for the result to be valid:

PrecisionGoal  (1)

The option PrecisionGoal sets the relative tolerance in the integration:

With default settings:

WorkingPrecision  (1)

If a WorkingPrecision is specified, the computation is done at that working precision:

With default settings:

Applications  (4)

Ordinary Differential Equations  (1)

Consider the following ODE with initial condition :

Apply the Fourier sine transform to the ODE:

Solve for the transform:

Find the inverse Fourier sine transform with and :

Compare with DSolveValue:

Partial Differential Equations  (1)

Solve the infinite diffusion problem for , : with initial condition for and boundary condition for :

Fourier sine transform with respect to :

With and , solve this ODE:

Compute the inverse sine transform:

Compare with DSolveValue:

Consider the special case with and :

Evaluation of Integrals  (2)

Calculate the following definite integral for :

Compute the Fourier sine transform of an exponential function:

Apply the Fourier sine inversion formula:

Solve for the definite integral:

Compare with Integrate:

Calculate the following definite integral for :

Compute the Fourier sine transform of an exponential function:

Apply Parseval's identity:

Or equivalently:

Solve for the definite integral:

Compare with Integrate:

Properties & Relations  (4)

By default, the Fourier sine transform of is:

For , the definite integral becomes:

Compare with FourierSinTransform:

Use Asymptotic to compute an asymptotic approximation:

FourierSinTransform and InverseFourierSinTransform are mutual inverses:

Results from FourierSinTransform and FourierTransform differ by a factor of for odd functions:

The results differ by a factor of for ω>0:

Possible Issues  (1)

The result from an inverse Fourier sine transform may not have the same form as the original:

The Fourier sine transform may be given in terms of generalized functions such as DiracDelta:

Neat Examples  (2)

The Fourier sine transform represented in terms of MeijerG:

Create a table of basic Fourier sine transforms:

Wolfram Research (1999), FourierSinTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierSinTransform.html (updated 2025).

Text

Wolfram Research (1999), FourierSinTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierSinTransform.html (updated 2025).

CMS

Wolfram Language. 1999. "FourierSinTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/FourierSinTransform.html.

APA

Wolfram Language. (1999). FourierSinTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierSinTransform.html

BibTeX

@misc{reference.wolfram_2024_fouriersintransform, author="Wolfram Research", title="{FourierSinTransform}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FourierSinTransform.html}", note=[Accessed: 15-January-2025 ]}

BibLaTeX

@online{reference.wolfram_2024_fouriersintransform, organization={Wolfram Research}, title={FourierSinTransform}, year={2025}, url={https://reference.wolfram.com/language/ref/FourierSinTransform.html}, note=[Accessed: 15-January-2025 ]}