





D 
詳細とオプション




- Dは一変量関数の微分としても知られている.
- 記号 ∂ を使い,
 pd
pd または\[PartialD]として下付き文字を付けて,以下のように微分を入力することができる.
または\[PartialD]として下付き文字を付けて,以下のように微分を入力することができる. -
D[f,x] ∂xf D[f,{x,n}] ∂{x,n}f D[f,x,y] ∂x,yf D[f,{{x,y}}] ∂{{x,y}}f - \[InvisibleComma]あるいは
 ,
, を使うとコンマが不可視にできる.
を使うとコンマが不可視にできる. - 偏微分D[f[x],x]は
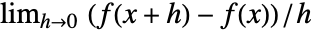 で定義できる.高次の微分D[f[x,y],x,y]は再帰的に
で定義できる.高次の微分D[f[x,y],x,y]は再帰的に 等で定義できる.
等で定義できる. - 微分係数 n および m の次数は記号的なもので,正の整数であると仮定される.
- 記号的な f についての微分D[f[x],{x,n}]はDerivative[n][f][x]として表すことができる.
- ある関数 f についてDerivative[n][f][x]が未知であることもあるが,Nを適用して近似することは可能である. »
- Derivative[n][f][x]の値を加えることで新たな微分規則を加えることができる. »
- リストについては,D[{f1,f2,…},x]は再帰的に{D[f1,x],D[f2,x],…}に等しい. »
- D[f,{array}]は,事実上,array の各要素をDに縫い込む.
- D[f,{array,n}]はD[f,{array},{array},…]に等しい.ただし,{array}は n 回繰り返されるものとする.
- D[f,{array1},{array2},…]は,通常は,First[Outer[D,{f},array1,array2,…]]に等しい. »
- 一般的な配列の微分には以下がある.
-
D[f,{{x1,x2,…}}] 勾配 {D[f,x1],D[f,x2],…} D[f,{{x1,x2,…},2}] ヘッセ {{D[f,x1,x1],D[f,x1,x2],…},{D[f,x2,x1],D[f,x2,x2],…},…} D[{f1,f2,…},{{x1,x2,…}}] ヤコビ {{D[f1,x1],D[f1,x2],…},
{D[f2,x1],D[f2,x2],…},…} - f がスカラーで x={x1,…}のとき,x0={x01,…}における多変量テイラー(Taylor)級数は以下で与えられる.
-
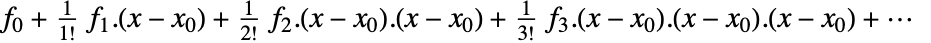
- ただし,fi=D[f,{x,i}]/.{x1x01,…}はテンソル階数
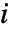 の配列である. »
の配列である. » - f と x が両方とも配列のとき,D[f,{x}]は最初に f の各要素に縫い込まれ,次に x の各要素に縫い込まれる.結果は次元がJoin[Dimensions[f],Dimensions[x]]の配列である. »
- VectorSymbol,MatrixSymbolあるいはArraySymbolを使って,変数あるいは関数の値が,ベクトル,行列,あるいは配列であることを示すことができる.
- Dは,範囲を区切られた変数や特定の演算子の構造を考慮しつつ積分や総和の演算子を形式的に微分する.
- 演算子の微分例
-
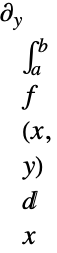
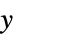 は積分によって範囲を区切られていない
は積分によって範囲を区切られていない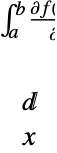
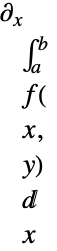
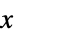 は積分によって範囲を区切られている
は積分によって範囲を区切られている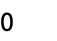
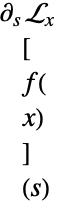
 は積分変換によって範囲を区切られていない
は積分変換によって範囲を区切られていない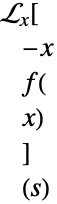
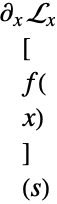
 は積分変換によって範囲を区切られている
は積分変換によって範囲を区切られている
- 与えられた変数に明示的に依存しない式はどれもゼロ偏微分を持つとみなされる.
- NonConstants{u1,…}の設定は ui が x, y, 等のすべての変数に依存し,ゼロ偏微分を持たないように指定する. »
例題
すべて開く すべて閉じる例 (7)
スコープ (89)
基本的な用法 (12)
記号関数 (9)
Inactive微分を使って規則を述べる:
初等関数 (6)
特殊関数 (8)
エアリー関数の微分は,AiryAiPrimeおよびAiryBiPrimeによって与えられる:
Zetaの微分は,原点において閉形の式を持つ:
JacobiSNの微分:
JacobiCDの微分:
LogIntegralの微分:
ExpIntegralEiの微分:
SinIntegralについての次数の n の微分:
ベクトル値関数 (5)
SparseArrayとして保存されてたベクトル値関数の微分:
SymmetrizedArrayタイプの構造配列オブジェクトとして表された行列の微分:
ベクトル引数の関数 (6)
SparseArrayとして保存されたベクトル値関数の勾配:
結果は非零の項だけを含む別のSparseArrayである:
SparseArrayとして計算されたヘッシアン:
勾配はSparseArrayとして計算することもできるが,その場合は事実上密行列になる:
SparseArrayとして計算されたヤコビアン:
記号配列の引数と関数 (8)
積分と積分変換 (6)
積分のInactive形式を微分して微積分の基本定理を得る:
非アクティブなFourierTransformを微分する:
総和と総和変換 (4)
総和のInactiveな形を微分する:
非アクティブなGeneratingFunctionを微分する:
指標付き微分 (9)
KroneckerDelta因子を含む指標付き変数について微分する:
Inactiveを使って総和の展開を阻止する:
総和因子は,名前が曖昧になるのを防ぐために,必要であれば名前が変えられる:
微分で定義される関数 (5)
Derivativeで偏微分を定義する:
アプリケーション (47)
微分の幾何学 (5)
多変量微分とベクトル微分 (6)
二次微分検定から,最初の2点(プロット中の赤と青)は極小値で,3番目の点(プロット中の緑)は鞍点である:
ArcCurvatureを使って同じ結果を得る:
平面上のベクトル場の回転は,その成分の微分を引くことで計算できる:
2D回転をある点におけるベクトル場の「回転」の展開図として可視化する.赤と緑はそれぞれ時計回りと反時計回りの回転と回転の大きさに比例した半径を表す:
ベクトル場の発散は,その成分の微分の総和を求めることで計算できる:
2Dの発散を,ある点におけるベクトル場のフローの展開図として可視化する.赤と緑はそれぞれ出て行く流れと入ってくる流れを表す.半径はフローの大きさに比例する:
微分方程式 (6)
変化率 (5)
隠関数 (3)
ロピタルの定理 (3)
記号配列微分 (6)
第2導関数は ![]() には依存しないので,二次近似は厳密値に等しい:
には依存しないので,二次近似は厳密値に等しい:
ペア![]() のリストとして与えられたデータ
のリストとして与えられたデータ ![]() についての最小二乗解を導出する:
についての最小二乗解を導出する:
最尤法を使って与えられたデータの最良フィットを与えるGammaDistributionパラメータを求める:
EstimatedDistributionを使って計算した結果と比較する:
期待収益 ![]() ,標準偏差
,標準偏差 ![]() の場合のポートフォリオの最適化問題の最適条件を求める:
の場合のポートフォリオの最適化問題の最適条件を求める:
目標は,資産重みのベクトル ![]() がTotal[x]=1を満たすときに,
がTotal[x]=1を満たすときに,![]() を最大化することである.製薬条件を使って,制約のないベクトル変数
を最大化することである.製薬条件を使って,制約のないベクトル変数 ![]() が
が ![]() の最初の
の最初の ![]() 個の座標で構成される
個の座標で構成される ![]() を表すことができる:
を表すことができる:
方程式 ![]() で表される線形回帰モデルの対数尤度関数の勾配を計算する.
で表される線形回帰モデルの対数尤度関数の勾配を計算する.![]() は,正規分布に従う,平均が0で偏差が
は,正規分布に従う,平均が0で偏差が ![]() のランダム変数である:
のランダム変数である:
特性と関係 (23)
DifferenceQuotientのLimitは微分Dである:
Integrate内の微分:
Dは形式的な結果をDerivativeによって返す:
Dは式を与えられた変数について微分する:
Derivativeは演算子で純関数の結果を返す:
微分の近似にはNを使う:
D[f,{array1},…]は,事実上First[Outer[D,{f},array1,…]]に等しい:
f と a が配列なら,Dimensions[D[f,{a}]]==Join[Dimensions[f],Dimensions[a]]である:
D[f,{{x1,x2,…,xn}}]は,事実上Grad[f,{x1,x2,…,xn}]に等しい:
Div[{f1,f2,…,fn},{x1,x2,…,xn}]は f のベクトル微分のトレースである:
より一般的には,Div[f,x]は f のベクトル微分の最後の2次元を簡約したものである:
Curl[f,x]は f のベクトル微分のHodgeDualに![]() をかけたものである.ただし,r は f の階数である:
をかけたものである.ただし,r は f の階数である:
スカラー f については,Laplacian[f,{x1,x2,…,xn}]は f の二次ベクトル微分のトレースである:
より一般的には,Laplacian[f,x]は f の二次ベクトル微分の最後の2次元を簡約したものである:
Total[a]の a についての導関数を記号配列を使って計算する:
ArcCurvatureはDによって定義することができる:
Dを使って同次ディリクレ境界条件がある熱伝導方程式を指定する:
この微分系の固有系はDEigensystemで求めることができる:
DはDifferenceDeltaを使って定義することができる:
DはDiscreteShiftを使って定義することができる:
Dは,他の変数が微分変数からは独立であると仮定する:
Dtは,他の変数が微分変数に依存するかもしれないと仮定する:
手作業で他の変数をすべて定数として指定すると,DtもDと同じ結果を返す:
ImplicitDを使って陰関数の導関数を計算する:
考えられる問題 (5)
関連項目
Dt Derivative DifferenceQuotient Minimize Maximize DSolve NDSolve NDEigensystem NDEigenvalues Integrate Grad Div Curl Laplacian DifferenceDelta CoefficientArrays FractionalD CaputoD ImplicitD
Function Repository: NDerivative FractionalD ListD JacobianMatrix ChainD ProductD FiniteDifferenceStencil
テクニカルノート
-
▪
- 記号数学:基本操作 ▪
- 導関数の表し方 ▪
- 未知の関数の導関数 ▪
- 実装に関するノート: 代数と解析
関連するガイド
-
▪
- 微積分 ▪
- 中学・高校における教育 ▪
- 記号的なベクトル,行列,配列 ▪
- 偏微分方程式 ▪
- 微分方程式
関連リンク
履歴
1988 で導入 (1.0) | 1996 で更新 (3.0) ▪ 2004 (5.1) ▪ 2008 (7.0) ▪ 2017 (11.1) ▪ 2024 (14.1)
テキスト
Wolfram Research (1988), D, Wolfram言語関数, https://reference.wolfram.com/language/ref/D.html (2024年に更新).
CMS
Wolfram Language. 1988. "D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/D.html.
APA
Wolfram Language. (1988). D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/D.html
BibTeX
@misc{reference.wolfram_2025_d, author="Wolfram Research", title="{D}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/D.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_d, organization={Wolfram Research}, title={D}, year={2024}, url={https://reference.wolfram.com/language/ref/D.html}, note=[Accessed: 05-February-2026]}