D 
D[f,x]
给出偏导数 ![]() .
.
D[f,{x,n}]
给出高阶导数 ![]() .
.
D[f,x,y,…]
给出偏导数 ![]() .
.
D[f,{x,n},{y,m},…]
给出高阶偏导数 ![]() .
.
D[f,{{x1,x2,…}}]
给出标量 f 的向量导数 ![]() .
.
D[f,{array}]
给出数组导数.
更多信息和选项




- D 也被称作一元函数的导数.
- 通过
 pd
pd 或 \[PartialD] 输入字符 ∂ 以及下标,导数的输入方式如下:
或 \[PartialD] 输入字符 ∂ 以及下标,导数的输入方式如下: -
D[f,x] ∂xf D[f,{x,n}] ∂{x,n}f D[f,x,y] ∂x,yf D[f,{{x,y}}] ∂{{x,y}}f - 通过使用字符 \[InvisibleComma] 或
 ,
, ,可以使逗号不可见.
,可以使逗号不可见. - 偏导数 D[f[x],x] 可以用
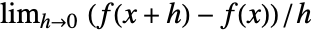 定义,高阶导数 D[f[x,y],x,y] 可以用
定义,高阶导数 D[f[x,y],x,y] 可以用 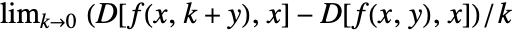 等递归地定义.
等递归地定义. - 导数的阶数 n 和 m 可以是符号,并被认为是正整数.
- 符号 f 的导数 D[f[x],{x,n}] 表示为 Derivative[n][f][x].
- 对于有些函数 f,Derivative[n][f][x] 可能是未知的,但可以通过应用 N 逼近. »
- 新的导数规则可以通过对 Derivative[n][f][x] 添加值来添加. »
- 对于列表,D[{f1,f2,…},x] 等价于递归式地进行 {D[f1,x],D[f2,x],…}. »
- D[f,{array}] 实际上会将 D 逐项作用于 array 的每个元素.
- D[f,{array,n}] 等价于 D[f,{array},{array},…],其中 {array} 被重复 n 次.
- D[f,{array1},{array2},…] 通常等价于 First[Outer[D,{f},array1,array2,…]]. »
- 常见的数组导数包括:
-
D[f,{{x1,x2,…}}] 梯度 {D[f,x1],D[f,x2],…} D[f,{{x1,x2,…},2}] 海森 {{D[f,x1,x1],D[f,x1,x2],…},{D[f,x2,x1],D[f,x2,x2],…},…} D[{f1,f2,…},{{x1,x2,…}}] 雅可比 {{D[f1,x1],D[f1,x2],…},
{D[f2,x1],D[f2,x2],…},…} - 如果 f 为标量且 x={x1,…},则在 x0={x01,…} 处的多元泰勒级数可以表示为:
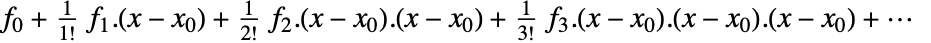 ,
,- 其中 fi=D[f,{x,i}]/.{x1x01,…} 是一个张量秩为
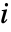 的数组. »
的数组. » - 如果 f 和 x 均为数组,则 D[f,{x}] 实际上会先逐项作用于 f 的各个元素,然后再逐项作用于 x 的各个元素. 结果是维数为 Join[Dimensions[f],Dimensions[x]] 的数组. »
- VectorSymbol、MatrixSymbol 或 ArraySymbol 可用于表示变量或函数值是向量、矩阵或数组.
- D 可以正式地对积分和求和之类的算符进行求导,考虑到作用域受限的变量以及特殊算符的结构.
- 算符导数的范例包括:
-
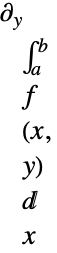
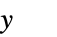 不受积分限制
不受积分限制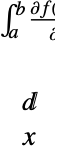
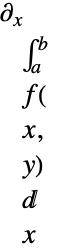
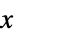 受限于积分
受限于积分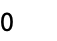
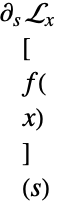
 不受积分变换限制
不受积分变换限制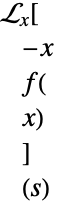
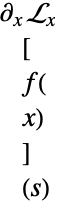
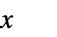 受限于积分变换
受限于积分变换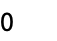
- 认为所有不显式依赖已知变量的表达式具有零偏导.
- 设置 NonConstants{u1,…} 指定 ui 依赖于所有变量 x、y 等,并且不具有零偏导数. »
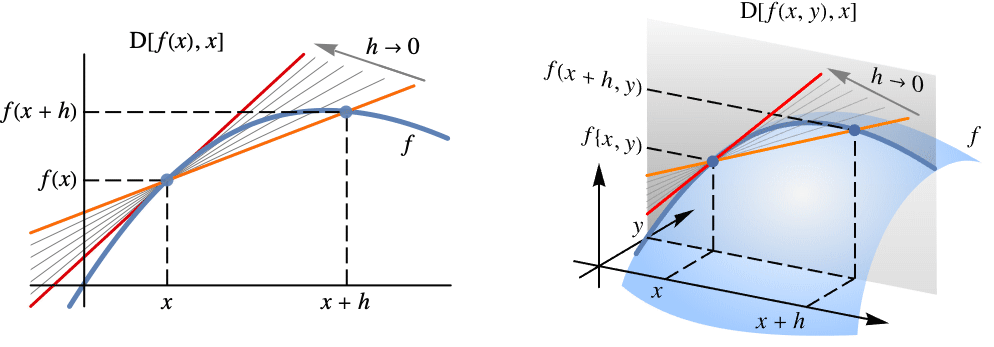
范例
打开所有单元关闭所有单元范围 (89)
基本用法 (12)
符号函数 (9)
使用 Inactive 导数表明规则:
初级函数 (6)
特殊函数 (8)
艾里函数的导数以 AiryAiPrime 和 AiryBiPrime 的形式给出:
Zeta 的导数在原点处具有解析形式表达式:
JacobiSN 的导数:
JacobiCD 的导数:
LogIntegral 的导数:
ExpIntegralEi 的导数:
SinIntegral 的 n 阶导数:
矢量值函数 (5)
存储为 SparseArray 的向量值函数的导数:
用 SymmetrizedArray 对象表示矩阵的导数:
向量参数函数 (6)
存储为 SparseArray 的向量值函数的梯度:
结果也是一个 SparseArray,仅含有非零项:
作为 SparseArray 计算的海森行列式:
梯度也可以作为 SparseArray 计算,但在此例中它实际上是稠密的:
以 SparseArray 计算雅可比行列式:
符号数组参数和函数 (8)
积分和积分变换 (6)
对积分的 Inactive 形式求导,得到积分的基本定理:
对未激活的 FourierTransform 求导:
求和和与求和变换 (4)
索引微分 (9)
对带有下标的变量微分,引入 KroneckerDelta 因子:
使用 Inactive 防止和式的展开:
导数定义的函数 (5)
应用 (47)
导数的几何表示 (5)
函数特征 (5)
多变量和向量微积分 (6)
根据二阶导数检测,头两个点(在图形中用红色和蓝色表示)为极小值点,第三个点(绿色)为鞍点:
使用 ArcCurvature 得到相同结果:
微分方程 (6)
隐函数 (3)
符号数组微积分 (6)
使用最大似然法求得最拟合给定数据的 GammaDistribution 参数:
与使用 EstimatedDistribution 计算出的结果进行比较:
为预期收益率为 ![]() 、标准差为
、标准差为 ![]() 的投资组合优化问题找出最优条件:
的投资组合优化问题找出最优条件:
当资产权重向量 ![]() 满足 Total[x]=1 时,目标是最大化
满足 Total[x]=1 时,目标是最大化 ![]() . 该约束可以用来表示
. 该约束可以用来表示 ![]() ,其中无约束向量变量
,其中无约束向量变量 ![]() 由
由 ![]() 的前
的前 ![]() 个坐标组成:
个坐标组成:
属性和关系 (23)
DifferenceQuotient 的 Limit 是导数 D:
Integrate 内部的微分:
D 返回以 Derivative 表示的正式结果:
D 关于已知变量对表达式求导:
Derivative 是一个算符,返回纯函数结果:
可以使用 N 获得导数的逼近值:
D[f,{array1},…] 实际上等价于 First[Outer[D,{f},array1,…]]:
如果 f 和 a 为数组,Dimensions[D[f,{a}]==Join[Dimensions[f],Dimensions[a]]:
D[f,{{x1,x2,…,xn}}] 实际上等价于 Grad[f,{x1,x2,…,xn}]:
Div[{f1,f2,…,fn},{x1,x2,…,xn}] 是 f 的向量导数的迹:
更一般地,Div[f,x] 是 f 的向量导数后两个维数的缩并:
Curl[f,x] 是 ![]() 乘以 f 的向量导数的 HodgeDual,其中 r 是 f 的秩:
乘以 f 的向量导数的 HodgeDual,其中 r 是 f 的秩:
对于标量 f,Laplacian[f,{x1,x2,…,xn}] 是 f 的二阶向量导数的迹:
更一般地,Laplacian[f,x] 是 f 的二阶向量导数后两个维数的缩并:
使用符号数组计算 Total[a] 关于 a 的导数:
ArcCurvature 可以定义为 D 的形式:
使用 D 指定具有齐次狄利克雷边界条件的热方程:
此微分系统的特征系统可以通过 DEigensystem 得到:
D 可以使用 DifferenceDelta 定义:
D 可以使用 DiscreteShift 定义:
D 假定其他变量独立于微分变量:
Dt 假定其他变量可以取决于微分变量:
通过手动指定所有其它变量为常数,Dt 可以得到与 D 相同的结果:
使用 ImplicitD 计算隐函数的导数:
可能存在的问题 (5)
文本
Wolfram Research (1988),D,Wolfram 语言函数,https://reference.wolfram.com/language/ref/D.html (更新于 2024 年).
CMS
Wolfram 语言. 1988. "D." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/D.html.
APA
Wolfram 语言. (1988). D. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/D.html 年