MeshRegion

MeshRegion[{p1,p2,…},{mcell1[{i1,…}],mcell2[{j1,…}],…}]

セル mcelljを持つメッシュを与える．ただし，整数 i として与えられる座標は piであるとみなされる．

MeshRegion[…,{…,wi[mcelli[…]],…}]

セルの特性が記号ラッパー wiで定義されたメッシュを与える．

MeshRegion[mreg,opts]

メッシュ領域 mreg からオプション opts のメッシュを与える．

詳細とオプション

  • MeshRegionは，単体的複体あるいは胞複体としても知られている．
  • MeshRegionは，次元1，2あるいは3に埋め込まれた任意の幾何次元の区分線形領域を表すことができる．
  • MeshRegion[…]は，ノートブック中に，メッシュ領域のプロットとして表示される．
  • MeshRegionは，一般に，DelaunayMesh，DiscretizeGraphics，DiscretizeRegion等の関数を使って作られる．
  • MeshRegionで表される領域は，メッシュセルの非交和からなる．
  • MeshRegionは，各点 piの長さと等しく，RegionEmbeddingDimensionを使って求めることができる，埋込み次元を持つ．
  • 各セルは幾何次元を持ち，RegionDimensionを使って求めることができる．
  • 可能なメッシュセル mcelliとその幾何次元
  • Point[i]0点
    Line[{i1,i2,…}]1線分 {i1,i2}, {i2,i3}, …
    Triangle[{i1,i2,i3}]2塗り潰された三角形
    Polygon[{i1,i2,…}]2塗り潰された多角形
    Polyhedron[{{ii,i2,…},…}]3塗り潰された多面体
    Tetrahedron[{i1,…,i4}]3塗り潰された四面体
    Hexahedron[{i1,…,i8}]3塗り潰された六面体
    Pyramid[{i1,…,i5}]3塗り潰された角錐
    Prism[{i1,…,i6}]3塗り潰された角柱
    Simplex[{i1,…,ik}]0, 1, 2, 3塗り潰されたシンプレックス
  • Tetrahedron，Hexahedron，Pyramid，およびPrismは，3D座標でのみ使うことができる．
  • Point，Line，Triangle，Polygon，Polyhedron，Tetrahedron，Hexahedron，Pyramid，Prism，Simplexはどれも，複数のセル指定をも持っている．
  • 次の特別ラッパー wiをセルに使うことができる．
  • Labeled[cell,…]cell にラベルを付けて表示する
    Style[cell,…]cell を指定のスタイルで示す
    Annotation[cell,namevalue]注釈 name->value を cell に関連付ける
  • MeshRegion中の各セルは，{d,i}の形式の一意的なMeshCellIndexを与えられる．d は幾何次元，i は指標である．
  • MeshRegionのセルを選ぶ目的のために，次のセル指定を使うことができる．
  • {d,i}次元 d の指標 i のセル
    {d,ispec}次元 d の指標指定 ispec のセル
    {dspec,…}dspec で与えられる次元のセル
    h[{i1,…}]頭部 h，頂点指標 i1, …の明示的なセル
    {c1,c2,…}明示的なセル ciのリスト
  • 指標指定 ispec は次の形でよい．
  • iセル指標 i
    {i1,i2,…}指標 ikのセル
    Allすべてのセル
    pattパターン patt にマッチする指標のセル
  • 次元指定 dspec は次の形でよい．
  • d明示的な次元 d
    All0から領域の幾何次元までのすべての次元
    pattパターン patt にマッチする次元
  • MeshRegionは，常に，最適化された表現に変換され，AtomQのような関数とパターンマッチの目的では生のものとして扱われる．
  • MeshRegionには，埋込み次元2についてはGraphics，埋込み次元3についてはGraphics3Dのオプションと同じものに以下の追加・訂正を加えたものが使える．
  • MeshCellLabel Automaticセルのラベルと置き方
    MeshCellShapeFunction Automaticセルの形状関数
    MeshCellStyle Automaticセルのスタイル
    MeshCellHighlight {}ハイライトされたセルのリスト
    MeshCellMarker 0セルの整数マーカー
    PlotTheme $PlotThemeメッシュの全体的なテーマ
  • PlotThemeの可能な設定には，共通の基本テーマ，フォントの特徴のテーマ，サイズの特徴のテーマがある．
  • メッシュの特徴のテーマはメッシュセルのプロットに影響する．テーマには次のよのうなものがある．
  • "Points"0Dセル
    "Lines"1Dセル，ワイヤーフレーム
    "Polygons"2Dセル
  • 特徴のテーマの描画はメッシュの描画に影響する．テーマには次のよのうなものがある．
  • "SampledPoints"メッシュセルからサンプルされた点
    "SphereAndTube"曲面としての点と円筒としての線
    "SmoothShading"平滑化陰影付け
    "FaceNormals"各2Dセルの法線
    "LargeMesh"多数のセルについて最適化
  • セルのスタイルその他の指定は，事実上，MeshCellStyle，Styleその他のラッパーの順に適用される．後の指定は先の指定を無効にする．
  • セルラベルのスタイルその他の指定は，事実上，MeshCellLabel，Labeledの順に適用される．後の指定は先の指定を無効にする．
  • MeshRegionはRegionMember，RegionDistance，RegionMeasure，NIntegrate等の関数で使うことができる．

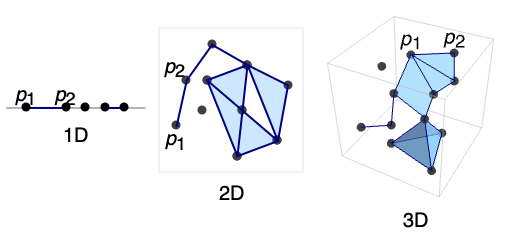
例題

すべて開くすべて閉じる

例  (6)

1Dにおける1D（曲線）メッシュ領域：

各点にその指標でラベルを付ける：

2Dにおける1D（曲線）メッシュ領域：

各点にその指標でラベルを付ける：

各点にその指標でラベルが付いた，3Dにおける2D（曲面）メッシュ領域：

各点にその指標でラベルが付いた，3Dにおける3D（立体）メッシュ領域：

いろいろな次元のセルを含むメッシュ領域：

DelaunayMeshからの3Dの立体メッシュ領域：

体積を求める：

スコープ  (41)

1D領域  (3)

厳密に0DのMeshRegionは点の集合である：

点にHighlightMeshでラベルを付ける：

厳密に1DのMeshRegionは線分の集合である：

線分にHighlightMeshでラベルを付ける：

MeshRegionは，次元が異なる要素を組み合せることができる：

DimensionalMeshComponentsでそれぞれに分割する：

2D領域  (4)

厳密に0DのMeshRegionは点の集合である：

点にHighlightMeshでラベルを付ける：

厳密に1DのMeshRegionは線分の集合である：

線分にHighlightMeshでラベルを付ける：

厳密に2DのMeshRegionは多角形の面の集合である：

面にHighlightMeshでラベルを付ける：

MeshRegionは，次元が異なる要素を組み合せることができる：

DimensionalMeshComponentsでそれぞれに分割する：

3D領域  (5)

厳密に0DのMeshRegionは点の集合である：

点にHighlightMeshでラベルを付ける：

厳密に1DのMeshRegionは線分の集合である：

線分にHighlightMeshでラベルを付ける：

厳密に2DのMeshRegionは多角形の面の集合である：

面にHighlightMeshでラベルを付ける：

厳密に3DのMeshRegionは多面体立体の集合である：

多面体立体のセルにはTetrahedron，Prism，Pyramid，Hexahedronが含まれる：

MeshRegionは次元が異なる要素を組み合せることができる：

プレゼンテーション  (11)

MeshCellLabelを使ってMeshRegionの一部にラベルを付けることができる：

ラベルは文字列ではなくてもよい：

Labeledをラッパーとして使い，MeshRegionを構築するときにセルにラベルを付けることができる：

ラベルは文字列ではなくてもよい：

MeshCellMarkerを使ってMeshRegionの一部に印を付けることができる：

MeshCellStyleを使ってMeshRegionの成分のStyleを設定することができる：

Styleをラッパーとして使い，MeshRegionを構築する際にセルにスタイルを付けることができる：

テーマを使って0Dセルを描く：

テーマを使って1Dセルあるいはワイヤーフレームを描く：

テーマを使って2Dセルを描く：

テーマを使ってメッシュセルからサンプルされた点を描く：

テーマを使って陰影付けを滑らかにする：

テーマを使って各2Dセルの法線を描く：

領域の特性  (8)

埋込み次元：

幾何次元：

点の帰属判定：

これを可視化する：

測度は1DメッシュではArcLength，2DメッシュではArea，3DメッシュではVolumeである：

それぞれの重心を計算し，可視化する：

点からの距離：

これを可視化する：

点からの符号付き距離：

これを可視化する：

領域内の最近点：

これを可視化する：

MeshRegionは常に有界である：

境界を得る：

境界ボックスを可視化する：

MeshRegion上でのIntegrate：

メッシュ領域  (10)

MeshCellCountは，指定された次元あるいはセル指定にマッチするセルの数を返す：

1Dセルの数を得る：

セル指定が与えられていない場合は，各次元の値が返される：

MeshCellsは，指定された次元あるいはセル指定にマッチしたメッシュ中のセルを返す：

1Dセルを得る：

個別のセル指標あるいはセル指標の集合を使うことができる：

MeshCellIndexは，メッシュ中のセルあるいはセル集合の指標を得る：

MeshCoordinatesは，メッシュの座標を得る：

座標のリストはMeshCellsが参照するものである：

MeshPrimitivesは，メッシュを構成しているプリミティブを返す：

個別のセル指標あるいはセル指標の集合を使うことができる：

DimensionalMeshComponentsは，メッシュ内の成分を次元ごとに分ける：

ConnectedMeshComponentsは，連結性に基づいてメッシュの成分を分ける：

MeshCellMeasureを使ってメッシュ中のセル集合の測度を得ることができる：

各次元に適切な測度が使われる：

MeshCellCentroidを使って，メッシュ中のセル集合の重心を得ることができる：

これを可視化する：

MeshCellQualityを使ってメッシュ中のセル集合の品質を得ることができる：

オプション  (114)

AlignmentPoint  (1)

座標を使って3D Insetで整列する位置を指定する：

AspectRatio  (1)

AspectRatioに数値を使う：

Axes  (2)

すべての軸を描く：

軸は描くが 軸は描かない：

AxesEdge  (2)

境界ボックスの辺を自動的に選択して軸を描く：

境界ボックスの辺を自動的に選んで軸を描く：

AxesLabel  (2)

軸にラベルを置く：

各軸にラベルを指定する：

AxesOrigin  (2)

どこで軸が交差するかを自動的に決定する：

軸の原点を明示的に指定する：

AxesStyle  (2)

目盛と目盛ラベルを含む，全体的な軸のスタイルを指定する：

各軸のスタイルを指定する：

Background  (1)

背景色を指定する：

BaselinePosition  (3)

グラフィックスの中心とテキストのベースラインを揃える：

Scaledを使い，グラフィックスのベースラインを高さの割合として指定する：

グラフィックスの軸をベースラインとして使う：

BaseStyle  (2)

初期スタイルを設定する：

複数の初期スタイルを指定する：

Boxed  (2)

境界ボックスの辺を描く：

境界ボックスの辺は描かない：

BoxRatios  (2)

境界ボックスの辺の割合を指定する：

割合に実際の座標値を使う：

BoxStyle  (1)

境界ボックスに破線を使う：

Epilog  (1)

グラフィックスの上に軸も含めて円板を描く：

FaceGrids  (4)

3Dグラフィックスのすべての面に格子を置く：

‐ 面の両方に面格子を置く：

平面に面格子を置く：

平面上で，，，上に格子線を置く：

FaceGridsStyle  (1)

面格子の全体的なスタイルを指定する：

Frame  (2)

グラフィックス全体の周囲に枠を描く：

左右の辺に枠を描く：

FrameLabel  (2)

底と左の辺に枠ラベルを指定する：

各辺のラベルを指定する：

FrameStyle  (2)

全体的な枠スタイルを指定する：

各枠辺のスタイルを指定する：

FrameTicks  (3)

枠は置くが目盛は描かない：

底と左の枠辺に目盛マークのラベルを置く：

底と右の辺に枠目盛を置く：

FrameTicksStyle  (2)

枠目盛と枠目盛ラベルのスタイルを指定する：

各辺についての枠目盛のスタイルを指定する：

GridLines  (3)

2Dグラフィックスに格子を置く：

特定の場所に格子線を描く：

各格子のスタイルを指定する：

GridLinesStyle  (1)

全体的な格子スタイルを指定する：

ImageMargins  (3)

ImageSizeの外側に余白を置かない：

すべての側に20ポイントの余白を置く：

特定の場所に格子線を描く：

ImagePadding  (4)

プロット範囲の外側に充填しない：

存在するすべてのオブジェクトとラベルに十分な充填を行う：

すべての側に印刷用ポイント数で同じ充填を指定する：

すべての側に印刷用ポイント数で同じ充填を指定する：

ImageSize  (3)

定義済みの記号サイズを使う：

明示的な画像幅を使う：

画像の明示的な幅と高さを使う：

LabelStyle  (1)

すべてのラベル様の要素の全体的なスタイルを指定する：

Lighting  (4)

周辺照明はその場にあるすべての表面に一様に適用される：

色の異なる指向性ライト：

色の異なるポイントライト：

色の異なるスポットライト：

MeshCellHighlight  (3)

MeshCellHighlightでは，MeshRegionの部分的なハイライトを指定することができる：

面を透過的にすることで3D MeshRegionの内部構造を見ることができる：

個々のセルはセル指標を使ってハイライトすることができる：

セル自体でもハイライトできる：

MeshCellLabel  (3)

MeshCellLabelを使ってMeshRegionの各部分にラベルを付けることができる：

多角形の頂点と辺にラベルを付ける：

セル指標を使って個々のセルにラベルを付けることができる：

セルそれ自身を使うこともできる：

MeshCellMarker  (1)

MeshCellMarkerを使ってMeshRegionの部分に値を割り当てることができる：

MeshCellLabelを使ってマーカーを示す：

MeshCellShapeFunction  (2)

MeshCellShapeFunctionは，MeshRegionの部分についての関数を指定することができる：

個々のセルはセル指標を使って描画することができる：

セル自体を使うこともできる：

MeshCellStyle  (3)

MeshCellStyleを使うと，MeshRegionの部分のスタイルを指定することができる：

面を透過的にすることで，3DMeshRegionの内部構造が見えるようになる：

個々のセルに，それ自身のセル指標を使ってスタイル付けすることができる：

セル自体を使うこともできる：

PlotLabel  (2)

TraditionalForm中のグラフィックスの上にラベルを表示する：

Styleおよび他のタイプセット関数を使ってラベルの見え方を変更する：

PlotRange  (3)

すべてのオブジェクトを表示する：

と の範囲を明示的に選択する：

PlotRangeでの切取りを強制する：

PlotRange -> s はPlotRange -> {{-s, s}, {-s, s}}に等しい：

PlotRangeClipping  (2)

グラフィックスオブジェクトがPlotRangeを超えて広がることを許す：

PlotRangeですべてのグラフィックスオブジェクトを切り取る：

PlotRangePadding  (3)

すべての側に1座標単位の充填を含む：

Scaled座標を使って充填を含む：

各側に別々の充填を指定する：

PlotRegion  (3)

グラフィックスのコンテンツは領域全体を使う：

グラフィックスのコンテンツを各方向に領域の真ん中半分に制限する：

ImagePaddingを使ってグラフィックスの周りに充填を加えることもできる：

PlotTheme  (9)

基本テーマ  (2)

一般的な基本テーマを使う：

白黒のテーマを使う：

特徴テーマ  (7)

テーマを使って0Dセルを描く：

テーマを使って1Dセルあるいはワイヤーフレームを描く：

テーマを使って2Dセルを描く：

テーマを使ってメッシュセルからサンプルされた点を描く：

テーマを使って，点を球，線を円筒として描く：

テーマを使って陰影付けを滑らかにする：

テーマを使って各2Dセルの法線を描く：

Prolog  (1)

背景として使う単純なグラフィックスを定義する：

これを多重メッシュ領域に使う：

RotateLabel  (2)

垂直枠のラベルを回転するように指定する：

垂直枠のラベルを回転しないように指定する：

SphericalRegion  (2)

連続する画像が，向きとは無関係に，一貫した大きさになるようにする：

SphericalRegionがないと，各画像は可能な限り大きくなる：

Ticks  (3)

軸は描くが目盛マークは描かない：

目盛マークを自動的に置く：

目盛マークを指定された場所に描く：

TicksStyle  (2)

目盛と目盛ラベルのスタイルを指定する：

軸と 軸の目盛のスタイルを別々に指定する：

ViewAngle  (1)

シミュレーションカメラのために特定の角度を使う：

ViewCenter  (1)

オブジェクトの右上のコーナーを最終画像の中心に置く：

ViewMatrix  (1)

負の の方向からのメッシュ領域の正投影ビュー：

ViewPoint  (3)

特別のスケールされた座標を使って視点を指定する：

記号による視点を使う：

正投影ビューを指定する：

ViewRange  (2)

デフォルトで，範囲はすべてのオブジェクトを含むのに十分になっている：

カメラからの最短および最長の距離を指定する：

ViewVector  (1)

通常の座標を使ってビューベクトルを指定する：

ViewVertical  (2)

最終画像で 軸方向を垂直方向として使う：

垂直方向のさまざまなビュー：

アプリケーション  (9)

曲線  (4)

MeshRegionから線を抽出し，ワイヤーフレームメッシュを作る：

MeshCellsで与えられる指標は，MeshCoordinatesに対応する：

特性を比較する：

正多角形の外周を計算する：

外周長を計算する：

辺の数が無限大に近付くにつれ，外周は に近付く：

L(Lindenmayer)システムを使ってコッホ(Koch)曲線のメッシュ領域を作る：

タートルグラフィックスを使って，座標に対する出力文字列内の文字を解釈するための関数を定義する：

出力文字列内を解釈するための初期パラメータ：

出力文字列内からコッホ曲線の座標を計算する：

座標からメッシュ領域を生成する：

反復 におけるコッホ曲線の長さの式を求める：

グラフをMeshRegionに変換する：

いくつかの2D埋込みグラフ：

これらを幾何学領域として計算に使うことができる：

いくつかの3D埋込みグラフ：

これらも計算に使うことができる：

例えば，これらの曲線に沿って曲線積分が計算できる：

曲面  (3)

2D曲線メッシュを押し出すことで曲面メッシュを作る：

平面レイアウトによるいくつかの例：

結果の領域を使って計算することができる．この場合は曲面積分が計算できる：

長方形の格子メッシュを直接生成する．ここではFlattenがするように，IndexFlattenが位置指標を平坦化する：

1Dメッシュの積として同じメッシュ領域を生成することもできる：

上記の直接法を一般化し，パターン行列に対応するメッシュ領域を生成する：

簡単なパターン：

より複雑なパターン：

立体  (2)

長方形格子メッシュを直接生成する．ここでは，Flattenがするのと同じように，IndexFlattenが位置指標を平坦化する：

同じメッシュ領域を1Dメッシュの積として生成することもできる：

上記の直接法を一般化して，パターン行列に対応するメッシュ領域を生成する：

簡単なパターン：

より複雑なパターン：

上記の考え方を使ってSeidelメッシュ，つまり，あらゆる方向にトンネルが通っていてしかも交差しないメッシュ領域を構築する：

境界メッシュに変換しスタイルを施すことで，理解が簡単になる：

特性と関係  (9)

MeshRegionは任意の幾何次元を持つことができる：

MeshRegionは常に有界である：

BoundedRegionQを使って調べ，RegionBoundsを使って実際の境界を調べる：

MeshRegionQを使って領域がMeshRegionかどうかを調べることができる：

DelaunayMeshを使って点の集合からMeshRegionを作る：

TriangulateMeshを使ってBoundaryMeshRegionをMeshRegionに変換する：

DiscretizeRegionを使って任意の領域をMeshRegionに変換する：

DiscretizeGraphicsを使ってGraphicsをMeshRegionに変換する：

Showを使って任意のMeshRegionをGraphicsに変換する：

MeshRegionは，BoundaryMeshRegionよりメモリを多く必要とすることが多い：

Wolfram Research (2014), MeshRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/MeshRegion.html （2022年に更新）.

テキスト

Wolfram Research (2014), MeshRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/MeshRegion.html （2022年に更新）.

CMS

Wolfram Language. 2014. "MeshRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/MeshRegion.html.

APA

Wolfram Language. (2014). MeshRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeshRegion.html

BibTeX

@misc{reference.wolfram_2024_meshregion, author="Wolfram Research", title="{MeshRegion}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/MeshRegion.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_meshregion, organization={Wolfram Research}, title={MeshRegion}, year={2022}, url={https://reference.wolfram.com/language/ref/MeshRegion.html}, note=[Accessed: 21-November-2024 ]}